31.Преобразование подобия.

Преобразование подобия. Говорят, что матрицы А и В подобны, если существует невырожденная матрица Р (матрица подобия) такая, что В = Р~1АР. Само преобразование матрицы А к виду В = Р~1АР называется преобразованием подобия. Преобразование подобия матрицы возникает естественным образом как результат замены переменных (или перехода к новому базису) в пространстве m-мерных векторов.

Важно то, что и полученная в результате преобразования подобия матрица имеет тот же набор собственных чисел.

32. Матрица Хессенберга.

33. Метод Хаусхолдера

Метод Хаусхолдера позволяет привести матрицу к трехдиа­гональному виду, выполнив почти вдвое меньше вычислений по сравнению с другими методами. Это обусловлено тем, что при его применении становятся нулевыми сразу все элементы строк и столбцов, стоящие вне трех диагоналей матрицы. Метод Хаусхол­дера позволяет получить требуемый результат быстрее, чем метод Гивенса, так как связан с выполнением меньшего числа, хотя и более сложных преобразований. Это его свойство особенно ярко проявляется применительно к большим матрицам.

А_k = Р_kA_k-1Р_k, k=1, 2, ..., п-2,

где Aо == А.

Каждая преобразующая матрица имеет вид

u_k u_k^T

P_k = E - -------------- ,

2K_k²

где

u_i,_k = 0 при i = 1, 2, …, k,

u_i,_k = a_k,_i при i = k+2, …, n,

u_k+1,_k = a_k,k+1  Sk.

Здесь

n 1/2

S_k =  a²_k,i

i=k+1

2K²_k = S²_k  ak, k+1 Sk.

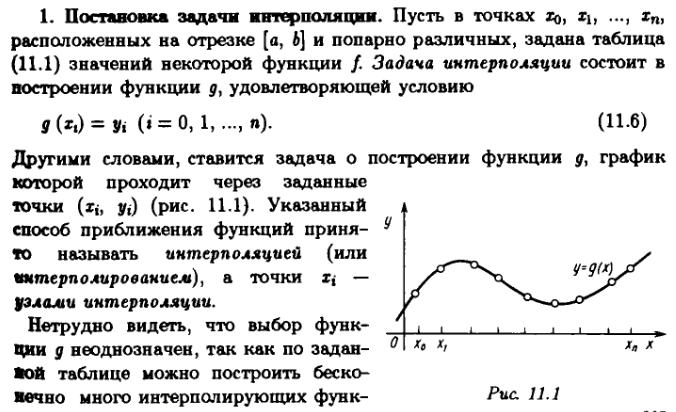
34 Задача и методы интерполяции.Методы Лагранжа и Ньютона

• Интерполяция многочленами

• На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).

• Линейная интерполяция

• Интерполяционная формула Ньютона

• Метод конечных разностей

• Многочлен Лагранжа (интерполяционный многочлен)

• По схеме Эйткена

• Сплайн-функция

Билет 35. Интерполяционный многочлен Лагранжа

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел  , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi.

В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

lj(x) обладают следующими свойствами:

являются многочленами степени n

lj(xj) = 1

lj(xi) = 0 при 

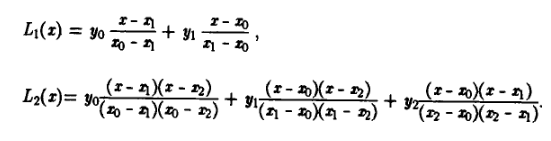
Билет 36.Интерполяционная формула Ньютона.

Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиального интерполирования.

Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то интерполяционный многочлен можно записать в форме Ньютона.

Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).