
Алгоритм распределения ошибки Флойда-Стейнберга
Для порога, равного среднему между минимальной и максимальной интенсивностями, T = (Белый + Черный)/2, алгоритм формулируется следующим образом.
Xmin, Xmax, Ymin, Ymax — пределы растра T = (Черный + Белый)/2 for y = Ymax to Ymin step -1 для каждого пиксела на строке (слева направо) for x = Xmin to Xmax определяем выводимое значение пиксела для пороговой величины T и вычисляем ошибку if I(x, y) < Т then Пиксел(x, y) = Черный Ошибка = I(x, y) - Черный else Пиксел(x, y) = Белый Ошибка = I(x, y) - Белый end if изображаем пиксел Display Пиксел(x, y) распределяем ошибку на соседние пикселы I(x + 1, y) = I(x + 1, y) + 3 * 0шибка/8 I(x, y - 1) = I(x, y - 1) + 3 * Ошибка/8 I(x + 1, y - 1) = I(x + 1, y - 1) + Ошибка/4 next x next y finish
Распределение ошибки на соседние пикселы улучшает вид деталей изображения, так как информация, заключенная в изображении, не теряется.
Существует
другой метод улучшения визуального
разрешения для двухуровневых дисплеев
без уменьшения пространственного
разрешения — метод возбуждения. В
изображение вводится случайная ошибка,
которая добавляется к интенсивности
каждого пиксела до ее сравнения с
выбранной пороговой величиной. Добавление
совершенно произвольной ошибки не
приводит к оптимальному результату.
Тем не менее существует оптимальная
аддитивная матрица ошибки, минимизирующая
эффекты появления фактуры на изображении.
Матрица ошибки добавляется к изображению
таким же способом, как расположены
клетки на шахматной доске. Данный метод
называется упорядоченным возбуждением.
Минимальная матрица упорядоченного
возбуждения имеет размер 2 * 2. Оптимальная
2 * 2-матрица, которую первым предложил
Лим, имеет вид:
![]()
Матрицы
4 * 4, 8 * 8 и больших размеров получают с
помощью рекуррентных соотношений
(n => 4)
![]()
где
n — размер матрицы и

Например,
матрица возбуждения размера 4 * 4 имеет
вид:
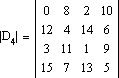
Как показывают два этих примера, из матрицы возбуждения Dn можно породить n2 интенсивностей. С увеличением n изображение не теряет пространственного разрешения. Приведем алгоритм упорядоченного возбуждения.
Алгоритм упорядоченного возбуждения
Xmin, Xmax, Ymin, Ymax — пределы растра Mod — функция, возвращающая остаток от целого деления первого аргумента на второй for y = Ymax to Ymin step -1 для каждого пиксела на строке (слева направо) for x = Xmin to Xmax определяем позицию в матрице возбуждения i = (x Mod n) + 1 j = (y Mod n) + 1 определяем выводимое значение пиксела if I(x, y) < D(i, j) then Пиксел(x, y) = Черный else Пиксел(x, y) = Белый end if изображаем пиксел Display Пиксел(x, y) next x next y finish
На рис17.6c показано изображение, полученное из фотографии на На рис17.6a в результате обработки ее с матрицей упорядоченного возбуждения размера 8 * 8. При использовании матрицы такого размера эффективно вводится 64 уровня интенсивности. На рис17.6c свидетельствует о том, что восстанавливается много мелких деталей. Алгоритм Флойда-Стейнберга и упорядоченное возбуждение можно применять к цветным изображениям. Конфигурационные методы тоже можно использовать с цветом.
Псевдогра́фика, псевдографические символы — совокупность символов, включенных в набор символов компьютерного шрифта, отображающих графические примитивы (линии, прямоугольники, треугольники, кресты, различная заливка и т. п.). Псевдографические символы реализуются в рамках формата (к примеру, матрица 8х12 точек) шрифта и дополняют в таком наборе цифро-буквенные и служебные символы.
Основное назначение псевдографики — графическое оформление программ с текстовым интерфейсом пользователя (в том числе и т. н. консольных) — отображение в них окон, меню, кнопок и прочих элементов интерфейса, создания рамок и таблиц. Первоначальная цель применения — изображение рамок и таблиц на текстовых терминалах. Псевдографика также зачастую используется там, где передача, хранение и визуализация графики непосредственно невозможна или затруднена: телетайпы, текстовые терминалы, почтовая переписка, СМС и т. п.
В системах с графическим интерфейсом псевдографика практически не используется, поскольку там есть возможность отрисовывать те же графические элементы с более высоким качеством и изобразительностью, используя встроенные графические средства системы (скажем, GDI). Кроме того, возможность рисовать рамки псевдографикой ограничена — аккуратно это можно делать только используя шрифты фиксированной ширины.
Другой вид псевдографики используется когда недоступны и псевдографические символы. В этом случае используются доступные и визуально схожие с псевдографикой символы: !, I, O, -, =, +, и т. п. Поэтому псевдографикой можно считать и широко применяющиеся при виртуальном общении составленные из нескольких цифробуквенных символов комбинации — смайлики (впрочем, непосредственное вхождение их в состав некоторых наборов символов (к примеру, Юникод) позволяет им считаться полноценными псевдографическими символами).
Псевдографика также породила отдельный род графического искусства — ASCII-art (аски-арт) — создание рисунков при помощи символов псевдографики.
Гамма-коррекция — коррекция яркости цифрового изображения с помощью степеннóй функции. Гамма-коррекция позволяет:
приспособить изображение под устройство ввода-вывода с нелинейной яркостной характеристикой;
повысить контрастность, разборчивость тёмных участков изображения, не делая при этом чрезмерно контрастными или яркими светлые детали снимка.
Значение γ=1 соответствует «идеальному» монитору, который имеет линейную зависимость отображения от белого к чёрному. Но таких мониторов не бывает — зависимость, в особенности для электронно-лучевых устройств, нелинейна. Большее значение гаммы означает более высокую нелинейность этой зависимости. Стандартное значение гаммы для стандарта видеоизображений NTSC — 2.2. Для дисплеев компьютера значение гаммы обычно составляет значения от 1.5 до 2.0.[1]
