У Т В Е Р Ж Д А Ю
Первый проректор СПГГИ (ТУ)
профессор
____________ Н.В. ПАШКЕВИЧ
" ____ " _______________ 2006 г.
ТЕСТЫ К ЭКЗАМЕНУ
по учебной дисциплине
Теоретическая механика
для студентов специальностей:
1 50402– (Гм) Горные машины и оборудование
1 50404 - (Мм) Металлургические машины и оборудование
Направление:
1 50400 – Технологические машины и оборудование
Вариант II
Составитель: доц. М.Ю. Платовских
Зав. кафедрой: проф. Л.К. Горшков
Декан: проф. А.Г. Протосеня
Санкт-Петербург
2006
№ |
Вопросы |
Варианты ответов |
|
|||
1 |
2 |
3 |
|
|||
|
|
Четвертая аксиома статики в векторном виде записывается так |
|
|
|||
|
|
Тело находится в равновесии под действием только двух сил. Каковы необходимые и достаточные условия для этих сил |
|
|
|||
|
|
F - сила, r - радиус-вектор, d –расстояние от центра О до лини действия силы, h - расстояние от центра О до точки приложения силы. Найти момент силы относительно центра O (как скаляр). |
|
|
|||
|
|
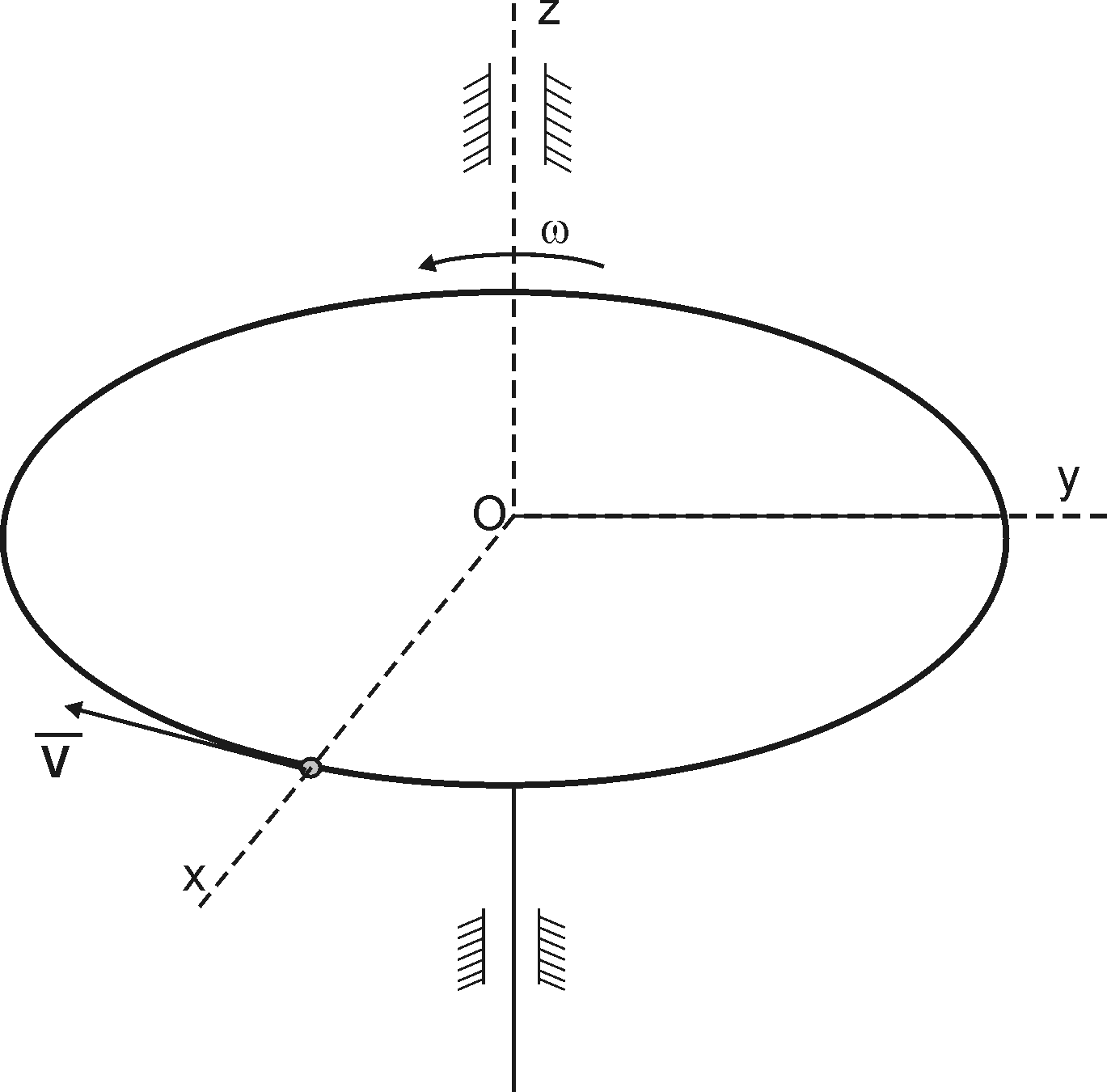
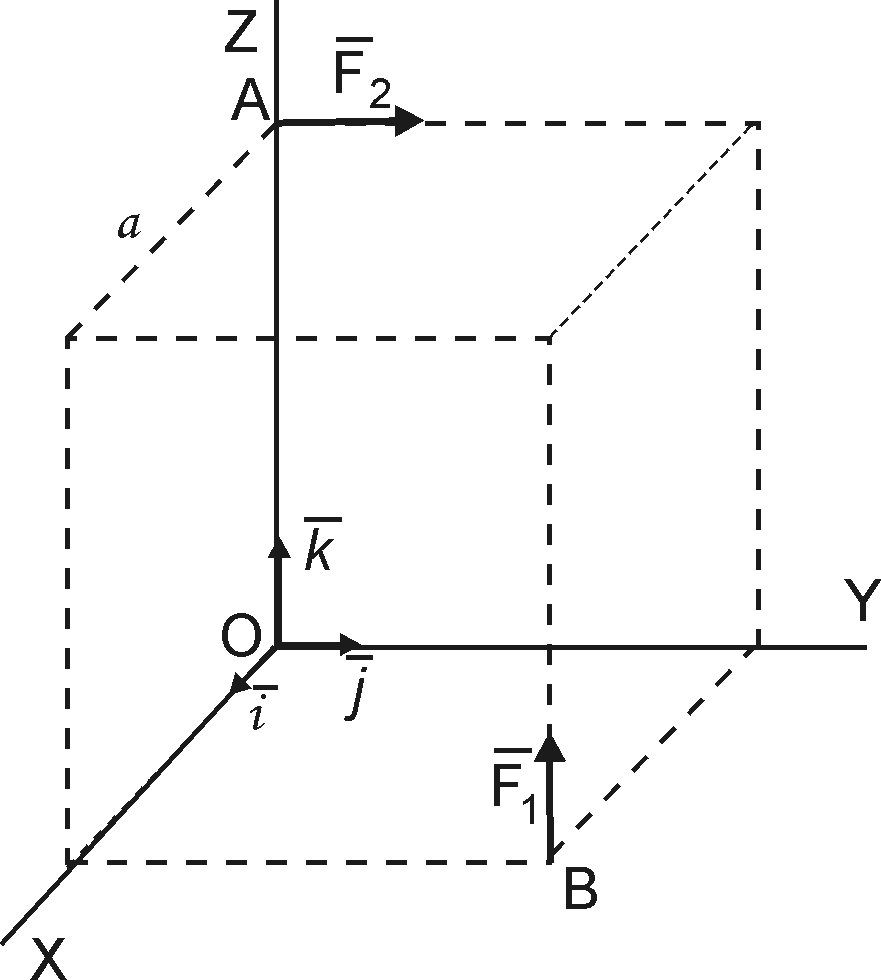
В
|
1. Силе F= 2 H, направленной по оси х’, и паре с моментом М= -8 Нм; 2. Силе F= 2 H, направленной по оси х’, и паре с моментом М= 8 Нм; 3. Силе F= 2 H, направленной по оси х’,и паре с моментом М= 4 Нм; 4. Силе F= 2 H, направленной по оси х’, и паре с моментом М= -4 Нм; 5. Силе F= 2 H, направленной по оси х’. |
|
|||
|
|
Действующая на тело система сил приводится к главному моменту Мо и главному вектору F. При каком условии система приводится к равнодействующей силе?
|
|
|
|||
|
|
Действующая на тело система сил приводится к главному моменту Мо и главному вектору F. При каком условии система приводится к равнодействующей паре?
|
|
|
|||
1 |
2 |
3 |
|
|||
|
|
Найти модуль равнодействующей двух сил, изображенных на рисунке
|
|
|
|||
|
|
В
|
|
|
|||
|
|
Дана уравновешенная система из четырёх сил с модулями 2Н, 3Н, 4Н, 9Н. Чему равен модуль равнодействующей этих сил
|
|
|
|||
|
|
Лемма Пуансо позволяет |
|
|
|||
|
|
Указать вариант с правильными направлениями реакций связей |
1. 2. 3.
4. 5.
|
|
|||
1 |
2 |
3 |
|
|||
|
|
Указать вариант с правильными направлениями реакций связей |
1. 2.
3. 4.
5.
|
|
|||
|
|
Брусок находится на горизонтальной плоскости. На него действует сила, линия действия которой составляет угол с вертикалью. Коэффициент трения покоя f. Найти значение угла , при превышении которого брусок начинает скользить по плоскости.
|
|
|
|||
|
|
Указать вариант с правильными направлениями реакций связей |
1. 2. 3.
4. 5.
|
|
|||
1 |
2 |
3 |
|
|||
|
|
Указать вариант с правильными направлениями реакций связей |
1. 2.
3. 4.
5.
|
|
|||
|
|
С
|
1.
2.
3.
4.
5.
|
|
|||
|
|
Найти
|
1.
2.
3.
4.
5.
|
|
|||
|
|
Найти
|
1.
2.
3.
4.
5.
|
|
|||
1 |
2 |
3 |
|
|||
|
|
Н |
1.
2.
3.
4.
5.
|
|
|||
|
|
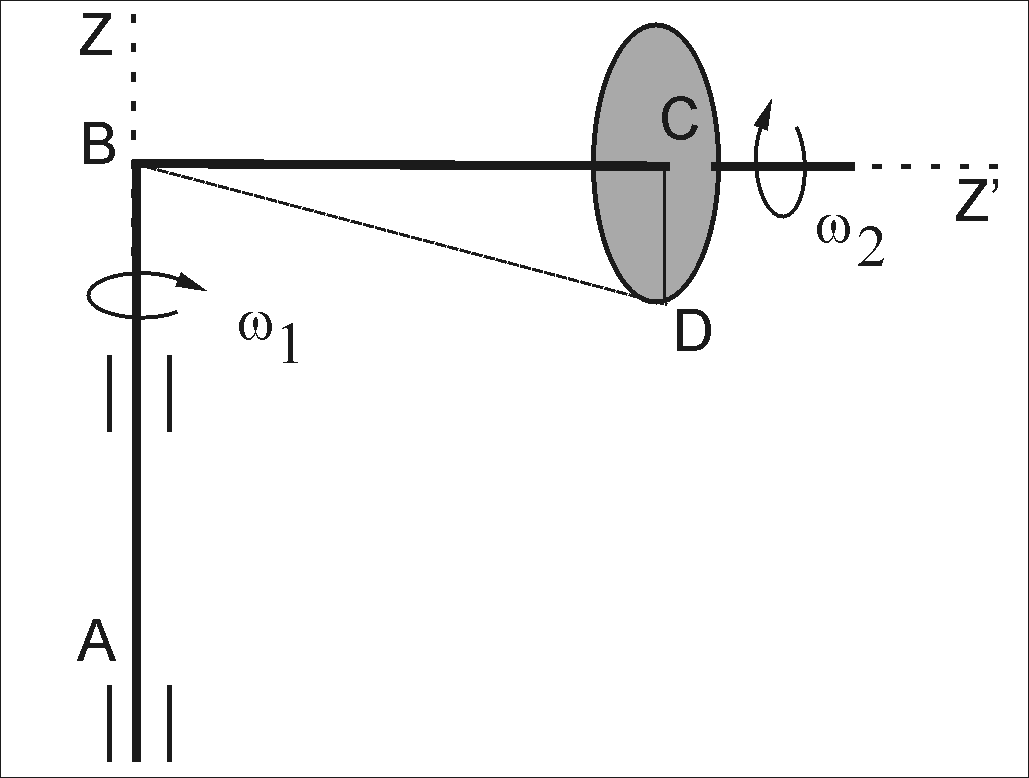
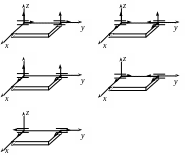
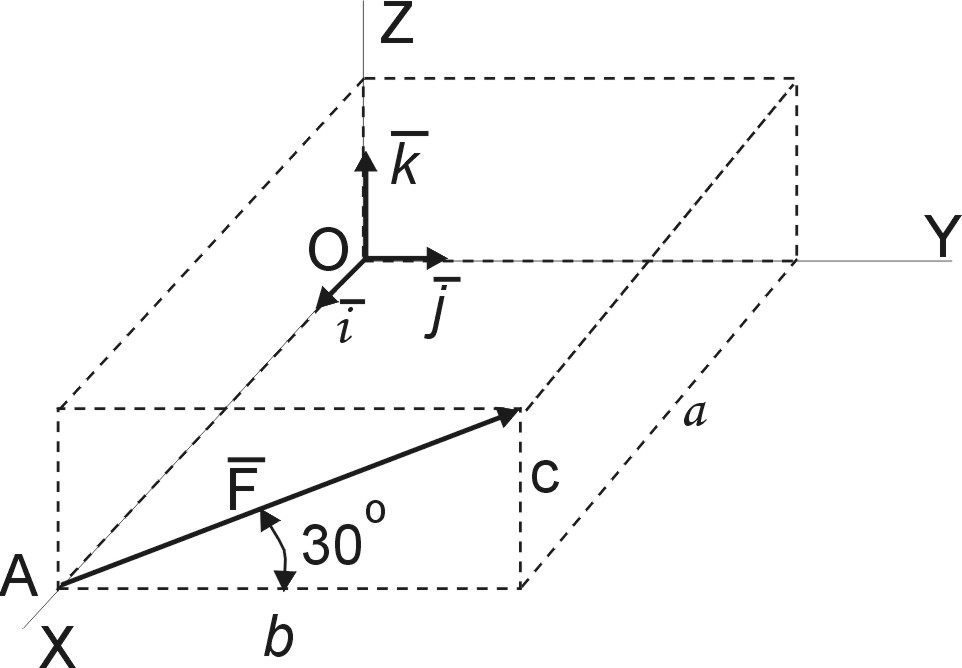
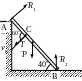
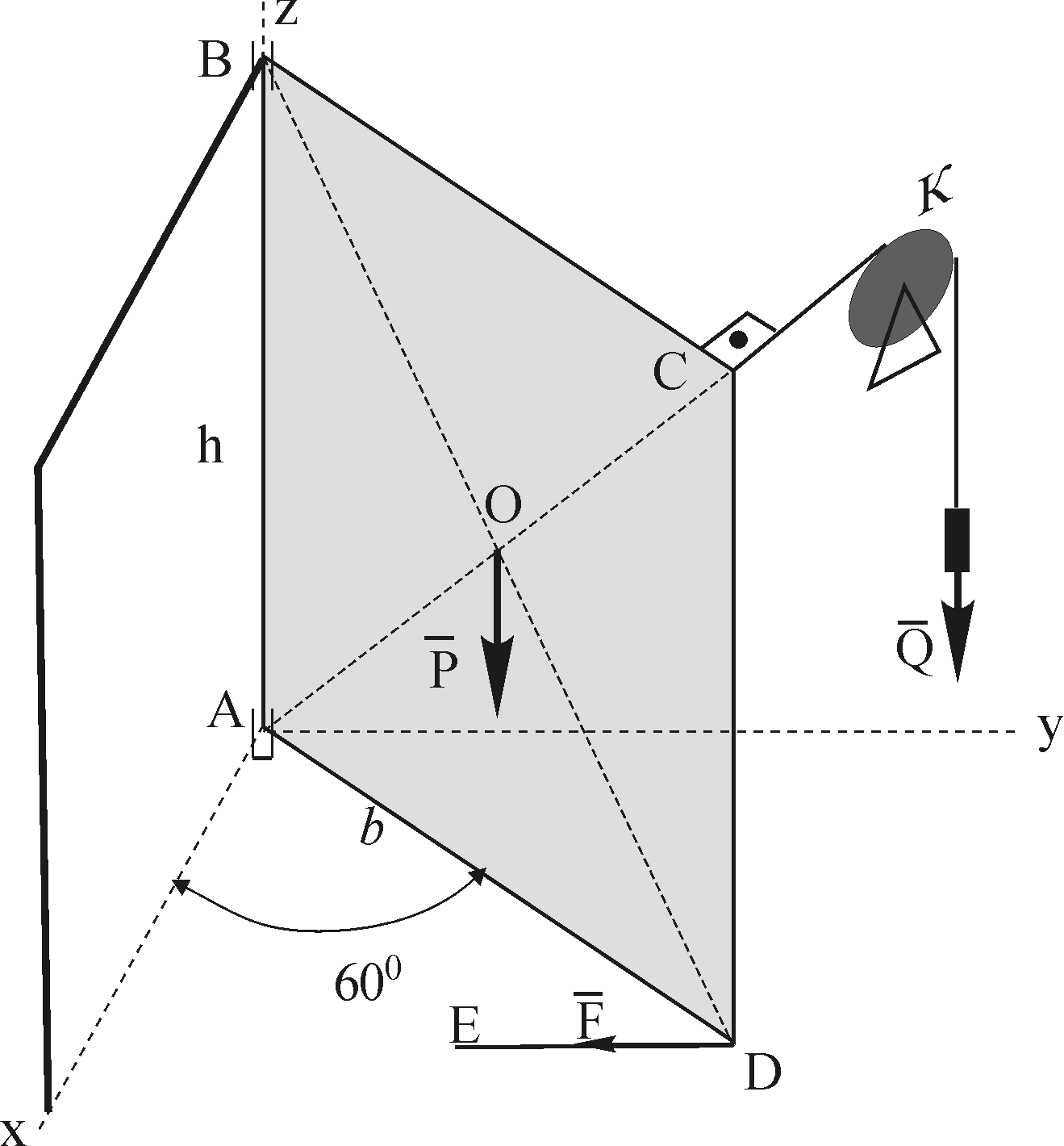
Прямоугольная однородная дверь АВСD веса Р удерживается приоткрытой двумя веревками СК и DE. Найти момент силы натяжения веревки СК относительно оси Аx.
|
1.
2.
3.
4.
5.
|
|
|||
|
|
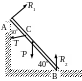
Прямоугольная
однородная полка АВСD
веса Р
удерживается в горизонтальном
положении тросом ЕН и цилиндрическими
шарнирами А и В. Трос ЕН составляет с
полкой угол
и лежит в плоскости, перпендикулярной
оси х.
Найти
|
1.
2.
3.
4.
5.
|
|
|||
1 |
2 |
3 |
|
|||
|
|
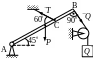
Найти , если АВ – однородная балка весом Р, Q – вес груза.
|
|
|
|||
|
|
Пара сил с плечом d = 0,2 м состоит из сил F иF , причем F = F = 5Н. Направление вращения – против часовой стрелки. Найти эквивалентную пару в той же плоскости |
|
|
|||
|
|
Точка
движется по окружности. При этом
криволинейная координата точки
изменяется по закону
|
|
|
|||
|
|
Точка движется в пространстве по криволинейной траектории из М0 в М1. Определить направление вектора средней скорости на указанном перемещении.
|
|
|
|||
|
|
Т
|
|
|
|||
1 |
2 |
3 |
|
|||
|
|
Радиус-вектор
точки
|
|
|
|||
|
|
Точка
движется в неподвижной системе
координат 0xyz
по закону x
= at,
y
= b,
z
= ct2,
где a,
b,
c
– константы. Найти радиус-вектор
положения
|
|
||||
|
Точка движется по кривой с постоянной по модулю скоростью. Каков угол a между векторами полного и нормального ускорения? |
|
||||
|
|
Движение точки задано в координатной форме x = 5t, y = 15t2+7. Найти модуль ускорения точки. |
|
||||
|
|
Точка движется так, что wt = 0; wn = const ¹ 0. Как и по какой траектории движется точка? |
|
||||
|
|
Радиус-вектор
точки
|
1.
2.
4.
|
||||
|
|
Угол между векторами скорости и ускорения –900. Как движется точка? |
|
||||
|
|
Движение точки задано в координатной форме x = 5t, y= 15t2+7. Найти уравнение траектории |
|
||||
1 |
2 |
3 |
||||
|
|
Материальная
точка движется с постоянной по
направлению, но переменной по модулю
скоростью. Как направлен вектор
ускорения
|
|
||||
|
|
Твердое
тело движется поступательно. Ускорение
точки А этого тела равно
|
|
||||
|
|
Твердое тело вращается вокруг неподвижной оси. Угловое ускорение изменяется по закону = 6at + 2b, где a, b – константы, t – время. Найти закон вращения тела. В начальный момент угол поворота тела равен нулю.
|
|
||||
38. |
Твёрдое тело вращается вокруг неподвижной оси с угловой скоростью и угловым ускорением . Радиус-вектор точки М равен . Найти скорость и ускорение точки М.
|
|
||||
|
|
Твёрдое тело вращается вокруг неподвижной оси с угловой скоростью и угловым ускорением . Найти полное ускорение точки, отстоящей от оси вращения на расстояние h.
|
|
||||
|
|
Как называется движение точки относительно подвижной системы координат, которая, в свою очередь, движется относительно неподвижной системы координат?
|
|
||||
1 |
2 |
3 |
||||
|
|
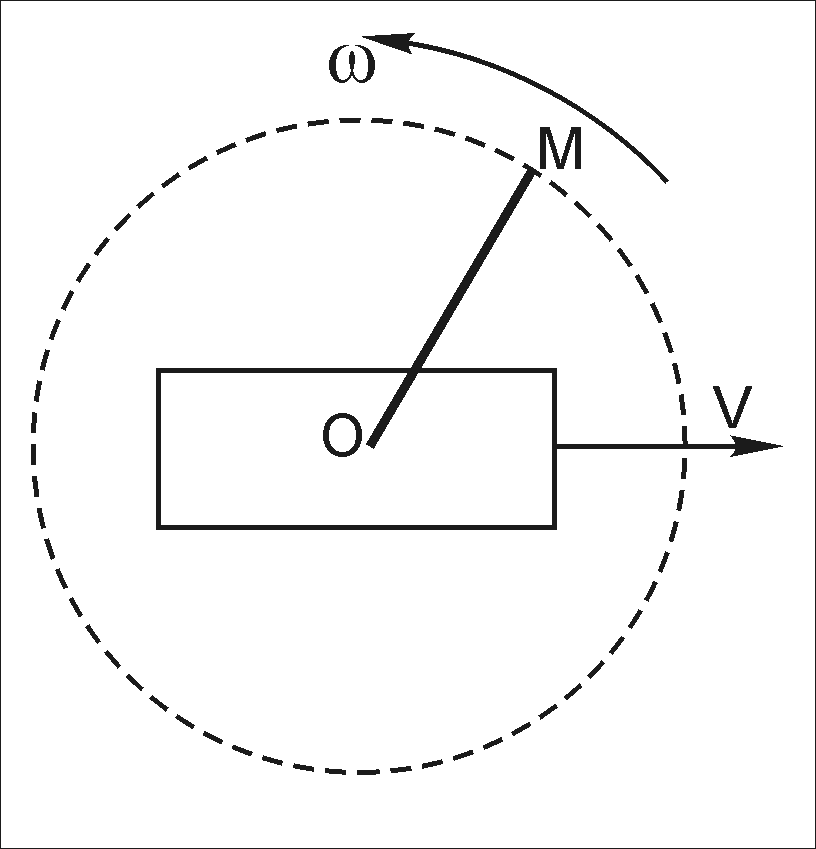
Точка движется по ободу диска, вращающегося против часовой стрелки с угловой скоростью = 10 c-1. Скорость точки относительно диска v=5 м/с. Найти модуль и направление ускорения Кориолиса wc:
|
|
||||
|
|
В условиях предыдущей задачи найти модуль и направление абсолютной скорости точки, если радиус диска равен 1м. |
|
||||
|
|
А
|
|
||||
1 |
2 |
3 |
||||
|
|
О
|
|
||||
|
|
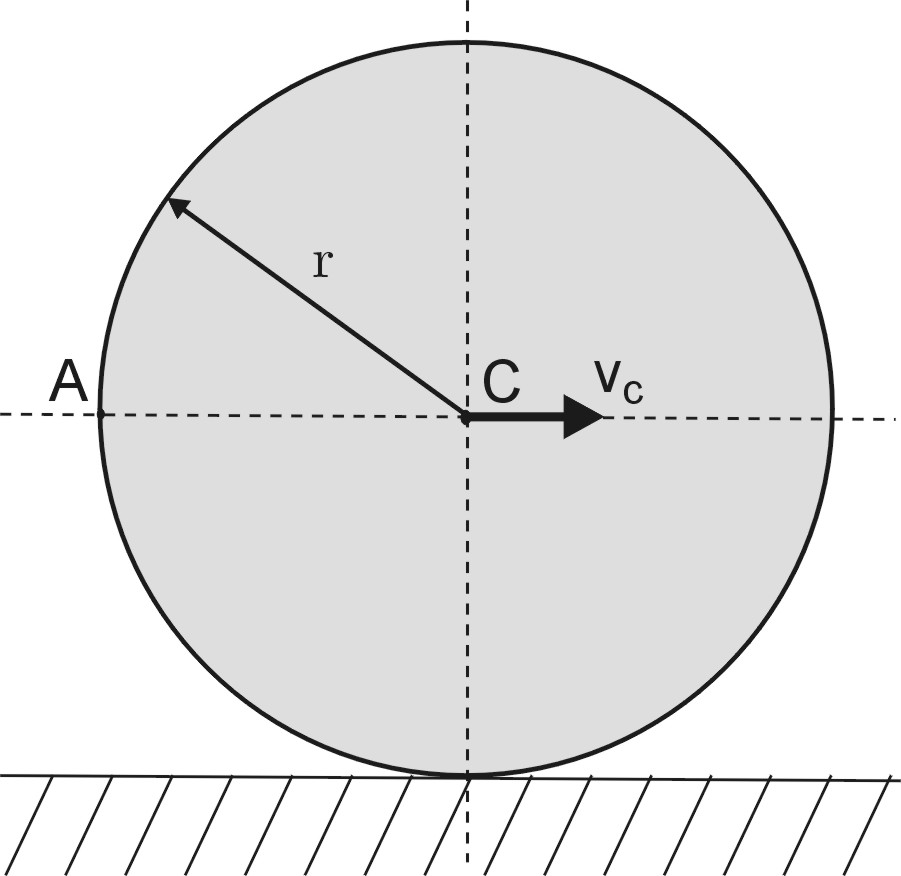
Отрезок
АВ совершает плоское движение.
|
|
||||
|
|
Д
|
|
||||
|
|
-
скорость полюса А,
- угловая скорость фигуры. Найти
скорость точки В плоской фигуры,
|
|
||||
|
|
Отрезок
АВ совершает плоское движение.
|
|
||||
1 |
2 |
3 |
||||
|
|
Плоское движение тела задано уравнениями xA = f1(t), yA = f2(t), j = j(t), где xA, yA – координаты полюса А, j - угол поворота вокруг А. Изменятся ли уравнения движения, если за полюс взять точку В?
|
|
||||
|
|
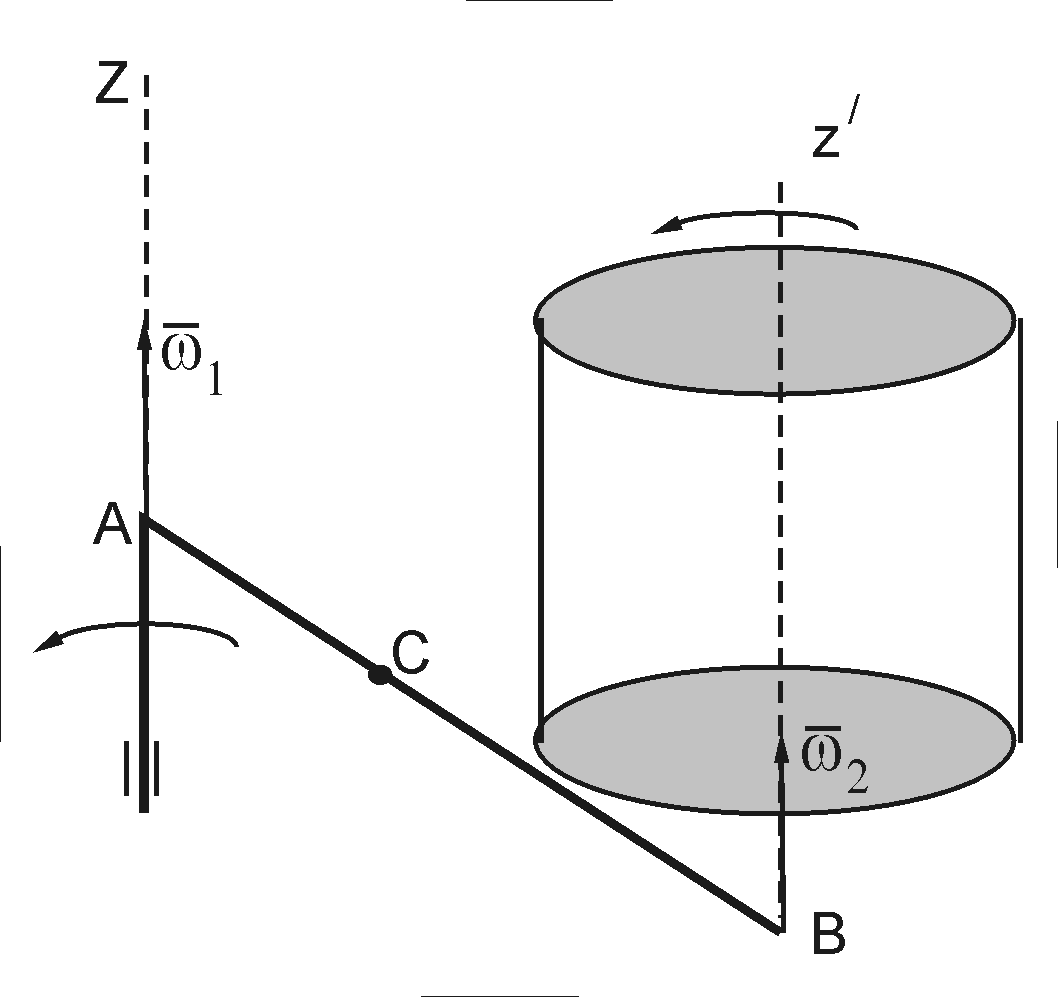
Ц
Чему равна абсолютная угловая скорость и как расположена мгновенная ось вращения, вдоль которой она направлена?
|
|
||||
|
|
П
|
|
||||
1 |
2 |
3 |
||||
|
|
Где находится мгновенный центр скоростей плоской фигуры, если в данный момент времени угловая скорость её вращения равна нулю? |
|
||||
|
|
Закон инерции (I – ый закон динамики) |
|
||||
|
|
Тело, имевшее начальную скорость 2 м/с через 10 с после начала движения остановилось. Пройденный при этом путь равен |
|
||||
|
|
Мерой инерции материальных тел служит |
|
||||
|
|
Какое равенство не является одной из форм записи или следствием основного закона динамики |
|
||||
|
|
Первая, или прямая, задача динамики точки сводится |
|
||||
1 |
2 |
3 |
||||
|
|
Груз, подвешенный на пружине, совершает свободные колебания. Затем этот же груз подвесили на пружину вчетверо большей жесткости. Как при этом изменилась частота свободных колебаний? |
4. Увеличилась в два раза 5. Уменьшилась в три раза
|
||||
|
|
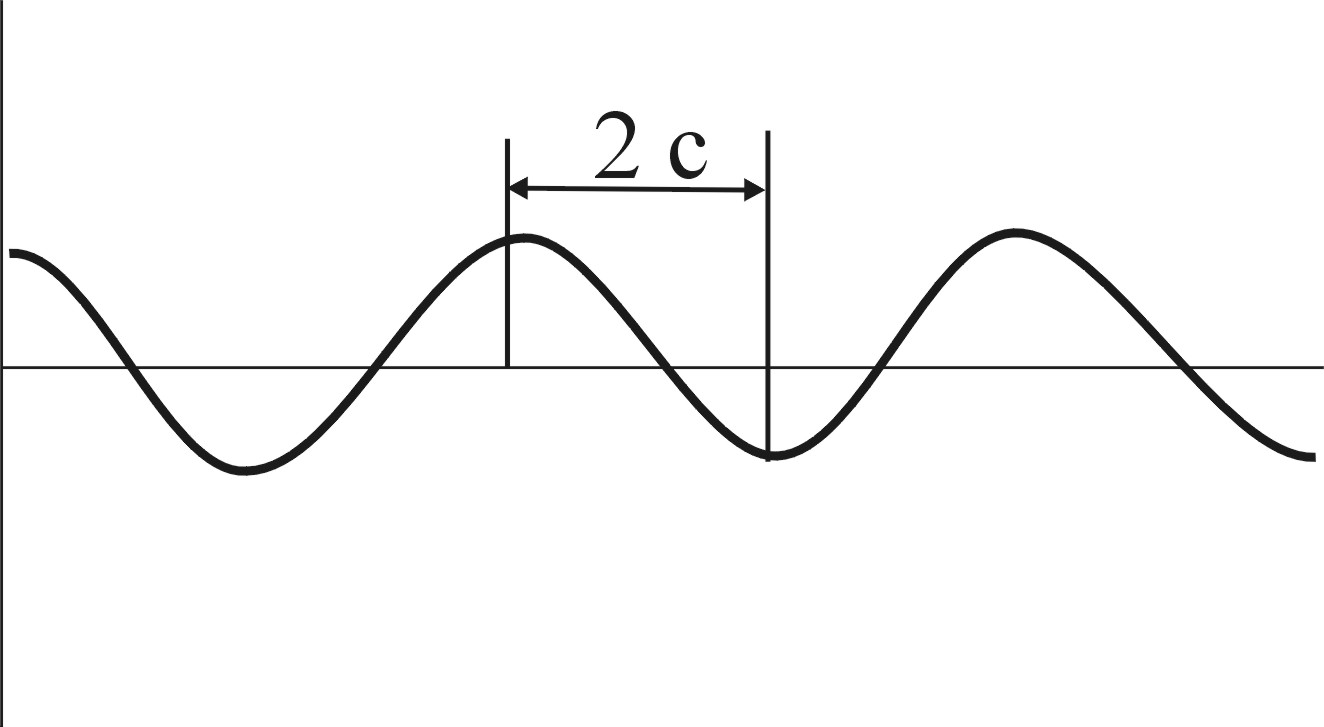
Груз
массой 10 кг, подвешенный на пружине,
совершает свободные колебания. Два
его последовательные наибольшие
отклонения от положения статического
равновесия разделяет отрезок времени
2 с. Найти жесткость пружи
|
|
||||
|
|
Укажите
верное выражение для резонансной
амплитуды вынужденных колебаний
(р=k)
при действии сил сопротивления ( EMBED
Equation.DSMT4
|
|
||||
|
|
Груз совершает вынужденные колебания в среде с сопротивлением. Как изменится значение его резонансной амплитуды Арез, если при прочих равных условиях его массу заменили на вчетверо большую.
|
|
||||
|
|
Сила F, действующая на материальную точку массы 5 кг, равная нулю при t=0 и линейно увеличиваясь со временем, достигает 100 Н через 10 с.На какую величину изменилась за это время скорость точки. |
|
||||
1 |
2 |
3 |
||||
|
|
Тело массой 10 кг, имевшее начальную скорость 20 м/с при движении по прямолинейной траектории под действием силы сопротивления остановилось через время 20 с. Определить величину силы сопротивления F.
|
|
||||
|
|
Укажите верную формулировку теоремы о кинетическом моменте точки относительно центра |
|
||||
|
|
Укажите векторную формулу для кинетического момента точки относительно центра |
|
||||
|
|
Теорема о кинетическом моменте точки относительно оси Z характеризуется равенством |
|
||||
|
|
Равенством, выражающим связь между кинетическим моментом точки относительно оси и центра, лежащего на этой оси, является |
|
||||
|
|
Элементарная
работа EMBED Equation.3
|
|
||||
1 |
2 |
3 |
||||
|
|
Аналитическая формула элементарной работы EMBED Equation.3 имеет вид |
|
||||
|
|
К
|
|
||||
|
|
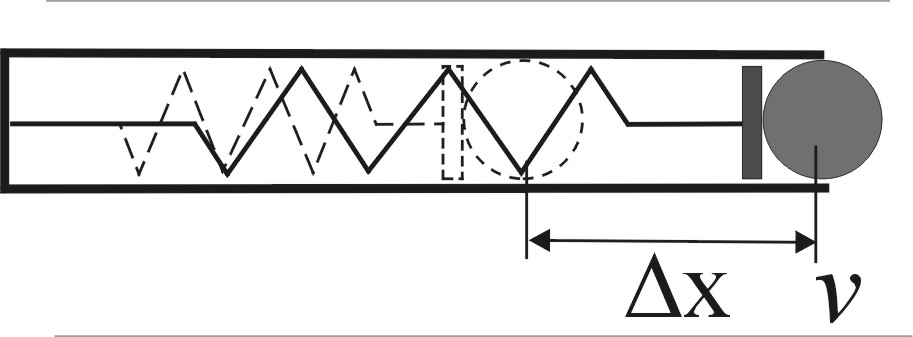
Для
зарядки шарикового пистолета его
пружину жесткостью с
с шариком массой m
на конце сжали от недеформированного
состояния (совпадает с концом «ствола»)
на величину х.
На какое EMBED Equation.3
|
|
||||
|
|
Мощность силы определяется равенством |
|
||||
|
|
Груз веса P падает с высоты Н на пружину жесткостью с, находящуюся изначально в недеформированном состоянии. Насколько будет сжата пружина? |
|
||||
1 |
2 |
3 |
||||
|
|
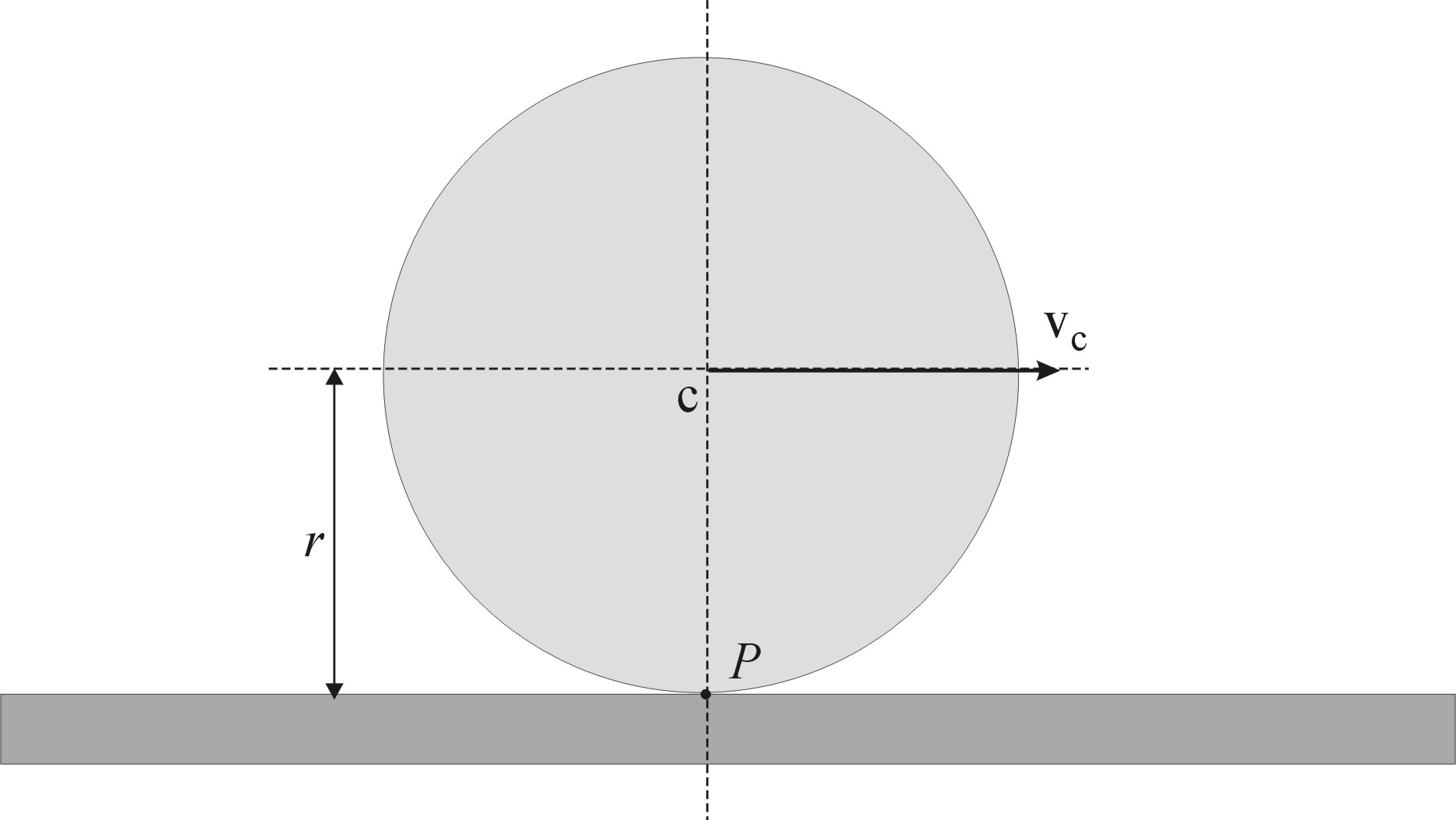
Санки массой m скатываются без начальной скорости с горы, имеющей профиль ¼ окружности. Трение не учитывается. С какой по модулю силой санки давят на снег в нижней точке горы? |
|
||||
|
|
Основное
уравнение метода кинетостатики для
материальной точки массы m
имеет вид ( EMBED Equation.3
|
1.
EMBED Equation.3
2.
EMBED Equation.3
3.
EMBED Equation.3
4.
EMBED Equation.3
5.
EMBED Equation.3
|
||||
|
|
Автомобиль массы m и двигателем мощностью N начал двигаться из состояния покоя по криволинейной траектории. Пройдя путь S за время t автомобиль остановился. Чему равна работа сил, приложенных к автомобилю на этом перемещении.
|
|
||||
|
|
Чему равна сила инерции точки |
|
||||
|
|
Потенциальная энергия некоторого поля выражается равенством EMBED
Equation.3
Проекции силы поля на оси координат имеют вид
|
|
||||
|
|
Центр масс механической системы определяется формулой |
|
||||
1 |
2 |
3 |
||||
|
|
Укажите верную формулировку теоремы о движении центра масс |
|
||||
|
|
Количество движения системы равно |
1. EMBED Equation.3 2.
EMBED
Equation.3
3. EMBED Equation.3 4.
EMBED
Equation.3
5.
EMBED
Equation.3
|
||||
|
|
Кинетический момент системы относительно центра равен |
|
||||
|
Кинетический
момент твердого тела относительно
оси вращения EMBED Equation.3
|
|
||||
|
|
Теорема о кинетическом моменте системы относительно оси z имеет вид |
|
||||
|
|
Центробежный
момент инерции твёрдого тела EMBED
Equation.3
|
|
||||
1 |
2 |
3 |
||||
|
|
Укажите правильную формулу для радиуса инерции тела относительно оси EMBED Equation.3 |
1.
EMBED Equation.3
3.
EMBED Equation.3
|
||||
|
|
Момент инерции однородного стержня относительно оси, проходящей через край стержня перпендикулярно его оси, равен |
|
||||
|
|
Чему равен момент инерции сплошного однородного диска массой m и радиуса r относительно оси перпендикулярной плоскости диска и проходящей через точку на краю
|
|
||||
|
|
Дифференциальное уравнение вращения твёрдого тела относительно неподвижной оси EMBED Equation.3 имеет вид |
|
||||
|
|
Какой формулой определяется кинетическая энергия плоско-параллельного движения |
|
||||
|
|
Теорема о кинетической энергии механической системы в дифференциальной форме имеет вид |
|
||||
1 |
2 |
3 |
||||
|
|
К
|
|
||||
|
|
Принцип возможных перемещений отражает уравнение |
5.
|
||||
|
|
Идеальные связи в механической системе определяются равенством |
|
||||
|
|
Обобщённая
сила
|
1.
3.
|
||||
|
|
Чему равен кинетический потенциал системы L |
5. Т2 + П2 |
||||
|
|
В положении устойчивого равновесия потенциальная энергия |
|
||||
1 |
2 |
3 |
||||
|
|
Обобщённая сила для материальной системы в потенциальном силовом поле равна |
1.
;
2.
3.
;
4.
|
||||
|
|
Уравнение Лагранжа второго рода для системы с одной обобщённой координатой имеет вид |
|
||||
|
|
Уравнение Лагранжа второго рода для системы в потенциальном силовом поле имеет вид |
|
||||
Составитель:
доцент М.Ю. Платовских
Эксперты:
доцент В.Н. Монахов
профессор М.М. Ветюков
Заведующий кафедрой механики,
профессор Л.К. Горшков





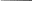








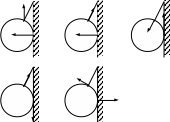
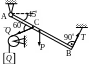







 айти
айти
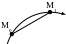
 очка
движется по криволинейной траектории.
0 – начало координат, М0
– начальное положение, М1,
М2
– последовательные положения точки
в моменты времени t1
и t2.
Найти путь, пройденный точкой к моменту
времени t2.
очка
движется по криволинейной траектории.
0 – начало координат, М0
– начальное положение, М1,
М2
– последовательные положения точки
в моменты времени t1
и t2.
Найти путь, пройденный точкой к моменту
времени t2.