5. Задания

1. Для заданного целого n ≥ 0 вычислить:

а) ( 2n + 1 )!! = 1·3·5·...· ( 2k + 1 ) ;

б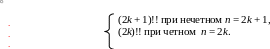 ) ( 2n )!! = 1·2·4·6·...· ( 2n ) ;

n!!=

в) n!!, где

2. Для заданного целого n ≥ 0 вычислить S(n) = S _i = 0…n a(i); вид слагаемых a(i) определяется вариантами:

а) a(i) = i! ;

б) a(i) = i!·i; для “контроля” учесть, что S(n) = (n + 1)! – 1 ;

в) a(i) = kⁱ , где k > 0 – заданное целое ;

г) a(i) = (n – i) kⁱ, где k > 1 – заданное целое ;

д) a(i) = A(n – i | m) , где m – заданное целое (m ≥ n);

е) a(i) = A(n | m + i) , где m – заданное целое (m ≥ n);

для вариантов д) и е) A(t | r) = r!/(r – t)! = r (r – 1) ... (r – t + 1).

3. Для целых p ≥ q ≥ 0 определим (p | q) = p!/(q! (p – q)!).

Для заданного целого n ≥ 0 вычислить:

а) S(n) = S_{i = 0...([n / 2])} a(i) , где a(i) = (n | 2i), для “контроля” учесть, что S(n) = 2^n – 1;

б) S(n) = S_{i = 0...([ n / 2])} a(i), где a(i) = (n | 2i + 1), для “контроля” учесть, что S(n) = 2^n – 1;

в) S(n) = S_i = 0...n a(i), где a(i) = (n | i), для “контроля” учесть, что S(n) = 2ⁿ ;

г) S(n) = S_i = 1...n a(i), где a(i) = i · (n | i); здесь n > 1; для “контроля” учесть, что S(n) = n 2^n – 1;

д) S(n) = S_i = 0...n a(i), где a(i) = (m + i | m), где m — заданное целое (m > 0 ); для “контроля” учесть, что S(n) = (m + n + 1 | m + 1) ;

е) S(n) = S_i = 0...n a(i), где a(i) = (m | i) (–1)ⁱ , где m — заданное целое (m > n); для “контроля” учесть, что S(n) = (m – 1 | n) · (–1)ⁿ.

4. Задана последовательность чисел Фибоначчи {F(n)}.

А) Для заданного целого n ≥ 0 вычислить:

а) F(n);

б) S(n) = S_i = 0...n a(i), где a(i) = F(i); для “контроля” учесть, что S(n) = F(n + 2) – 1 ;

в) Ф(n) — элемент последовательности Фибоначчи второго порядка, определяемой условиями Ф(0) = 0, Ф(1) = 1, Ф(n + 2) = Ф(n + 1) + Ф(n) + F(n); для “контроля” полезно знать, что Ф(n) =  ((3n + 3)/5) F(n) – (n/5) F(n + 1).

Б) Для заданного целого m > 1 найти:

а) первое по порядку число Фибоначчи F(n), большее m ;

б) первое по порядку число Фибоначчи второго порядка Ф(n), большее m (см. п. 4.А.в) ;

в) наименьшее n, такое, что S(n) > m, для S(n) определенного в п. 4.А.б.

5. Пусть задано m > 0 целое. Последовательность {A(n)} определяется условиями A(0) = 0, A(1) = 1, A(n + 2) = A(n + 1) + A(n) + (n | m), где (n | m) определено в п.3 при n ≥ m ≥ 0, а при n < m положим (n | m) = 0. Тpебуется:

а) для заданного целого n ≥ 0 вычислить A(n) ;

б) для заданного целого k > 1 вычислить первое по порядку А(n), большее k.

6. Целое число k задано в десятичной системе записи. Пользуясь стандаpтными операциями с целыми числами, вычислить следующие хаpактеpистики двоичной записи числа k :

а) N(k) – количество двоичных цифp;

б) N0(k) – количество позиций с цифpой 0;

в) N1(k) – количество позиций с цифpой 1;

г) номеp позиции пеpвой слева (спpава) цифpы 0 (1) – NL0 (k) (NR1(k));

д) номеp позиции i-й слева (спpава) цифpы 0 (1) – NL_i0(k) (NR_i1(k));

е) Nq01(k) – количество позиций с цифpами 0 или 1 в q-ичной (!)

записи числа k.