13

2. СХЕМА ИТЕРАЦИИ И РЕКУРРЕНТНЫЕ ВЫЧИСЛЕНИЯ С ЦЕЛЫМИ ЧИСЛАМИ

1. Общая схема итерации и рекуррентные вычисления

Многие вычисления укладываются в следующую схему:

x

(2. 1)

:=x0;

while B(x) do x:=f(x);

где x – множество переменных программы, x0 – их начальные значения, B(x) – булевская функция (предикат) от переменных x, а f – функция. В соответствии с семантикой цикла while–do предикат B(x) – условие продолжения цикла.

Схему (2.1) иногда называют схемой итерации (от латинского iteratio –повторение), а отдельные шаги цикла — итерациями.

Выбирая различные x, B и f, получим из схемы (2. 1) различные конкретные программы.

Например, полагая

x=<u,v>, x0=<a,b>, , ,

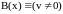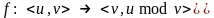получим известный алгоритм Евклида вычисления наибольшего общего делителя (НОД) чисел a и b:

var a, b, u, v, r: Integer;

…

{(a>0) & (b>0)}

u:=a; v:=b;

while v¹0 do

begin

r:=u mod v;

u:=v;

v:=r

end {u=НОД(a,b)}

Все конкретные программы, порождаемые схемой (2.1), обладают некоторыми общими свойствами.

Действительно, пусть цикл while-do в (2.1) завершился за n шагов и переменные x принимали последовательно значения x₀, x₁, …, x_n – 1, x_n, тогда последовательность x_i (i Î [0; n]) обладает свойствами:

1. x_i = f(x_i – 1) для всех i Î [1; n];

2. x

   (2. 2)

   _i ≠ x_j при i ≠ j и i, j Î [0; n];

3. B(x_i) для всех i Î [0; n – 1];

4. not B(x_n).

Свойство 1 следует из семантики оператора присваивания x:=f(x). Свойство 2 выражает необходимое условие завершения цикла. Свойства 3 и 4 следуют из семантики конструкции цикла while-do. Итерации заканчиваются, если существует n, соответствующее свойству 4. При этом значение n является наименьшим из всех таких значений, что определяется свойством 3.

Иногда свойства (2.2) схемы (2.1) рассматривают как “Теорему о линейном просмотре” [23, с.146], поскольку такая программа осуществляет поиск среди значений x₀, x_i = f(x_i – 1), i > 0 значения x_i с минимальным индексом i ≥ 0, при котором истинно not B(x_i).

Очевидно, что схема (2.1) является слишком общей и в таком виде малоинтересна. Любой цикл while-do можно рассматривать как реализацию схемы (2.1). Интерес представляют, как правило, частные случаи этой схемы. Однако и в таком виде она является подходящей формой программ, основанных на рекуррентных соотношениях свойства 1 из (2.2).

2. Вычисления с целыми числами

Рассмотрим двоичное представление натурального числа x:

x = b_m2^m + b_m – 12^m – 1 + … + b₁2¹ + b₀ ,

где b_i Î {0, 1} " i Î[0; m – 1], и b_m = 1, если не записывать незначащие левые нули. Двоичной записью числа x в этом случае является последовательность

< b_m , b_m – 1 , …, b₁ , b₀ >₂ ,

где число двоичных разрядов (бит), необходимых для записи числа x, равно m + 1 = [log₂ x] + 1.

Например:

а) x = 11 = <1011>₂= 1×2³+ 0×2² +1×2¹+ 1×2⁰, число двоичных разрядов m + 1 = [log₂11] + 1 = 3 + 1 = 4;

б) x = 16 = <10000>₂= 1×2⁴+ 0×2³ + 0×2² +0×2¹+ 0×2⁰, число двоичных разрядов m + 1 = [log₂16] + 1 = 4 + 1 = 5;

в) x = 15 = <1111>₂ = 1×2³+ 1×2² +1×2¹+ 1×2⁰, число двоичных разрядов m + 1 = [log₂15] + 1 = 3 + 1 = 4.

Для хранения натурального числа в памяти ЭВМ отводится фиксированное количество бит. При этом двоичная запись числа выравнивается в отведенной ячейке памяти по правому краю (младшие биты числа и ячейки совпадают), а “свободные” биты ячейки слева заполняются нулями. Например, для типа Byte в Турбо Паскале под запись целого числа без знака отводится 8 бит, т. е. 1 байт. Число x = 11 представляется здесь как <00001011>₂. Максимальное по значению число типа Byte есть <11111111>₂ = 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 2⁸ – 1 = 255.

Отрицательные целые числа представляются специальным образом, например в так называемом дополнительном коде [12] (в этом случае число 0 имеет единственное и естественное представление <00...00>₂). При этом выделяется специальный знаковый бит (крайний слева), который для положительных чисел равен 0, а для отрицательных – 1. Например, число стандартного типа Integer в реализации Турбо Паскаля занимает 2 байта, т. е. 16 бит, из которых самый левый бит используется как знаковый. Предопределенная константа, соответствующая максимальному положитель-ному числу типа Integer, MaxInt = 2¹⁵ – 1 = 32767. Диапазон значений типа Integer приведен в табл. 2. 1 (асимметрия границ диапазона вызвана особенностями представления чисел в дополнительном коде). В этой же таблице приведены данные о всех стандартных типах Турбо Паскаля, реализующих представление целых чисел.

Таблица 2.1

Целые типы в Турбо Паскале
Название типа	Диапазон значений	Длина
Shortint Integer Longint Byte Word	–128...127 –32768...32767 –2147483648...2147483647 0...255 0...65535	1 байт ( 8 бит со знаком) 2 байта (16 бит со знаком) 4 байта (32 бита со знаком) 1 байт ( 8 бит без знака) 2 байта (16 бит без знака)

Для работы с целыми числами используются стандартные операции +, –, *, div, mod и функции Abs, Sqr, Odd и некоторые др.

Необходимо учитывать следующие особенности вычислений с целыми числами: 1) вычисления выполняются точно; 2) результаты некоторых операций или функций могут выходить за границы диапазона возможных значений (эффект “переполнения”).

В качестве примера приведём простейшую программу:

var a, b: Integer;

const MinInt=-32768;

begin

a:=MaxInt; b:=MinInt;

Write('a=',a); WriteLn(' b=',b);

a:=a+1; b:=b-1;

Write('a=',a); WriteLn(' b=',b);

end.

Результаты выполнения этой программы приведены в табл. 2. 2.

Таблица 2. 2

Реакция на переполнение (выход за границы диапазона) в Турбо Паскале
Турбо Паскаль 6.0 (опция Overflow checking отсутствует)	Турбо Паскаль 7.0 (опция Overflow checking включена)	Турбо Паскаль 7.0 (опция Overflow checking отключена)
a = 32767 b = –32768 a = –32768 b = 32767	a = 32767 b = –32768 Runtime error 215 (Arithmetic overflow)	a = 32767 b = –32768 a = –32768 b = 32767

В версии Турбо Паскаль 7.0 существует режим контроля переполнения (среди опций компилятора Options/Compiler есть опция Overflow checking). При включенной опции Overflow checking при выполнении оператора a:=a+1 выдается сообщение об ошибке (см. второй столбец табл. 2. 2) и работа программы прекращается. При выключенной опции Overflow checking сообщение об ошибке не выдается (см. третий столбец табл. 2. 2) и результат операции ошибочен (объясните этот результат). В версии Турбо Паскаль 6.0 нет режима контроля переполнения (см. первый столбец табл. 2. 2).

Эти особенности вычислений с целыми числами необходимо учитывать при выполнении заданий (см. далее примеры в 2. 4). Иногда, реорганизовав вычисления (в том числе используя рекуррентный способ вычислений), можно избежать эффекта переполнения в промежуточных результатах.