10. Неопределённый интеграл.

10.1. Первообразная функция.

Опр.10.1. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е. .

Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x) требуется найти функцию F(x), производная которой равна f(x).

Первообразная определена неоднозначно: для функции первообразными будут и функция arctg x, и функция arctg x-10: . Для того, чтобы описать все множество первообразных функции f(x), рассмотрим

Свойства первообразной.

1. Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во: ).

2. Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F₁(x) может быть представлена в виде F₁(x) = F(x) + C, где C - постоянная на X функция.

Док-во. Так как функции F(x) и F₁(x) - первообразные для f(x), то (по теор.8.1. условие постоянства дифференцируемой функции на интервале) .

3. Для любой первообразной F(x) выполняется равенство dF(x) = f(x) dx.

Из этих свойств следует, что если F(x) - некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная.

10.2. Неопределённый интеграл и его свойства.

Опр.10.2. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .

Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то

, где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

Свойства неопределённого интеграла, непосредственно следующие из определения:

1. .

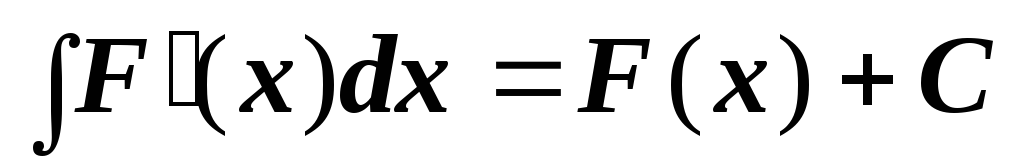2. (или ).

10.3. Таблица неопределённых интегралов.

1	.	11	.
2	.	12	.
3	().	13	.
4	.	14	.
5	;.	15	.
6	.	16
7	.	17	.
8	.	18	.
9	.	19	.
10	.	20	;.

В формулах 14, 15, 16, 19 предполагается, что a>0. Каждая из формул таблицы справедлива на любом интервале, на котором непрерывна подынтегральная функция. Все эти формулы можно доказать дифференцированием правой части. Докажем, например, формулу 4:

если x > 0, то ; если x < 0, то .

Дальше мы докажем, что любая непрерывная функция имеет первообразную и, как следствие, неопределённый интеграл. При изучении дифференцирования было установлено, что с помощью таблицы производных и правил дифференцирования без труда можно получить производную любой элементарной функции, и эта производная тоже будет элементарной функцией. Операция интегрирования этим свойством не обладает: даже относительно простые функции могут иметь первообразные, которые через элементарные функции не выражаются. Так, доказано, что не берутся в элементарных функциях следующие интегралы, относящиеся к классу специальных функций:

- интеграл Пуассона; , - интегралы Френеля; , , - интегральные синус, косинус, логарифм.