28

1. Материа́льная то́чка — простейшая физическая модель в механике — абстрактное тело нулевых размеров. Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого в конкретной ситуации можно пренебречь. Абсолю́тно твёрдое те́ло в механике — механическая система, обладающая только поступательными и вращательными степенями свободы. «Твёрдость» означает, что тело не может быть деформировано, то есть телу нельзя передать никакой другой энергии, кроме кинетической энергии поступательного или вращательного движения. Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей. В зависимости от задач, к этим полям могут добавляться поля других физических величин (концентрация, температура, поляризованность и др.) Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой. Сплошная среда — часто и успешно используемая в физике сплошных сред модель для более-менее однородных систем с очень большим числом частиц (т. е. степеней свободы). Так, теория упругости, гидро- и аэродинамика, физика плазмы формулируются именно для сплошной среды. Однако с точки зрения математической строгости следует помнить об одной неточности: все реальные системы обладают пусть большим, но конечным числом степеней свободы. Сплошная же среда обладает не просто бесконечным, а несчётным числом степеней свободы.

Пространство и время. Все тела сущест-ую и движутся в пространстве и времени. Любое тело имеет объем, т.е. пространственную протяженность. Время выражает порядок смены состояний, составляющих любой процесс, любое движение. Оно служит мерой длительности процесса. Но для изучения движения и других явлений важны не определения, а их св-ва. Время – однородно (мы не в состоянии не ускорить его, не затормозить); одномерно (для указания момента наступления какого-либо события вполне достаточно одного числа); однонаправлено (необратимо). Пространство также однородно (физ-кие законы для любых двух точек пространства одинаковы), изотропно (все физ-кие явления протекают одинаково) и трехмерно (для указания места достаточно трех пространственных координат). Некоторые величины полностью хар-зуются числом, такие величины наз-ся скалярными. Для хар-ки других физ. величин (скорость, сила) недостаточно числа, измерения их величины, но необходимы еще и направления.

Элементы векторной алгебры.Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.Длиной (модулем) вектора называется расстояние между началом и концом вектора.

2. Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени.

     Пусть материальная точка движется по криволинейной траектории и в момент времени t ей соответствует радиус-вектор . (рис. 1.3). В течение малого интервала времени  точка пройдет путь и получит бесконечно малое перемещение . Различают среднюю и мгновенную скорости.      Вектором средней скорости называется отношение приращения радиуса-вектора точки к промежутку времени :

     (1.3)

     Вектор   направлен так же, как  . При неограниченном уменьшении  , средняя скорость стремится к предельному значению, которое называется мгновенной скоростью или просто скоростью:  

      (1.4)

         Таким образом, скорость – это векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости направлен по касательной к траектории в сторону движения.      По мере уменьшения длина дуги все более приближается к длине стягивающей ее хорды, т.е. численное значение скорости материальной точки равно первой производной длины ее пути по времени:

     Таким образом,

     (1.5)

В природе чаще всего наблюдаются движения, в которых скорость изменяется как по величине (модулю), так и по направлению, т.е. приходится иметь дело с неравномерными движениями. Для характеристики изменения скорости таких движений вводится понятие ускорения.

     Пусть за время движущаяся точка перешла из положения А в положение В (рис. 1.4). Вектор   задает скорость точки в положении А. В положении В точка приобрела скорость, отличную от как по величине, так и по направлению и стала равной . Перенесем вектор в точку А и найдем .      Средним ускорением неравномерного движения в интервале времени от t до называется векторная величина, равная отношению изменения скорости к интервалу времени :

     (1.9)

     Очевидно, что вектор совпадает по направлению с вектором изменения скорости .      Мгновенным ускорением или ускорением материальной точки в момент времени t будет предел среднего ускорения:

     (1.10)

     Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.      Разложим вектор на две составляющие. Для этого из точки А по направлению скорости отложим вектор , по модулю равный . Тогда вектор , равный , определяет изменение скорости по модулю (величине) за время , т.е. . Вторая же составляющая вектора характеризует изменение скорости на время по направлению - .      Составляющая ускорения, определяющая изменение скорости по величине, называется тангенциальной составляющей . Численно она равна первой производной по времени от модуля скорости:

     (1.11)

         Найдем вторую составляющую ускорения, называемую нормальной составляющей. Допустим, что точка В достаточно близка к точке А, поэтому путь можно считать дугой окружности некоторого радиуса r, мало отличающегося от хорды АВ. Из подобия треугольников АОВ и ЕАD следует, что

     ,

     откуда В пределе при поэтому вторая составляющая ускорения равна:

     (1.12)

         Она характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории по нормали. Ее называют также центростремительным ускорением.      Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:

     (1.13)

     Из рис. 1.5 следует, что модуль полного ускорения равен:

     (1.14)

     Направление полного ускорения определяется углом между векторами и . Очевидно, что

     (1.15)

     В зависимости от значений тангенциальной и нормальной составляющих ускорения движение тела классифицируется по-разному. Если (величина скорости не изменяется по величине), движение является равномерным. Если > 0, движение называется ускоренным, если < 0 – замедленным. Если = const 0, то движение называется равнопеременным. Наконец, в любом прямолинейном движении (нет изменения направления скорости).      Таким образом, движение материальной точки может быть следующих видов:      1) - прямолинейное равномерное движение ( );      2) - прямолинейное равнопеременное движение. При таком виде движения

         Если начальный момент времени , а начальная скорость , то, обозначив и , получим:

3. Линейная скорость V=dr/dt=ωr. Вектор V направлен по правилу правого винта: из конца вектора V поворот вектора ω к r по кратчайшему расстоянию виден совершающимся против хода часовой стрелки. Угловая скорость тела равна отношению вектора элементарного поворота тела к продолжительности этого поворота: ω=dφ/dt. При неравномерном вращении тела вокруг неподвижной оси его угловая скорость изменяется. Вектор, характеризующий быстроту изменения угловой скорости тела, называется угловым ускорением: ε=dω/dt. Если тело вращается вокруг неподвижной оси ускоренно, то вектор ε направлен по оси вращения в ту же сторону, что и вектор ω. При замедленном вращении вектор ε направлен в сторону, противоположную вектору ω. Связь угловой скорости с линейной V=ωR(R-радиус кривизны). Поступательное движение – движение при котором прямая соединяющая любые две точки этого тела , перемещаясь вместе с телом, остаётся параллельной своему первоначальному положению(поршень в цилиндре двигателя, кабина шахтного подъёмника). Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

4. Сила- мера мех-го действия одного тела на другое (векторная величина). Мех-кое взаимодействие может осущ-ся как между контактирующими телами (при ударе, трении, давлении друг на др) так и между удаленными телами (притяжение планет к солнцу). Масса – мера инертности, «+»-ная скалярная величина, постоянна, независящая не от состояния движения тела, не от его места положения в пространстве. Поэтому для сравнения масс 2-х тел достаточно сравнить их ускорение (а = F/m). Вектор p, равный произведению массы материальной точки на ее скорость наз-ся импульсом (p = mV). Закон инерции: в инерциальной с-ме отсчета всякая материальная точка, неподверженная внеш. воздействиям, сохраняет свою скорость неизменной (1-ый закон Ньютона). Инерциальная с-ма отсчета – с-ма в к-рой выполняется 1-ый закон Ньютона. Свободная от внеш. воздействий материальная точка должна иметь равное нулю ускорение относительно всякой инерциальной с-мы отсчета. поэтому любые две инерциальные с-мы отсчета либо взаимно неподвижны, либо движутся друг относительно друга поступательно и при том равномерно и прямолинейно. Урав-е движения материальной точки: d(mV)/dt = F или F = md²r/dt². Закон динамики материальной точки: скорость изменения импульса матер-ой точки равна действующей на нее силе. Закон динамики с-мы матер-ных точек: две матер-ые точки действуют друг на друга силами, равными по модулю и направленными в противоположные стороны вдоль соединяющей эти точки прямой.

5. Внеш. тела – тела, невходящие в рассматриваемую механ-ую с-му. Следовательно, внеш. силы – силы действующие на тела с-мы со стороны внеш. тел. Внутр. силы – силы взаимодействия частей самой с-мы. F = F^внеш + Σ F_k, где F^внеш - результирующая всех внеш. сил, а F_k – внутр. сила. Так на замкнутую с-му внеш. силы не действуют, то выполняется закон сохранения импульса: импульс замкнутой с-мы не изменяется с течением времени: dp/dt = 0 и p=Σ mV = const. Соответственно не изменяются также и проекции импульса замкнутой с-мы на оси декартовых координат. Этот закон справедлив не только в рамках классической механики Ньютона (в равной мере справедлив для макроскопических с-м тел и для с-м макрочастиц, хотя последние описываются в квантовой механики), также закон выполняется и в релятивистской механике, т.е. независимо от того, велики или малы скорости тел или частиц, образующих с-му. При этом необходимо иметь в виду, что импульсом могут обладать не только частицы и тела, но и поля (давление электромагнитных волн, света на отражающие или поглощающие их препятствия). Однородность пространства проявляется в том, что законы движения и физ-кие св-ва замкнутой с-мы не зависят от выбора начала координат инерциальной с-мы отсчета, т.е. они не изменяются, если замкнутую с-му переставить в пространстве как целое путем параллельного переноса.

6. Реактивное движение – Векторная величина: F_p =u(dm/dt), где u – скорость истечения продуктов сгорания из сопла ракеты, измеренная относительно ракеты.

Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное Иваном Мещерским в 1904 году. Оно имеет вид:

,

где:

m — переменная масса тела;

v — скорость движения тела переменной массы;

F — внешние силы (сопротивление среды и т. п.);

u₁ — относительная скорость отделяющихся частиц;

u₂ — относительная скорость присоединяющихся частиц;

 — секундный расход массы;

 — секундный приход массы.

Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

,

где:

V — конечная (после выработки всего топлива) скорость летательного аппарата;

I — удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива);

M₁ — начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо).

M₂ — конечная масса летательного

7. Работой называется скалярное произведение F на dr: δA=Fdr=Fvdt, где r и v=dr/dt –радиус-вектор и скорость точки, dt-малый промежуток времени, в течении которого сила F совершает работу δА. Т.к. скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, то:δA=|F| |dr| cosα. Мощностью N силы называется соотношение элементарной работы dA, совершённой этой силой F за малый промежуток времени, к его длительности dt. N=dA/dt=Fdr/dt=FV, где V-скорость перемещения точки приложения силы. Кинетической энергия механич-ой с-мы наз-ся энергия механич-го движения этой с-мы. Изменение кинетич-й энергии материальной точки происходит под действием приложенной к ней силы F и равно работе, совершаемой этой силой dW = Fdr=FVdt, где V – скорость материальной точки.W = p²/2m = mV²/2, p - импульс материальной точки, а m- ее масса.

8. В зависимости от совершаемой работы все силы можно разделить на консервативные и неконсерватив-е. Конс. –наз-ся силы, работа к-рых не зависит от формы пути, а зависит только от начального и конечного положения тела (сила тяжести, упругости, гравитационного притяжения, электростатическая, др.) Неконсерв.-е силы, работа к-рых зависит от формы пути (сила трения, сопротивления (обе диссепативные, т.к. происходит переход энергии из одной в другую и рассеевает ее пространство), магнитные силы). С-мы материальных точек наз-ся консервативными, если в них действуют консерв-ые силы. С-мы мт наз-ся неконсерванивными, если в ней на ряду с консерв-ыми действуют неконсерват-е. С-ма м.т. наз-ся диссипативной если в ней действует дисстпативная сила на ряду с другими. Если действующая сила консерв-на, то поле потенциально. Если тело находится в потенц-ом поле, то оно обладает потенц-ной энергией. Под энергией – работа, совершаемая консерв-ной силой при перемещении из данного положения в нулевое (А=W(1)-W(2)). Потенциальная энергия  — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы.

9. а)З.сох.мех.энер.: мех. энергия конс-ной системы постоянна. Мех. система наз-ся конс-ной, если все действующие на нее внешние и внутренние непотенциальные силы не совершают работы, а все внешние потенциальные силы стационарны. б)Сумма пот-ной и кин-кой энергий тела есть полная мех-кая энергия. в)Общефиз. зак.: Энергия тела никогда не исчезает и не появляется вновь, она лишь переходит из одного вида в другой. Однородность пространства проявляется в том, что законы движения и физ. Св-ва замкнутой системы не зависят от выбора начала координат ИСО. 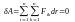,(dr-расстояние), а так как dr ≠0,то .Из этого соотношения следует закон сохранения импульса замкнутой системы. Изотропность пространства проявляется в том, что физ. св-ва и законы движения замкнутой системы не изменяются при ее повороте в пространстве как целого на любой угол, т.е. не зависят от выбора направления осей координат ИСО. Т.к. dφ≠0, то . r_i – радиус-вектор, проведенный в i-ую (.) системы из (.)О(начало координат).Из этого соотношения(полученного на основании 2-го з.Ньютона) следует з. сохранения момента импульса замкнутой системы. Однородность времени проявляется в том, что законы движения замкнутой системы не зависят от выбора начала отсчета времени: если в любые два момента времени замкнутую систему поставить в совершенно одинаковые условия, то начиная с этих моментов времени все процессы в системе будут протекать совершенно одинаково. Из однородности времени следует, что потенциальная энергия замкнутой системы не может зависеть явно от времени, т.е. изменяться с течением времени при условии неизменности конфигурации системы: .Поэтому, если в системе не действуют потенциальные силы или они не совершают работы, то согласно уравнению 11, механическая энергия такой замкнутой системы (консервативной)

не изменяется с течением времени. Симметрия: . Замена t на t’=-t и p на p’=-p, т.е. изменить направление хода времени, а также заменить на противоположное направление движения материальной точки: . Эта симметрия уравнений классической механики свидетельствует об обратимости механических процессов: если механическая система совершает какое-либо движение, то она может под действием тех же сил совершать и прямо противоположное движение, при котором эта система будет проходить через те же самые промежуточные конфигурации в обратном порядке.

10. Ударом наз-ся кратковременное взаимод-вие тел, в результате к-рого его скорость изменяется. Абсолютно упругий удар – взаимодействие, при к-ром имеет место только упругое взаимодействие тел, при этом нет механической энергии во внутр. и не действуют диссипативные силы. При упругом ударе тела после него имеют разные скорости. Выполняются законы сохранения импульса и механич-ой энергии. В процессе удара систему можно считать замкнутой и консервативной. Перед и после удара тела не деформируются, так что потенциальную энергию с-мы в этих двух состояниях можно считать одинаковой и =0. Абсолютно неупругий удар – это взаимодействие при к-ром имеет место неупругая деформация. После удара тела движутся как одно целое, т.е. с одинаковой скоростью. В процессе удара с-ма замкнутая и неконсерват-ная, следовательно, выполняется закон сохранения импульса и не выполняется закон сохранения энергии. Если скорости тел до удара равны V₁ и V₂, а их массы равны m₁ и m₂, то общая скорость поступательного движения этих тел после а.н.у. равны U= (m₁V₁) + (m₂V₂) / m₁+m₂. При а.у.у: U₁= (V₁(m₁-m₂)+ 2m₂V₂)/(m₁+m₂); U₂ = (V₂(m₂-m₁)+2m₁V₁) / (m₁+m₂).

11. В ньютоновской механике при переходе от одной инерциальной сис-мы отсчёта К (x,y,z,t) к другой К’(x’,y’,z’,t’), движущейся относительно К поступательно со скоростью V, пользуются преобразованиями Галилея .Механический принцип относительности Галилея: законы механики одинаковы во всех инерциальных системах отсчёта. 1)никакими механическими опытами проведёнными в замкнутой системе тел нельзя обнаружить движется эта система или покоится 2)все механические явления протекают совершенно одинаково во всех инерциальных системах отсчёта. Постулаты:1)а)принцип относительности: все физические явления при одних и тех же условиях протекают одинаково в любых инерциальных системах отсчёта; б)никакими опытами не обнаружить покоится система или движется; 2)постоянство скорости света: скорость света в вакууме –есть величина постоянная, не зависящая от скорости движения источника приёмника света.

Мы получили классический закон сложения скоростей (хорошо подтверждается при скоростях движения много меньше скорости света).

Формула читается так:

Скорость тела относительно неподвижной системы отсчета (результирующая) равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной.

12. Из постулатов спец-ной теории относительности, а также из однородности и изотропности пространства и однородности времени, следует, что соотношение меду координатами и временем одного и того же события в двух инерциальных с-мах отсчета выражаются преобразованиями Лоренца. Преобразования Лоренца имеют простейший вид в том случае, когда сходственные оси декартовых координат неподвижной (К) и движущейся (K’) инерциальных с-м попарно параллельны, причем с-ма К’ движется относительно К с постоянной скоростью V вдоль оси ОХ. Если кроме того в кач-ве начала отсчета времени в обеих с-мах (t=0 и t’=0) выбран тот момент, когда начала координат О и О’ обеих с-м совпадают, то преобразования Лоренца имеют след-ий вид: x’=(x-Vt)/ корень из (1-V² /c²); y’=y; z’=z; t’=(t-Vx/c²)/корень из (1-V²/c²); x=(x’+Vt’)/корень из(1-V²/c²);y=y’; z=z’ ;t=(t’+Vx’/c²) / корень из (1-V²/c²). Вывод: 1) преобразовываются не только координаты, но и время.2) Каждая новая более современная теория включает в себя старую как частный случай 3)при V→0, корень из (1-V²/c²)=1 и преобразования Лоренца переходят в преобразования координат Галилея.4) При V→с, корень из (1-V²/c²)→0 и преобразования Лоренца теряют смысл, значит скор. света недостижима и никакой объект не может двигаться со скоростью света. Одновременность: относительна одновременность двух событий, происходящих в разных точках пространства: события, одновременные в одной ИСО, не всегда одновременны в других ИСО, движущихся относительно первой. На рисунке достижение светом вспышки (.)А и В-события одновременные в неподвижной ИСО К(t₁=t₂), но совершающиеся в разных (.)(х_В=-х_А).В движущейся К’ они не одновременны(формула). В (.)А свет позже попадает из О’, чем в В, приближающуюся в О’ .

13. Из преобразований Лоренца следует, что линейный размер, размер тела движущегося относительно инерциальной с-мы отсчета, уменьшается в направление движения. Это изменение продольного размере тела при его движении наз-ся Лоренцевым сокращением. Пусть l₀ – длина стержня, покоящегося в с-ме K’. Если стержень расположен вдоль оси О’X’, то l₀= x₂’-x₁’, где x₂’,x₁’, - координаты концов стержней. Длина l того же стержня в с-ме отсчета К, относительно к-рой он движется вдоль оси ОХ со скоростью V, равна разности значений координат концов стержня, измеренных в один и тот же момент времени t: l=x₂(t)-x₁(t)= (x₂’-x₁’)*корень из (1-V²/c²)=l₀*корень из (1-V²/c²).Линейные размеры тела относительны. Они максимальны в той инерциальной сис-ме отсчёта, относ. кот. тело покоится. Эти размеры тела называются его собственными размерами.Ещё одним следствием преобр. Лоренца явл. относит-ть промежутка времени между какими либо событиями.τ=(t₁’-t₂’)/корень из (1-V²/c²)=τ₀/корень из(1-V²/c²), где τ₀₌t₂’- t₁’.Промежуток времени между двумя событиями минимален в той инерциальной сис-ме отсчёта, относит. Которой оба события происходят в одной и той же точке. Время, измеряемое по часам, движущимся вместе с данным объектом наз-ся собственным временем этого объекта. Рассмотренная закономерность свидетельствует о существовании релятивистского эффекта замедления хода времени: часы, движущиеся со скоростью V относительно данной инерциальной системы отсчёта, идут медленнее в корень из 1/(1-V²/c²) раз, чем неподвижные. Все физ. процессы в движущейся системе отсчёта протекают медленнее, чем в неподвижной.

14.Значения V и V’ скорости точки в двух инерциальных системах отсчёта К и К’ равны V=dr/dt=v_xi+v_yj+v_zk, V’=dr’/dt’=v’_xi’+v’_yj’+v’_zk’, где r=xi+yj+zk и r’=x’i’+y’j’+z’k’ –радиусы-векторы рассматриваемой точки в системах отсчёта К и К’. Проекции скоростей V и V’ на оси декартовых координат: v_x=dx/dt, v_y=dy/dt, v_z=dz/dt; v’_x’=dx’/dt’(для y,z – т.ж.). Если сходственные оси декартовых координат систем отсчёта К и К’ попарно параллельны и система К’ движется относительно К с пост. скоростью V, направленной вдоль оси ОХ, причём в момент начала отсчёта времени в К и К’ (t=t’=0) начало координат О и О’ этих систем совпадают, то справедливы преобразования Лоренца в форме: x’=(x-Vt)/ корень из (1-V² /c²); y’=y; z’=z; t’=(t-Vx/c²)/корень из (1-V²/c²); x=(x’+Vt’)/корень из(1-V²/c²);y=y’; z=z’ ;t=(t’+Vx’/c²) / корень из (1-V²/c²). Из этих преобразований следует, что dx’/dt=(dx/dt-V)/ корень из (1-V/c)=v_x-V/ корень из (1-V/c), dy'/dt=dy/dt=v_y , dz’/dt=v_z , dt’/dt=(1-Vv_x/c² )/ корень из (1-V/c). Т.к. v’_x’=dx’/dt’=(dx’/dt) : (dt’/dt), (для y,z-так же), то связь между проекциями скоростей точки на оси декартовых координат в системах отсчёта К и К’ имеет вид: v’_x’=(v_x-V)/1-Vv_x/c², v_x=(v’_x’+V)/1+Vv’_x’/c², v’_y’=(v_y*корень из(1-V²/c²))/ 1-Vv_x/c², v_y=(v’_y’*корень из(1-V²/c²))/ 1+Vv’_x’/c², v’_z’=(v_z*корень из (1-V²/c²))/1-Vv_x /c², v_z=(v’_z’*корень из (1-V²/c²))/1+Vv’_x’ /c².Эти формулы выражают закон сложения скоростей в релятивистской кинематике. В пределе при с→∞ они приводят к обычному закону сложения скоростей в классической механике Ньютона: v’_x’= v_x-V (для y,z-т.ж.) и v’=v-V.

15. Релятивистской динамикой называется динамика движений с релятивистскими скоростями основанная на спец. теории относительности. Релятивистскими скоростями называются скорости движения тел близкий к скорости в вакууме. Релятивистский импульс: р=mv, m=m₀/корень из(1-V²/c²),p= m₀v/ корень из(1-V²/c²), где m₀-масса покоя. Основное уравнение релятивистской динамики материальной точки имеет вид: d/dt*(mv/корень из(1-V²/c²))=F или dp/dt=F. Кин.энергия(T). Приращение кин. энергии мат. точки на элементарном перемещении dr равно работе совершаемой на этом перемещении силой F действующей на материальную точку: dT=Fdr=Fvdt, где v-скорость точки. ΔT=T=(m₀c²/(1-V²/c²))- m₀c². T=mc²-m₀c² . E= mc², E₀= Δ (энергия покоя). Кинетическая энергия в СТО равна разности полной энергии и энергии покоя. T= m₀c² *(1/ корень из(1-V²/c²)-1). Формула выражающая взаимосвязь энергии покоя и массы покоя: Δ E₀= Δ m₀c².

16. Закон взаимосвязи массы и энергии: энергия покоя сис-мы равна произведению массы этой сис-мы на квадрат скорости света в вакууме: ∆E₀=∆m₀c².Связь между импульсом и полной энергии: p=m₀v/ (корень из(1-β²)), E=m₀c²/ (корень из (1-β²)), p/E= v/c², следов-но v=pc²/E.

v²=(p²c⁴)/E²; E²=m₀²c⁴/ (1-v²/c²) | *(1-v²/c²) E²-E²v²/c²=m₀²c⁴; в данную формулу подставим v² и получим: E2 - (E²p²c⁴²)/E²c²=m₀²c⁴; E²-m₀²c⁴=p²c²,

E² = p²c²+m₀²c⁴, E=c*(корень из(p²+m₀²c²)), p²c²=E²-m₀²c⁴; p=1/c *(корень из(E²-m₀²c⁴))

Релятивистской энергией и релятивистским импульсом . При переходе из одной инерциальной системы отсчета в другую значение каждой из четырех компонент 4-импульса определяется по формулам Лоренца через все четыре компоненты в исходной системе I. Например, значение энергии в системе II определяется не только через энергию в системе I, но и через все компоненты импульса .

     Полезными являются также очевидные формулы для релятивистского импульса и его модуля в виде:

17. Границы применимости классической механики:

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)

При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.

Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

18. Моментом силы наз-ся векторное произведение радиуса-вектора r на приложенную силу F. Вектор М = вектор r умножить на вектор F. Вектор М – направлен перпендикулярно плоскости векторов r и F по правилу правого винта. М=Frsinα = Fl, где α – угол между r и F, l=rsinα – длина перпендикуляра, - плечо силы

М F

α

r

О 90º l

Моментом импульса L относительно точки наз-ся векторное произведение радиуса-вектора на импульс

Вектор L =| вектор r * вектор р|; L=rpsinα . Закон изменения момента импульса: dL/dt=M ^внеш. Закон сохранения момента импульса: Σ Iω = const. Моментом импульса относительно оси наз-ся проекция вектора L относительно точки на данную ось.

19. Уравнение динамики вращательного движения тела относит-но оси имеет вид: dL/dt = M^внеш, L –момент импульса. Величина J равная сумме произведений масс m_i всех материальных точек, образующих механ-кую с-му на квадрат расстояний R_i от данной оси, наз-ся моментом инерции с-мы отсительно этой оси: Σm_iR_i². Подсчитать момент инерция тела можно с помощью теоремы Штейнера: момент инерции J_a тела относительно произвольной оси а = сумме моментов инерции J_c тела относит-но параллельной ей оси а_с, проходящей через центр масс С тела, и произведения массы тела m на квадрат расстояния d между этими осями: J_a = J_с +md². Момент инерции тела зависит от материала, формы и размеров тела, а также от расположения тела относит-но оси.

20. Для замкнутой с-мы момент внеш. сил всегда =0, т.к. на нее внеш. силы не действуют. Поэтому из законе изменения момента импульса (dL/dt =M^внеш) вытекает след-ий закон, назыв-мый законом сохранения момента импульса: момент импульса замкнутой с-мы не изменятся с течением времени (dL/dt=0 и L=const). Изотропность пространства проявл-ся в том, что физ-кие св-ва и законы движения замкнутой с-мы не изменяются при ее повороте в пространстве как целое на любой угол, т.е. не зависит от выбора направления осей координат инерциальной с-мы отсчета. Моментом импульса механич-кой с-мы относительно оси наз-ся проекция на эту ось вектора момента импульса с-мы относительно любой точки, выбранной на рассматриваемой оси dL_x/dt=M_x^внеш, аналог-но y,z. Уравн-я справедливы также для моментов импульса с-мы и внеш. сил относительно неподвижной точки О. Условие сохранения момента импульса незамкнутой с-мы относительно оси: если момент относительно какой-либо неподвижной оси всех внеш. сил, действующих на с-му, тождественно = 0, то момент импульса с-мы относительно этой оси не изменяется с течением времени.

21.Все системы отсчёта делятся на два типа:1.Инерциальные-1)З-ны Ньютона выполняются.2)Они покоются или движутся V=const (a=0).3)Нет сил инерции.2Неинерциальные-1)З-ны Ньютона не выполняются. 2)Vconst,a.3)Существуют силы инерци.

Производная массы на ускорение в системе К и К’ различны, они отличаются на некоторую величину mR,имеющую размерность MLT^-2 –силы, называемой силой инерции. Сила инерции - это сила не обусловленная взаимодействием с другими телами ,но обусловлена ускорением систем силы инерции существ-их только в тех системах, которые движ-ся сaми. Св-ва сил инерции в поступательном движении:1)F_ин не обусловлена взаимодействием с другими телами.2)F_ин  a_с 3)F_ин =масса тела на ускорение сист. 4)Внешние силы всегда являются внешними по отношению к данной системе.

22. Шарик массой m движ. с пост. скор. u’ вдоль радиуса равномерно вращ-ся диска (u’=const, =const, u’). Если диск не вращ. То шарик при движ. попадает в т.A, а если вращ. – то в т.В, причём его скорость u’ относит. Диска изм-ет своё направление. Это возможно, если на шарик действует сила перп. u’. Если заставить шарик катиться прямо (вдоль стержня ОА), тогда при отклонении шарика стержень действ. на него с некот. силой F. Относит. диска шарик движется равномерно и прямолинейно, что объясняется тем, что сила F уравновеш-ся приложенной к шарику силой F_K, перп-ой скор-ти u’. Эта сила назыв. кориолисовой силой инерции. F_K = 2m[u’]. Вектор F_K перп-рен скор-ти u’ и угловой скор-ти вращения  системы отсчёта в соотв. с правилом правого винта. Сила Кориолиса действует только на тела, движ-ся относительно вращ-ся систем отсчёта.

23.Физические свойства макроскоп-х сис-м, состоящих из очень большого числа частиц, изучаются 2-мя методами: статистическим (Ст) и термодинамическим (Тер). Ст. метод основан на использовании теории вероятностей и определенных моделей строения изучаемых систем. Н-р, в газе можно определить средние значения скоростей теплового движения молекул и их энергий, связанных с температурой газа. Тер. метод основан на анализе условий и колич-ных соотношений при различных превращениях энергии, происходящих в системе. Соотношения между разными видами энергии позволяют изучать физические св-ва исследуемых систем при самых разнообразных процессах, в к-рых эти с-мы участвуют. Раздел теоретической физики, в котором физич. св-ва макроскоп-х сис-м изучаются с помощью термодин-го метода называется термодинамикой. Мысленно выделенная макроскоп. система, рассмат-мая методами термодинамики наз-ся термодинамической с-мой (тс). В завис-ти от возможных способов изоляции сис-мы от внешней среды различ-т неск-ко видов тс. Открытая тс –может обмениваться вещ-вом с внеш. средой(все жив организмы).Закрытая-не может. Изолированная- не обмен-ся с внеш. средой ни энергией, ни вещ-вом. Замкнутая-не способна к обмену энергией с внеш.средой путём соверш. работы(газ в сосуде пост.объёма). Адиабатная-не обмен-ся с др. сис-ми энергией путём теплообмена. Особенности теплового движения в 3-х агрегатных состояниях связаны с тем, что между молекулами действуют силы взаимного притяжения и отталкивания. Они проявляют себя тем в большей степени, чем меньше среднее расстояние между молекулами. Молекулы движутся прямолинейно и равномерно до тех пор, пока не происходят столкновения их между собой или со стенками сосуда, в к-ром нах-ся газ. Ид-м наз-ся газ, молекулы к-го имеют пренебрежимо малый собственный объем и не взаимод-ют друг с другом на расстоянии. Даже простейшие по своим св-вам газы лишь приближенно могут считаться ид-ми. Модель идного газа позволяет изучать св-ва газов в кинетической теории простейшим образом. Ур-ние, связывающее любой термодинам-кий параметр с-мы с параметрами, принятыми в кач-ве независимых переменных, наз-ся ур-нием состояния. термическое ур-ние состояния ид-го газа, наз-ся ур-нием Клапейрона: pV/T=C=const. Ур-е сост. ид. газа:PV=mRT/μ.Если параметры p,V,T имеют одинак. знач-е во всей с-ме – то состояние равновесное. Релаксация – переход из неравновесного состояния в равновесное.Закон Дальтона для давления смеси газов: p=Σp_i,где p_i-парциальное давление, т.е. давление которое имел бы каждый из газов в отдельности, если бы при данной температуре он заполнял весь объём.Изот.процесс(T-const)Изохор.(V-const)Изобар.(p-const)адиабат.(нет теплообмена между сис-мой и внеш. средой).

24. Для вывода осн. ур-я МКТ рассмотрим ид. газ. Молекулы газа движ. хаотично, число взаимных столкновений между молек. газа пренебрежимо мало по сравн-ю с числом ударов о стенки сосуда, а соударения со стенками сосуда абс. упр. Выделим на стенке сосуда некоторую элементарную площадку S. и вычислим давление на эту площадку. При каждом соударении молекула, движ. перп. площадке, передаёт ей импульс m₀u-(-m₀u)=2m₀u, где m₀ – масса молек., u – её скор. За время t площадки S достигнут только те молекулы, которые заключены в объёме цилиндра с осн. S и высотой ut. Число этих молекул равно nSut. (n – конц. молекул). Необх. учитывать, что реально молекулы движ. к площадке S под разными углами и имеют различные скорости, причём скорость молекул при каждом соударении меняется. Для упрощ. расчётов хаотич. движ. молекул замен. движ-ем вдоль трёх взаимно перп. направлений, так что в люб. момент времени вдоль кажд. из них движ. 1/3 молекул, причём одна половина (1/6) движ. в одну, а другая в противоп. сторону. Тогда число молекул, движ-ся в заданном направлении, о площадку S, будет 1/6nSut. При столновении с площадкой эти молекулы передадут ей импульс P=2m₀u*1/6nSut=1/3nm₀u²St. Тогда давл. газа на ст. сосуда p=P/(St)=1/3 nm₀u² Если газ в объёме V содерж. N молекул, движ-ся со скор-тями u₁, u₂,..,u_N, то целесообр. рассм. среднюю квадр. скорость.(см 25). Тогда осн. ур-е МКТ идеальных газов примет вид: p = 1/3 n m₀<U_кв>² (где <U_кв>² – средняя квадратичная скорость.) p=2/3n<E>.

Это выражение объясняет молекулярно-кинетический смысл понятия температуры. Температура – это средняя кинетическая энергия движения молекул (выраженная в других единицах).

Давлением газа с точки зрения МКТ считается импульс, переданный по площади за единицу времени: p = 1/3 n m₀ U²

25. Функция распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные du, то на каждый интервал скорости будет приходиться некоторое количество молекул dN(u), имеющих скорость, заключённую в этом интервале:

Функция для распределения молекул идеального газа по скоростям:

Конкретный вид функции зависит от рода газа.

Функция распределения молекул по энергиям теплового движения.

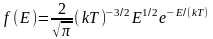
Наиболее вероятная скорость – скорость, при которой функция распределения молекул идеального газа по скоростям максимальна.

Средняя скорость молекулы (средняя арифметическая):

Средняя квадратичная скорость:

26. В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

n = n₀exp( -mgh / kT )

где n - концентрация молекул на высоте h, n₀ - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.

Анимация показывает схематически движение молекул газа в присутствии гравитационного поля. Мы можем видеть, что концентрация молекул у дна сосуда оказывается выше, чем концентрация в верхней части сосуда. Под действием теплового движения молекулы подбрасываются вверх, а затем падают вниз за счет действия сил тяжести.

Если высота сосуда много меньше чем kT/mg, то зависимостью концентрации от высоты можно пренебречь. С другой стороны, в атмосфере концентрация молекул быстро уменьшается с увеличением высоты и, поэтому, величина атмосферного давления также уменьшается. Принимая во внимание, что P = nkT, мы можем записать так называемую барометрическую формулу, описывающую изменение атмосферного давления в зависимости от высоты:

P = P₀exp( -mgh / kT )

Измеряя давление за бортом самолёта, мы можем вычислить при помощи барометрической формулы приблизительную высоту полёта.

27. Работа -Энергия, передаваемая рассматриваемой термодинамической сис-ме внешними телами путём совершения работы, называется работой, совершаемой над системой. Теплота -Энергия, передаваемая системе внешними телами путём теплообмена, называется теплотой, получаемой системой от внешней среды.Работу над сис-мой производят внешние силы. Для совершения работы над макроскопически неподвижной с-мой нужно, чтобы изменялись внеш. параметры состояния с-мы. В отсутствие внеш. силовых полей обмен энергией между неподвижной с-мой и внеш. средой может осущ-ся путем совершения работы лишь в процессе изменения объема и формы с-мы. Теплообмен происходит между телами или частями одного и того же тела нагретыми до различной температуры. Три вида теплообмена: 1) конвективный (в батарее водяного отопления от более горячей воды энергия передается к менее нагретым стенкам), 2) теплопроводность (передача теплоты через стенку батареи от более нагретой внутр. пов-ти к менее нагретой наружн. пов-ти), 3) теплообмен излучением (происходит за счет испускания и поглащения электромагнитного излучения). Понятие теплоты и работы имеют смысл только в связи с процессом изменения состояния с-мы. Они явл-ся энергетич-ми хар-ми этого процесса. Часто оба способа передачи энергии осущ-ся одновременно. Н-р, при нагревании газа в сосуде с неподвижным поршнем газу сообщается теплота и происходит увеличение его объема. При этом соверш-ся работа против внеш. давления.1-ое начало термодинамики: теплота сообщаемая с-ме расходуется на изменение внутр. энергии с-мы и на совершение с-мой работы против внеш. сил (δQ=dU+δA). При изохорном процессе δQ=dU, т.к. газ не совершает работы над внеш.силами. При изотермическом: δQ=δА (внутр. энергия не измен-ся, dU=0). При адиабатном: dU= -δA, т.к δQ=const.

28. Теплоемкостью наз-ся физ-кая величина, численно равная отношению теплоты δQ, сообщаемой газу, изменению dT температуры тела, в рассматриваемом термодинамич-ом процессе: С = δQ/dT. Теплоемкость зависит от химич-го состава, массы и термодинамического состояния, а также от вида процесса изменения состояния тела в к-ром поступает теплота δQ. Тепловые св-ва однородных тел хар-зуются значениями удельной и молярной теплоемкости. Молярной теплоем-ю наз-ся физ-кая величина С численно равная теплоте к-рую нужно сообщить 1-му молю вещ-ва для изменения его температура на 1К в рассматриваемом термодин-ом процессе: С_m= Мс=МδQ/mdT, где М – молярная масса вещ-ва, с – его удельная теплоемкость. с=δQ/mdT. Классический статистический метод изучения тепловых св-в вещ-в позволил теоретически вычислить теплоемкость газов и твердых тел. Изохорный (V=const) процесс С_mV=iR/2; i=3 (одноатомный), i=5 (двухатомный). Изобарный (р=const): с_mp= ((i+2)R) /2. Уравн-е Майера: С_p-C_v = R.

29. Адиабатный процесс – термодинамический процесс, в котором система не обменивается теплотой с окружающей средой (δQ=0). Практически процесс осуществляется при достаточно быстром расширении или сжатии газа. Из первого начала термодин-ки:δA=-dU, т.е. в адиабатном процессе система совершает работу за счёт убыли вн. энергии сис-мы. Если газ ад.расшир-ся, то δA=pdV>0 и dT<0, т.е. происх.охлаждение газа. При адиаб.сжатии газ нагревается, т.к. δA<0 и dT>0. C=δQ/dT. pV^γ =const –Уравнение Пуассона, где γ-безразмерная величина-покзатель адиабаты или коэффиц. Пуассона γ=С_P/ C_V (для любого идеального газа γ>1).При помощи ур-я Клап.-Мендел. ур-е Пуассона можно записать в виде связи между др. параметрами сост.газа в адиаб.процессе:pT^γ/(γ-1)=const VT^1/(γ-1)=const.Работа, совершаемая при адиабатном процессе может быть найдена по формуле A=(RT₁m/(γ-1)μ)*(1-(V₁/V₂)^γ-1) =(RT₁m/ (γ-1)μ)*(1-T₂/T₁)=p₁V₁(T₁-T₂)/(γ-1)T₁.

30.Политропный процесс- термодинамический процесс, описываемый уравнением pVⁿ=const, где n-безразмерная постоянная величина,называемая показателем политропы.При n=0-изобар.процесс, n=1-изотерм., n=γ-адиаб.,n=±∞-изох. Молярная теплоёмкость С ид. газа в политр.процессе: С=С_V+M_PdV/mdT. С_P=γR/γ-1. C_T=±∞. C_V=R/γ-1.C_адиаб=0

В зависимости от процесса можно определить значение n:

1. Изотермический процесс: n = 1, так как PV¹ = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV⁰ = P = const.

3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона.

4. Изохорный процесс: , так как , значит P₁ / P₂ = (V₂ / V₁)ⁿ, значит V₂ / V₁ = (P₁ / P₂)^{(1 / n)}, значит, чтобы V₂ / V₁ обратились в 1, n должна быть бесконечность.

31. Термодинамической вероятностью(статистический вес) называется то число микросостояний, которое может быть реализовано данное состояние. W=ωP, W- вероятность какого либо состояния тела (или системы), ω-вероятность отдельного распределения, Р-термодинамическая вероятность состояния. Термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать. Флуктуациями называются процессы самопроизвольного изменения параметров состояния в объёмах, малых по сравнению со всей системой. Если L-значение флуктуации в данный момент, <L>-её среднее значение, то разность ΔL=L-<L>, а также среднее значение <ΔL> не могут служить количественной мерой флуктуаций величины L, т.к. <ΔL> = <(L-<L>)>=<L>-<L>=0. Квадратичная флуктуация(дисперсия) : σ²_L=<ΔL²>=<(L-<L>)²>=<L²>-(<L>)². Абсолютная флуктуация σ _L= корень из <(L)²>. Относительная флуктуация: δ_L=σ_L/<L>= (корень из <(L)²>)/<L>.

32.Энтропия явл. одной из функций состояния термодин. сис-мы. Пусть δQ-элементарное количество теплоты сообщаемое нагревателем системе при малом изменении её состояния, а Т-t-ра нагревателя. Если процесс обратимый то t-ра сис-мы тоже равна Т. В отличии от δQ отношение δQ/Т в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией S cис-мы: dS= (δQ/Т)_обр.Из этого выражения видно что dS и δQ имеют один и тот же знак. Это позволяет по характеру изменения энтропии судить о направлении процесса теплообмена. При нагревании тела δQ>0 и его энтропия возрастает (dS>0), при охлаждении δQ<0 и энтропия тела убывает (dS<0). В обратимом адиабатном процессе δQ=TdS=0, так что dS=0 и S=const. Т. обр., обратимый адиабатный процесс представляет собой изоэнтропийный процесс. Энтропия, подобно внутренней энергии, аддитивная функция состояния с-мы: энтропия с-мы = сумме энтропий всех тел, входящих в состав с-мы. В термодинамике доказ-ся, что энтропия изолированной с-мы в любом обратимом процессе не изменяется. Дело в том, что при передаче теплоты δQ от тела 1 к телу 2 в обратимом процессе температуры обоих тел одинаковы. Поэтому изменение dS2 энтропии тела 2, получающего теплоту δQ, равно и противоположно по знаку изменению dS1 энтропии тела, отдающего теплоту δQ: dS= dS2 + dS1 =0.

33. 2-е начало термодинамики: 1)невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему; 2)невозможен процесс, единственным результатом которого является совершение работы за счёт охлаждения одного тела.Этот закон привёл к выводу о невозможности построения двигателя второго рода. Существует ещё одна формулировка: энтропия изолированной сис-мы не может убывать при любых происходящих в ней процессах: dS≥0, где знак рав-ва относ-ся к обратимым процессам, а знак больше-к необратимым. Из определения энтропии следует, что кол-во теплоты сообщаемое телу при малом обратимом изменении его состояния,δQ=TdS, где Т-температура тела. При необратимом процессе δQ<TdS, где Т-температура того «источника теплоты», который сообщает телу кол-во теплоты δQ в процессе малого необратимого изменения состояния этого тела.Неравенство TdS=dU+δA, объединяет оба закона термодинамики и является её важнейшим соотношением.

Основное термодинамическое тождество

Доказательство:

Первое начало термодинамики δQ = dU + δA можно записать в виде одного якобиана:

  Это равенство можно переписать в виде

         Обозначим:  , где F – разность двух функций состояний, поэтому сама является также функцией состояния. Ее назвали свободной энергией.        Тогда

         Если тело совершает обратимый изотермический процесс, то

 

         т.е. . Следовательно, свободная энергия есть та работа, которую могло бы совершить тело в обратимом изотермическом процессе, или свободная энергия есть максимальная возможная работа, которую может совершить система, обладая каким-то запасом внутренней энергии. Внутренняя энергия системы U равна сумме свободной (F) и связанной энергии (TS):

         Связанная энергия – та часть внутренней энергии, которая не может быть превращена в работу, – это обесцененная часть внутренней энергии.        При одной и той же температуре связанная энергия тем больше, чем больше энтропия.        Таким образом, энтропия системы есть мера обесцененности ее энергии (т.е. мера той энергии, которая не может быть превращена в работу).        В термодинамике есть еще понятие – энергетическая потеря в изолированной системе:

  где Tмин - температура окружающей среды.

       При любом необратимом процессе энтропия увеличивается до того, пока не прекратятся какие-либо процессы, т.е. пока не станет F = 0. И это произойдет при достижении замкнутой системой равновесного состояния, т.е. когда все параметры состояния системы (Р, Т) во всех точках системы станут одинаковыми. Вывести систему из этого равновесного состояния, можно только затратив энергию извне.

34. Основываясь на втором начале термодинамики, Карно вывел теорему: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т₁) и холодильников (Т₂), наибольшим КПД обладают обратимые машины(основанные на обратимых процессах); при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей (Т₁) и холодильников (Т₂), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами.)

Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат, и называемый циклом Карно.

Изотерм. расширение 1-2 и 3-4. Адиаб. сж. и расшир. 2-3 и 4-1

При изотерм. проц. 1-2 U=const поэтому A₁₂ = (m/M) RT₁ ln (V₂/V₁) = Q₁

При адиабатич. расшир. 2-3 теплообмен с окружающей средой отсутствует и работа расширения соверш. за счёт изм. внутр. энергии A₂₃= - (m/M) C_v (Т₂ - Т₁)

При изотермич. сжатии 3-4 кол-во теплоты Q₂, отданное газом хол-ку при изотерм. сжатии, равно работе сжатия: A₃₄= (m/M) RT₂ ln (V₄/V₃) = - Q₂

Работа адиабатич. сжатия: А₄₁ = - А₂₃

Работа, совершаемая в рез-те кругового процесса: А= A₁₂+ A₂₃+ A₃₄+ A₄₁= Q₁+ A₂₃ - Q₂ - A₂₃ = Q₁ - Q₂ и определяется площадью фигуры, ограниченной изотермами и адиабатами.

Термический КПД цикла Карно η =А/ Q₁=(Q₁ - Q₂)/ Q₁

Подставляя A₁₂ и A₃₄ в формулу η =А/ Q₁ получаем η =(T₁ - T₂)/ T₁

Т.е. для цикла Карно КПД определяется только температурами нагревателя и холодильника.

35. Беспорядочность теплового движения молекул газа, непрерывные столкновения между ними приводят к постоянному перемешиванию частиц и изменению их скоростей и энергий. Если в газе существует пространственная неоднородность плотности, t-ры или скорости упорядоченного перемещения отдельных слоёв газа, то происходит самопроизвольное выравнивание этих неоднородностей. В газе возникают потоки энергии, вещества, а т.ж. импульа упорядоченного движения частиц. Эти потоки, характерные для неравновесных состояний газа, являются физической основой особых процессов, названных явлением переноса. К этим процессам относятся: теплопроводность, внутреннее трение и диффузия. Диффузия (лат. diffusio — распространение, растекание, рассеивание) — процесс переноса материи или энергии из области с высокой концентрацией в область с низкой концентрацией (против градиента концентрации). Самым известным примером диффузии является перемешивание газов или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: если один конец стержня нагреть или электрически зарядить, распространяется тепло (или соответственно электрический ток) от горячей (заряженной) части к холодной (незаряженной) части. В случае металлического стержня тепловая диффузия развивается быстро, а ток протекает почти мгновенно. Если стержень изготовлен из синтетического материала, тепловая диффузия протекает медленно, а диффузия электрически заряженных частиц — очень медленно. Диффузия молекул протекает в общем ещё медленнее. Например, если кусочек сахара опустить на дно стакана с водой и воду не перемешивать, то пройдёт несколько недель, прежде чем раствор станет однородным. Ещё медленнее происходит диффузия одного твёрдого вещества в другое. Например, если медь покрыть золотом, то будет происходить диффузия золота в медь, но при нормальных условиях (комнатная температура и атмосферное давление) золотосодержащий слой достигнет толщины в несколько микрометров только через несколько тысяч лет. Коэффицие́нт диффу́зии — количество вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1 м²) при градиенте концентрации, равном единице (соответствующем изменению 1 моль/л → 0 моль/л на единицу длины). Коэффициент диффузии отражает скорость диффузии и определяется свойствами среды и типом диффундирующих частиц. Зависимость коэффициента диффузии от температуры выражается следующим уравнением: D = D₀exp( − E_a / kT)=1/3<v><l>( средняя длина свободного пробега молекул), где D — коэффициент диффузии [ {м²}/{сек} ]; E_a — энергия активации [Дж]; k — постоянная Больцмана; T — температура [⁰K].

36. Потоки (энергии, вещ-ва, импульса упорядоченного движения частиц), хар-ные для неравновесных состояний газа явл-ся физ-кой основой процессов названных явлением переноса. К этим явлениям относятся теплопроводность, вязкость, диффузия (см.35). Теплопроводность – явление возникающее при наличии разности температур, вызванной какими-либо внеш. причинами. При этом молекулы газа в разных местах его объема имеют разные средние кинетические энергии и хаотическое тепловое движение молекул приводит к направленному переносу внутр. энергии газа. Вязкость (внутр. трение) – явление связанное с возникновением сил трения между слоями газа, перемещающимися параллельно друг другу с различными по модулю скоростями. Закон Фурье q_сек =δQ/dSdt = - KdT/dx, где q_сек – плотность теплового потока, δQ – кол-во теплоты, к-рое передается в следствии теплопроводности за время dt через площадку dS, расположенную перпендикулярно направлению переноса внутр. энергии, К – коэффициент теплопроводности. Закон Ньютона (для вязкости) τ= ηdV/dn=dF/dS, где τ – напряжение трения, dF- касательная сила трения, действующая на пов-ть слоя площадью dS, а dV – изменение скорости течения газа (жидкости) на расстоянии dn в направлении внеш. нормали n к пов-ти слоя. Если τ<0, то η – динамическая вязкость. Кинематическая вязкость: ν = η/ρ, где ρ – плотность жидкости (газа). Сила вязкого трения

Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.

Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя. Это отличает вязкое трение от сухого.

[править] Вторая вязкость

Вторая вязкость, или объёмная вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

[править] Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где  — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность ρ прямо пропорциональна давлению, а - обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов,например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа u, растущей с температурой как

[править] Вязкость жидкостей

[править] Динамическая вязкость

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:

Коэффициент вязкости η (динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:

η = Ce^{w / kT}

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества V_M. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

[править] Кинематическая вязкость

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

и эта величина получила название кинематической вязкости. Здесь ρ, - плотность жидкости; η - динамическая вязкость (см. выше).

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В систему СИ эта величина переводится следующим образом:

1 сСт = 1мм² / 1c = 10 ^{− 6} м² / c

Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.

Для двухфазных жидкостей характерно свойство тиксотропии.

37. Фаза-совокупность всех частей системы, обладающих одинаковым хим. составом, находящихся в одинаковом состоянии и ограниченных поверхностями раздела. Фазовый переход- переход из одного состояния в другое.1-го рода: у в-ва изменяются плотность, молярный и удельный V, концентрации компонентов, выделяется теплота-теплота фазового перехода.(Испарение, конденсация). 2-го рода: теплота фазового перехода =0, плотность изменяется непрерывно, скачкообразно изменяются молярная теплоемкость, коэффициент теплового расширения, удельная электрическая проводимость, вязкость и др. (Переход магнитного вещества из ферромагнитного состояния в парамагнитное при нагреве до определенной температуры((.)Кюри)). 37.  

Условие равновесия фаз

Рассмотрим химически однородную систему (состоящую из частиц одного типа). Пусть в этой системе имеется граница раздела между фазами 1 и 2. Как было указано выше, для равновесия фаз требуется равенство температур и давлений на границе раздела фаз. Известно (см. статью Термодинамические потенциалы), что состояние термодинамического равновесия в системе с постоянными температурой и давлением соответствует точке минимума потенциала Гиббса.

Потенциал Гиббса такой системы будет равен

,

где μ₁ и μ₂ — химические потенциалы, а N₁ и N₂ — числа частиц в первой и второй фазах соответственно.

При этом сумма N = N₁ + N₂ (полное число частиц в системе) меняться не может, поэтому можно записать

.

Предположим, что , для определенности, . Тогда, очевидно, минимум потенциала Гиббса достигается при (все вещество перешло в первую фазу).

Таким образом, равновесие фаз возможно только в том случае, когда химические потенциалы этих фаз по разные стороны границы раздела равны:

.

Уравнение Клапейрона — Клаузиуса

Основная статья: Уравнение Клапейрона—Клаузиуса

Из условия равновесия фаз можно получить зависимость давления в равновесной системе от температуры. Если говорить о равновесии жидкость — пар, то под давлением понимают давление насыщенных паров, а зависимость P = P(T) называется кривой испарения.

Из условия равенства химических потенциалов следует условие равенства удельных термодинамических потенциалов:

,

где , G_i — потенциал Гиббса i-й фазы, m_i — её масса.

Отсюда:

,

а значит,

,

где v₁ и s₁ — удельные объем и энтропия фаз. Отсюда следует, что

,

и окончательно

,

где q — удельная теплота фазового перехода (например, удельная теплота плавления или удельная теплота испарения).

Последнее уравнение называется уравнением Клапейрона — Клаузиуса.

Тройна́я то́чка — точка на фазовой диаграмме, где сходятся три линии фазовых переходов. Тройная точка — это одна из характеристик химического вещества. Обычно тройная точка определяется значением температуры и давления, при котором вещество может равновесно находиться в трёх (отсюда и название) агрегатных состояниях — твёрдом, жидком и газообразном. В этой точке сходятся линии плавления, кипения и сублимации.

38. Ван-дер-Вальсом в ур-е Менделеева-Клапейрона (для идеального газа) внесены 2 поправки:

1.Учёт собственного объёма молекул.

Фактический свободный объём, в котором будут двигаться молекулы реального газа, будет не V_m, а V_m –b, где b – объём, занимаемый самими молекулами.

2.Учёт притяжения молекул.

Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. p’=a/ V²_m , где a – постоянная Ван-дер-Вальса, характеризующая силы межмолекулярного притяжения.

Уравнение Ван-дер-Вальса для моля газа (уравнение состояния реальных газов): (p+ a/ V²_m)( V_m –b)=RT

Для произвольного количества вещества ν газа (ν=m/M), с учётом того, что V=vV_m , уравнение Ван-дер-Валься примет вид

(p + v²a/V²)(V/v - b) = RT или (p + v²a/V²)(V - vb) = vRT

a и b – постоянные для каждого газа величины, определяемые опытным путём.

Изотермы Ван-дер-Вальса – кривые зависимоси p от V_m при заданных T, определяемые уравнением В-д-В для моля газа.

При высоких температурах (T>T_K) изотерма реального газа отличается от изотермы идеального очень мало. При некоторой температуре T_K на изотерме остаётся одна точка перегиба.

Эта изотерма наз. критической, а соотв. ей температура назыв. критической температурой. Критическая изотерма имеет лишь одну точку перегиба К, называемую критической точкой.

Соответствующие этой точке объём V_K и давление p_K называются критическими. Состояние с критическими параметрами называется критическим состоянием.

На участках 1-3 и 5-7 при уменьшении объёма давление растёт. На участке 3-5 сжатие вещества приводит к уменьшению давления; практика показывает, что такие сост-ния в природе не осуществ. Наличие участка 3-5 означает, что при постепенном изм. объёма вещ-во не может оставаться всё время в виде однородной среды; в некоторый момент должно наступить скачкообразное изм-е сост-я и распад вещества на две фазы. Т.о., истинная изотерма будет иметь вид ломаной линии 7-6-2-1. Часть 7-6 – газообр. сост., 2-1 – жидкое. 6-2 – равновесие жид. и газообр. фаз вещества.

Для нахожд-я критич. параметров подставим их знач-я в ур-е.

p_KV³ - (RT_K+p_Kb)V² + aV – ab = 0 (ур-е 3й степени относит-но V_m)

Поскольку в критической точке все 3 корня совпад. и равны V_K, ур-е приводится к виду p_K(V-V_K) ³=0 или

p_KV³ -3p_KV_KV² + 3p_KV²_KV- p_KV_K = 0

откуда p_KV³_K = ab, 3p_KV²_K = a, 3p_KV_K = RT_K + p_Kb

Решив их, получим: V_K = 3b, p_K = a/(27b²), T _K = 8a/(27Rb)

При некоторых условиях могут быть реализованы состояния, изображаемые на изотермах участками 5-6 и 2-3. Эти неустойчивые состояния наз. метастабильными. Участок 2-3 изобр. перегретую жидкость, 5-6 – пересыщенный пар. При достаточно низких температурах изотерма пересекает ось Vm, переходя в область отриц. давлений. Вещ-во под отриц. давлением нах. в сост. растяжения. Участок ниже точки 3 до p = 0 соотв. перегретой жидкости, участок убывания ниже оси Vm соотв. растянутой жидкости.

39. Внутр. энергия U реального газа равна сумме кинетической энергии W_k хаотического движения молекул и их взаимной потенциальной энергии W_п: U = W_k+ W_п. Внутр. энергия U_ид идеального газа предст-ет собой только кинетическую энергию хаотического движения молекул, поэтому: W_k= U_ид =∫C_vdT, где C_v- молярная теплоемкость газа в изохорном процессе. Пренебрегая зависимостью C_v от температуры, получаем W_k= C_vT. Таким обр., внутр. энергия моля реального газа U_m =C_vT+ W_п При адиабатном расширении газа без совершения полезной работы температура газа изменяется. Процесс такого необратимого расширения наз-ся адиабатным дросселированием, а явление изменения температуры в этом процессе – эффектом Джоуля – Томсона. Изменение внутр. энергии газа при прохождении через дроссель равно ∆U = Q+A’. Изменение температуры реального газа при адиабатном дросселировании равно ∆T= - (M∆W_п+∆(pV))/ mC_v.- интегральный эффект Джоуля-Томсона, наблюдаемый при конечном перепаде давления в дросселе. Для каждого газа в зависимости от его состояния перед –дросселем (p₁, T₁) и перепада давления в дросселе p₁-p₂ изменение температуры ∆T =T₂-T₁ может быть больше нуля – отрицательный эффект Джоуля-Томсона, меньше нуля – положит-й эффект и равно нулю – нулевой эффект Джоуля-Томсона.

40. Фазовый переход – превращение вещ-ва из одной фазы в другую при изменении внеш. условий. При фазовом переходе первого рода скачкообразно изменяются плотность, удельный и молярный объемы, концентрации компонентов, и выделяется или поглощается теплота (теплота фазового перехода). Н-р, переход вещ-ва из одного агрегатного состояние в другое, фазовые превращения твердых тел из одной кристаллической модификации в другую. При фазовом переходе второго рода теплота не поглощается и не выделяется, плотность измен-ся непрерывно, а скачкообразно измен-ся молярная теплоемкость, коэффициент теплового расширения, удельная элект-кая проводимость, вязкость и др. Примеры: переход нек-рых металлов и сплавов при низкой температуре из нормального состояния в сверхпроводящее.

КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ вещества, характеризуется наличием дальнего порядка в расположении частиц (атомов, ионов, молекул). В К. с. существует и ближний порядок, к-рый характеризуется постоянными координац. числами, валентными углами и длинами хим. связей. Инвариантность характеристик ближнего порядка в К. с. приводит к совпадению структурных ячеек при их трансляционном перемещении и образованию трехмерной периодичности структуры (см. Кристаллохимия. Кристаллы). Вследствие своей макс. упорядоченности К. с. в-ва характеризуется миним. внутр. энергией и является термодинамически равновесным состоянием при данных параметрах -давлении, т-ре, составе (в случае твердых растворов) и др. Строго говоря, полностью упорядоченное К. с. реально не м. б. осуществлено, приближение к нему имеет место при стремлении т-ры к О К (т. наз. идеальный кристалл). Реальные тела в К. с. всегда содержат нек-рое кол-во дефектов, нарушающих как ближний, так и дальний порядок. Особенно много дефектов наблюдается в твердых р-рах, в к-рых отдельные частицы и их группировки статистически занимают разл. положения в пространстве. Вследствие трехмерной периодичности атомного строения основными признаками кристаллов являются однородность и анизотропия св-в и симметрия, к-рая выражается, в частности, в том, что при определенных условиях образования кристаллы приобретают форму многогранников (см. Монокристаллов выращивание). Нек-рые св-ва в-ва на пов-сти кристалла и вблизи от нее существенно отличны от этих св-в внутри кристалла, в частности из-за нарушения симметрии. Состав и, соотв., св-ва меняются по объему кристалла из-за неизбежного изменения состава среды по мере роста кристалла. Т. обр., однородность св-в так же, как и наличие дальнего порядка, относится к характеристикам "идеального" К. с. Большинство тел в К. с. является поликристаллическими и представляет собой сростки большого числа мелких кристаллитов (зерен) - участков размером порядка 10^-1-10^-3 мм, неправильной формы и различно ориентированных. Зерна отделены друг от друга межкристаллитными слоями, в к-рых нарушен порядок расположения частиц. В межкристаллитных слоях происходит также концснтрирование примесей в процессе кристаллизации. Из-за случайной ориентации зерен поликристаллич. тело в целом (объем, содержащий достаточно много зерен) м. б. изотропным, напр. полученное при осаждении кристаллич. порошков с послед. спеканием. Однако обычно в процессе кристаллизации и особенно пластич. деформации возникает текстура - преимуществ, ориентация кристаллич. зерен в определенном направлении, приводящая к анизотропии св-в. На диаграмме состояния однокомпонентной системы вследствие полиморфизма К. с. может отвечать неск. полей, расположенных в области сравнительно низких т-р и повыш. давлений. Если имеется лишь одно поле К. с. и в-во химически не разлагается при повышении т-ры, то поле К. с. граничит с полями жидкости и газа по линиям плавления кристаллизации и возгонки - конденсации соотв., причем жидкость и газ (пар) могут находиться в метастабильном (переохлажденном) состоянии в поле К. с., тогда как К. с. не может находиться в поле жидкости или пара, т. е. кристаллич. в-во нельзя перегреть выше т-ры плавления или возгонки. Нек-рые в-ва (мезогены) при нагреве переходят в жидкокристаллич. состояние (см. Жидкие кристаллы). Если на диаграмме однокомпонентной системы имеются два и более полей К. с., эти поля граничат по линии полиморфных превращений. Кристаллич. в-во можно перегреть или переохладить ниже т-ры полиморфного превращения. В этом случае рассматриваемое К. с. в-ва может находиться в поле др. кристаллич. модификации и является метастабильным. В то время как жидкость и пар благодаря существованию критич. точки на линии испарения можно непрерывно перевести друг в друга, вопрос о возможности непрерывного взаимного превращ. К. с. и жидкости окончательно не решен. Для нек-рых в-в можно оценить критич. параметры -давление и т-ру, при к-рых H_пл и V_пл равны нулю, т. е. К. с. и жидкость термодинамически неразличимы. Но реально такое превращ. не наблюдалось ни для одного в-ва (см. Критическое состояние). В-во из К. с. можно перевести в неупорядоченное состояние (аморфное или стеклообразное), не отвечающее минимуму своб. энергии, не только изменением параметров состояния (давления, т-ры, состава), но и воздействием ионизирующего излучения или тонким измельчением. Критич. размер частиц, при к-ром уже не имеет смысла говорить о К. с., примерно 1 нм, т.е. того же порядка, что и размер элементарной ячейки. К. с. отличают обычно от др. разновидностей твердого состояния (стеклообразного, аморфного) по рентгенограммам в-ва

Дальний порядок и ближний порядок, упорядоченность во взаимном расположении атомов или молекул в твёрдых телах и жидкостях. Упорядоченность на расстояниях, сравнимых с межатомными, называется ближним порядком, а упорядоченность, повторяющаяся на неограниченно больших расстояниях, - дальним порядком. В идеальном газе расположение атома в какой-либо точке пространства не зависит от расположения других атомов. Т. о., в идеальном газе отсутствует Д. п. и б. п., но уже в жидкостях и аморфных телах существует ближний порядок - некоторая закономерность в расположении соседних атомов. На больших расстояниях порядок «размывается» и постепенно переходит в «беспорядок», т. е. дальнего порядка в жидкости и аморфных телах нет

Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами.

В зависимости от типов химической связи между узлами различают следующие типы решёток:

ионные,

атомные,

молекулярные,

металлические.

Закон Дюлонга-Пти (Закон постоянства теплоёмкости) — эмпирический закон, согласно которому молярная теплоёмкость твёрдых тел при комнатной температуре близка к 3R:

где R — универсальная газовая постоянная.

Закон выводится в предположении, что кристаллическая решетка тела состоит из атомов, каждый из которых совершает гармонические колебания в трех направлениях, определяемыми структурой решетки, причем колебания по различным направлениям абсолютно независимы друг от друга. При этом получается, что каждый атом представляет три осциллятора с энергией E, определяемой следующей формулой:

.

Формула вытекает из теоремы о равнораспределении энергии по степеням свободы. Так как каждый осциллятор имеет одну степень свободы, то его средняя кинетическая энергия равна , а так как колебания происходят гармонически, то средняя потенциальная энергия равна средней кинетической, а полная энергия - соответственно их сумме. Число осцилляторов в одном моле вещества составляет , их суммарная энергия численно равна теплоемкости тела - отсюда и вытекает закон Дюлонга-Пти.

41. В природе сущ-ет 2 рода эл-ких зарядов: «+»-ые и «-»-ые. Разноименно заряженные тела притягиваются, а одноименно заряженные отталкиваются друг от друга. Элек-ий заряд любой с-мы тел состоит из целого числа элементарных зарядов. Наименьшей по массе частицей, имеющей «-»-ный элементарный заряд является электрон. Наименьшая по массе устойчивая частица с «+»-ным элемент-ым зарядом – протон, представл-щий собой ядро атома наиболее распространенного в природе изотопа водорода. Электроны и протоны входят в состав всех атомов и молекул. Закон сохранения элект-го заряда: алгебраическая сумма элект-х зарядов тел или частиц, образующих элект-и изолированную с-му, не изменяются при любых процессах, происходящих в этой с-ме. Силы взаимодействия неподвижных элек-их зарядов подчиняются основному закону электростатического взаимодействия (закон Кулона) : сила электростатического взаимодействия двухточечных элек-их зарядов, наход-ся в вакууме, прямо пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между зарядами и направлена вдоль соединяющей их прямой:

F12 = k(q₁q₂/r²). Характерная особенность эл-кого поля, отличающая его от других физ-х полей, состоит в том, что оно действует на эл-ий заряд с силой, к-рая не зависит от скорости движения заряда. Колич-ной хар-кой силового действия эл-го поля на заряженные частицы и тела служит векторная величина Е - напряженность эл-кого поля. Е=отношению силы F, действующей со стороны поля на неподвижный точечный пробный эл-кий заряд, помещенный в рассматриваемую точку поля, к этому заряду q0. Напряженность электростатич. поля точечного заряда q в вакууме можно найти из закона Кулона: Е= (1/4πε₀)(q/r²). Энергетич-кой хар-кой поля служит его потенциал. Потенциал – физ-ая величина, равная отношению потенц-ой энергии пробного точечного эл-кого заряда, помещ-го в рассм-ую точку поля, к этому заряду q: φ=W/q. Потенциалы электростат. поля n точечных зарядов в вакууме = Σ(q_i / 4πε₀r_i )_. При наложении электростат. полей их потенциалы складываются алгебраически.

Электрическое поле — одна из составляющих электромагнитного поля, особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела. Электрическое поле материально.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы F действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

Также иногда называется силовой характеристикой электрического поля.

42. Сила, действ-щая со стороны электростат. поля на внесенный в него пробный точечный элек-ий заряд q, и потенциальная энергия этого заряда в поле равны: F=qE, W=qφ. С другой стороны, между потенциальной силой и потенц-ой энергией сущ-ет связь, выражаемая формулой: F= -gradW. Т.к. заряд q не зависит от координат точек поля, то: grad (qφ)=qgradφ. Поэтому между силовой хар-кой электростат. поля, напряженностью, и его энергетической хар-кой, потенциалом φ, сущ-ет след-ая связь: Е= - gradφ. Силовыми линиями наз-ся линии, проведенные в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряженности поля. Они не пересекаются, т.к. а каждой точке поля вектор имеет только одно определенное направление. Они начин-ся на «+»-ных зарядах и оканчиваются на «-»-ных. В случае поля двух одинаковых одноименных зарядов силовые линии искривлены. Эквипотенциальной пов-ю наз-ся геометрическое место точек электростат. поля, в которых значения потенциала одинаковы. Если вектор dr направлен по касательной к эквип. пов-ти, то эквипот. пов-ть ортогональа линииям напряженности. Работа, совершаемая силами электростатического поля при перемещении элект-го заряда по одной и той же эквипот. пов-ти, = 0. Вообще, есть 2 способа графич-го изображения электростат. полей – при помощи линий напряженности или эквипот. пов-ти. Направление силовой линии (линии напряженности) в каждой точке совпадает с направлением . Отсюда следует, что напряженность равна разности потенциалов U на единицу длины силовой линии.

      Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить наиболее просто:

      Теперь дадим определение эквипотенциальной поверхности. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности

      Графическое изображение силовых линий и эквипотенциальных поверхностей показано на рисунке 3.4.

Рис. 3.4

      При перемещении по этой поверхности на dl потенциал не изменится:

      Отсюда следует, что проекция вектора на dlравнанулю, то есть Следовательно, в каждой точке направлена по нормали к эквипотенциальной поверхности.

      Эквипотенциальных поверхностей можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине , это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине.

      Формула выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по известным значениям в каждой точке поля найти разность потенциаловмежду двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:

      С другой стороны работу можно представить в виде:

, тогда

      Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру получим:

      

      т.е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.

      Поле, обладающее этим свойством, называется потенциальным.

      Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут быть замкнутыми:они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность (рис. 3.4).

      Это соотношение верно только для электростатического поля. Впоследствии мы с вами выясним, что поле движущихся зарядов не является потенциальным, и для него это соотношение не выполняется.

43. Принцип суперпозиции элект-их полей: напряженность элект-го поля с-мы точечных зарядов равна сумме напряженностей полей каждого из этих зарядов в отдельности Е= ∑E_i, где Е – напряженность поля с-мы зарядов, а Е_i – напряженность поля одного заряда q_i. Е_i = (1/4πε₀)*(q/r_i³)* r_i; Е =(1/4πε₀)*Σ q_ir_i/ r_i³ . если заряды с-мы распределены в пространстве непрерывно, то напряженность поля этой с-мы в вакууме, согласно принципу суперпозиции полей, Е= 1/4πε₀∫dQr/r³, где r – радиус-вектор, проведенный в рассматриваемую точку поля из точки нахождения малого заряда dQ, а интегрирование проводится по всему заряду Q с-мы. Электр-ким диполем наз-ся с-ма состоящая из двух точечных электр-х зарядов равных по модулю, но противоположных по знаку заряда, расположенных на равном расстоянии. Произведение «+»-ного заряда q на плечо I наз-ся электр-ким моментом диполя: р_e = qI. Плечом диполя наз-ся вектор I, направленный по оси диполя от «-»-ного заряда к «+»-ному и по модулю равный расстоянию между ними.

44. Потоком напряженности эл-кого поля сквозь малый участок пов-ти, проведенной в поле, наз-ся величина dN=EdScos(E, m)=EdS, где Е –вектор напряженности эл-кого поля в точках малого участка пов-ти площадью dS; m- единичный вектор, нормальный к площадке dS, а вектор dS=dSn. Поток напряженности N сквозь любую пов-ть S= алгебраической сумме потоков напряженности сквозь все малые участки этой пов-ти. Теорема Остроградского–Гаусса для электростат. поля в вакууме: поток напряженности электростат. поля в вакууме сквозь произвольную замкнутую пов-ть равен отношению алгебраической суммы эл-ких зарядов, охватываемых этой пов-тью, к элект-ой постоянной ε₀. Φ EdS=q_охв/ε₀. Пов-ть S часто наз-ют гауссовой пов-тью. Справедливость теоремы Остроградского-Гаусса служит надежным подтверждением правильности закона Кулона.

45. Т.Остогр.-Гаусса: поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы электрических зарядов ,охватываемых этой поверхностью,к электрической постоянной ε₀ .