10. . Уравнения линии без потерь

Строго говоря, линий без потерь не существует. Однако в высокочастотных линиях, применяемых в радиотехнике, с достаточной степенью точности можно пренебречь продольным сопротивлением R₀ и поперечной проводимостью утечки G₀ по сравнению с индуктивным сопротивлением L₀ и емкостной проводимостью C₀, т.е. принять R₀ = G₀ = 0. В этом случае получается так называемая линия без потерь.

В такой линии волновое сопротивление

(13.39)

является чисто активным и не зависит от частоты.

Коэффициент распространения

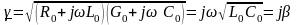(13.40)

является чисто мнимой величиной.

Коэффициент затухания  = 0, т.е. отсутствует затухание сигнала.

Фазовая скорость

(13.41)

постоянна и равна скорости света.

Уравнения линии через параметры нагрузки (13.20) для линии без потерь запишутся:

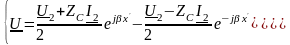(13.42)

Тогда гиперболические уравнения линии (13.21) в линии без потерь переходят в уравнения с тригонометрическими функциями от действительного аргумента

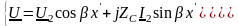. (13.43)

Входное сопротивление линии

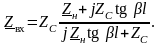
11.Режим согласованной нагрузки (Z_н = Z, ). Подставляя эти выражения в соотношения для напряжения и тока, получим:

Отсюда следует, что при согласованной нагрузке напряжение и ток в линии без потерь имеют постоянную амплитуду по всей длине. Входное сопротивление Z_вх такой линии равно ее волновому сопротивлению Z, и не зависит от длины линии.

12.коэф-т бегущей волны: K_бв = (1 - n) / (1 + n)

13. Режим холостого хода ( ). Для комплексных напряжений и тока имеем:

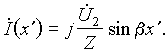
В рассматриваемом режиме напряжение и ток во всех точках линии имеют одинаковую фазу. Действительно, для мгновенного значения напряжения при холостом ходе получим . Согласно этому соотношению, напряжение во всей линии изменяется синфазно. Эти колебания представляют собой так называемые стоячие волны. На рис. 25.4 изображено распределение действующих токов и напряжений для случая, когда l = 2, т. е. длина линии l равна длине волны 

Рис. 25.4

Поскольку в отдельных точках линии, как следует из рисунка, напряжение сохраняет нулевое значение, то по линии в целом отсутствует передача мощности.

Входное сопротивление разомкнутой на конце линии Z_вх = – jZ ctg l имеет место чисто реактивный характер (волновое сопротивление Z линии без потерь — вещественная величина). В зависимости от длины линии входное сопротивление может иметь как емкостный (например, при 0 < l < /2), так и индуктивный характер (/2 < l < ). Если длина разомкнутой на конце линии l равна четверти длины волны (l = /2), то ее входное сопротивление равно нулю.

14. Режим короткого замыкания ( ). Распределение комплексных напряжения и тока выражается формулами:

И в этом случае в линии наблюдаются стоячие волны, однако теперь узел напряжения расположен в конце линии (рис. 25.5), а распределение тока в этой точке имеет пучность.

Рис. 25.5

Как и при холостом ходе, передача энергии по линии в целом в этом режиме отсутствует. Для входного сопротивления из общей формулы получим Z_вх =jZ tg l. Оно также имеет чисто реактивный характер и в зависимости от длины линии может быть индуктивным или емкостным.

Сопоставляя оба рассмотренных режима (х. х. и к. з.), можно заключить, что соотношение между входными сопротивлениями в обоих режимах существенно зависит от волновой длины линии l/ = l/2. При l/ <1/8 (l < /4) имеем Z_{вх. к.з.} <  Z_{вх. х.х.}, однако при /4 < l < /2 это неравенство изменяется на обратное; для четвертьволновой линии (l = /2) Z_{вх. х.х.} = 0, а Z_{вх. к.з.} = . Этот парадоксальный результат объясняется тем, что при холостом ходе в начале линии имеем узел напряжения, а при коротком замыкании — узел тока.

15. При нагрузке линии на емкость или индуктивность с реактивным сопротивлением X_н выходные величины связаны соотношением U₂ = jX_н I₂. Его подстановка в соотношения для напряжения и тока позволяет записать их в виде:

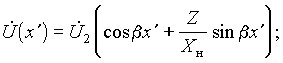
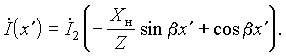
Поскольку реактивное сопротивление нагрузки X_н вещественно, то отсюда вытекает, что и при нагрузке линии без потерь на емкость или индуктивность фаза напряжения и тока во всех точках линии одинакова. Таким образом, и в этом режиме в линии наблюдаются стоячие волны тока и напряжения. 

Для более ясного представления о характере распределения преобразуем полученные выражения, используя представление параметра Z/X_н = tgЭлементарные тригонометрические преобразования позволяют привести рассматриваемые формулы к виду . Эти выражения показывают, что, как и в рассмотренных выше случаях, распределение действующих токов и напряжений имеет синусоидальный характер (см. рис. 25.4), однако в отличие от режимов холостого хода и короткого замыкания в конце линии нет ни узла, ни пучности. Положение узлов и пучностей легко определяется из последних выражений.