
Функціі багатьох змінних
Припустимо,
що на площині чи у просторі фіксована
система декартових координат. Через
ρ(x,y)
позначається відстань між точками і у
випадку площини:
![]()
У
випадку простору:
![]()
Зауважимо, що відстань між точками x і y має властивості:
1) ρ(x,y)=ρ(y,x)
2) ρ(x,y)≤ρ(x,z)+ρ(z,y)
Нехай ми маємо сукупність дійсних чисел x(x1,x2,…,xn) – точка n-мірного простору, позначають як x. Аналогічно y(y1,y2,…,yn). n-мірний простір називають евклідовим, якщо відстань між його двома довільними точками знаходять як
![]()
n=1 – пряма R1.
n=2 – площина R2.
n=3 – простір R3.
Нехай Е c Rn (множина точок n-мірного простору). x0(x01,x02,…,x0n) є Е – внутрішня точка цієї множини, якщо існує окіл цієї точки, що цілком належить даній множині.
Точка x0 називається граничною, якщо в довільному околі є точки, відмінні від x0.
Множина Е – відкрита, якщо кожна ії точка є внутрішньою.
Множина Е – замкнена, якщо вона містить в собі всі свої граничні точки.
Числові послідовності в n-мірному просторі
Нехай
Е – деяка можина простору Rn.
Числовою послідовністю n-мірного
простору називають закон чи правило,
за яким кожному натуральному k
ставиться у відповідність точка
xk(xk1,xk2,…,xkn).
Позначають
як {xk}.
xk
– загальний
член послідовності. Число A
– границя
послідовності xk,k→∞,
якщо
![]()
![]()
Поняття функціі багатьох змінних
Припустимо, що в n-мірному просторі задана E c Rn.
Функцією називають закон/правило, за яким кожній точці множини Е ставиться число U=f(x1,x2,…,xn). x1..xn – незалежні змінні(аргументи).
При n=1 U=f(x);
n=2 U=f(x,y);
n=3 U=f(x,y,z);
Графік ф-ціі однієі змінної – лінія.
Границя функцій багатьох змінних
Нехай f(x)=f(x1,x2,…,xn) Е с Rn. x0(x01,x02,…,x0n) – гранична точка Е.
1. Означення границі ф-ціі на мові «εδ».

2. Означення границі на мові послідовностей
![]() Ці
два означення еквівалентні.
Ці
два означення еквівалентні.
Неперервність функціі в точці
Нехай f(x)=f(x1,x2,…,xn) x є E c Rn x0(x01,…,x0n)
1) Означення неперервності на мові границь
![]()
2) Означення неперервності на мові «ε-δ»
![]()
3) Означення неперервності на мові приростів
Нехай x0(x01,x02,…,x0n) є Е. Надаємо кожній змінній x01..x0n приростів (x01+Δx1..x0n+Δxn) є Е. f(x01..x0i-1,x0i+Δxi,x0i+1..x0n)-f(x01..x0n)=Δxif(x0) – частковий приріст по xi.
![]()
Повний приріст f(x) в т. x0 називається Δf(x0)=f(x01+Δx1..x0n+Δxn)-f(x01..x0n).
Функція
називається неперервною в x0
по
сукупності змінних x1..xn,
якщо границя повного приросту

Тобто нескінченно малим приростам аргументів відповідає нескінченно малий повний приріст в даній точці. Функція f(x) неперервна на множ. Е, якщо вона неперервна в кожній точці цієі множ.
Частинні похідні ф-ціі багатьох змінних

Частинна
похідна в т. x0
по змінній xi
– скінченна границя
відношення частинного приросту по Δxi:
Тобто частинна похідна – звичайна похідна по одній із змінних при фіксованих інших змінних.
Диференційовність ф-ціі багатьох змінних в точці
F(x)=f(x1..xn) E c Rn x0(x01..x0n) є E
Ф-ція
f(x) диференційовна в т. x0,
якщо
 (1)
(1)
Перший
доданок правої частини рівності (1) є
лінійною ф-цією відносно приростів
аргументів Δx1..Δxn.
Оскільки Ai
– константи при i=1..n, то другий доданок
– нескінченно мала ф-ція порядку вищого,
ніж перший доданок правої частини
рівності (1). Головна відносно Δx1..Δxn
частина
повного приросту f(x) називається повним
диференціалом f(x) в т. x0
і позначається df(x0).
Тоді
за означенням повного диференціалу![]()
Необхідні умови диференційовності ф-ціі в точці
1. Теорема 1: якщо f(x) є D(x0), то f(x) є C(x0).
Доведення:

2.
Теорема 2: якщо f(x) є D(x0),
то
![]()
Доведення:
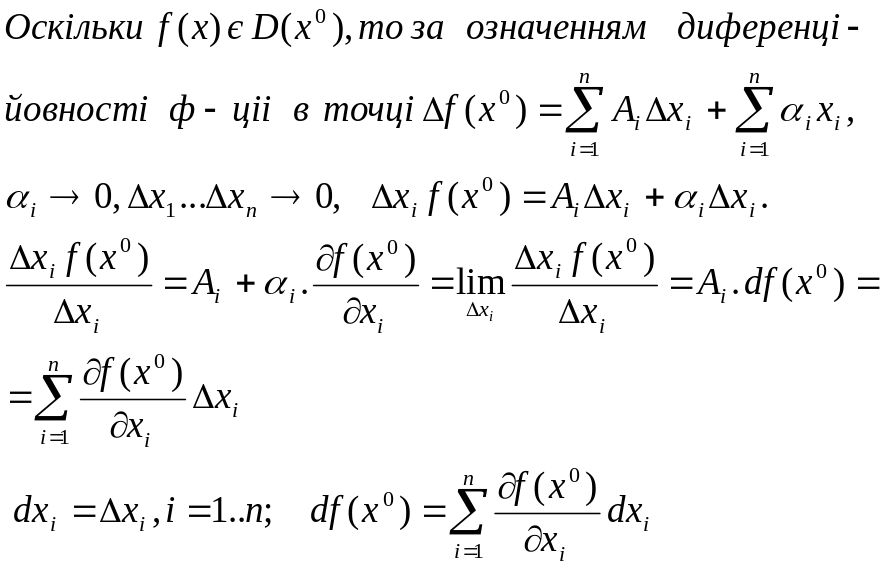
Достатня умова диференційовності ф-ціі в точці
Якщо
f(x)=f(x1..xn)
![]() ,
f(x) є D(x0).
,
f(x) є D(x0).
Доведення: проведемо для ф-ціі двох змінних.

Геометр інтерприт повного диференц ф-ції в точці
Z=f(x,y) E нал. R2. Графіком є деяка пов z=x2+y2
Площ z-z0=A(x-x0)+B(y-y0) –дотична до поверхні
Z=f(x,y) (x0, y0, f(x0, y0) ), якщо z-f(x,y) прямує до 0.
Прип, що f(x,y) диф. на (x0, y0), тоді

Рів-ня 2). – рів-ня дотичної площини. Повний диференціал ф-ції двох змінних дорівнює приросту аплікати дотичної площ, проведеної до графіку поверхні z=f(x,y) в т. (x0,y0,z0).
Диференційовність ф-ції багатьох змінних
Припустимо,
що ф-ція
![]()

Похідна ф-ціі по заданному напрямку
Припустимо, що у просторі задана область v, в кожній точці якої f(x,y,z). В області v задана пряма l, що має напрямок. Нехай cosα, cosβ, cosγ – напрямні косинуси прямої l. Нехай т. M0 належить прямій l, а т. M(x,y,z) – зовнішня точка. Побудуємо вектор M0M, Δа=|M0M|

![]()
Частинні похідні вищих порядків
Припустимо, що f(x)=f(x1..xn) є D(x0), x0(x01..x0n).
Значить, в даній точці існують частинні похідні по кожній зі змінних.

Диференціали вищих порядків

Формула Тейлора для ф-цій багатьох змінних
Якщо
f(x1...xn)
є D(X),
x0(x01..x0n),
то

Екстремум ф-ціі багатьох змінних

Необхідна умова існування екстремуму ф-ціі багатьох змінних

Доведення

Достатня умова існування екстремуму

Достатня умова існування екстремуму ф-ціі двох змінних

Задача про обчислення об’єму циліндричного бруса

Поняття подвійного інтегралу
 Умови
існування подвійного інтегралу
Умови
існування подвійного інтегралу
Необхідна умова
![]()
Достатня умова
![]()
Властивості подвійного інтегралу
