1. Находим оптимальные стратегии второго игрока по матрице

					0			12			1
					11			9			1
					-1			-1			0

	0	12	1
	1/11	9/11	1/11
	1/11	-2/11	1/11

	0	1/12	1/12
	1/11	-9/(11∙12)	3/(11∙12)
	1/11	2/(11∙12)	14/(11∙12)

,

- Оптимальная стратегия второго игрока b.

2. Для матрицы b решаем соответствующую пару двойственных задач линейного программирования:

, выбрав с=2, получим

	7	0	1
	1/3	1/3	1/3
	-2/3	1/3	1/3

	7	0	1
	1	3	1
	-1	-1	0

			1/7
			2/7
	2/(21)	1/3	3/(7)

Из последней таблицы получим:

, ;

Тогда оптимальная стратегия будет:

; и

- оптимальная стратегия первого игрока A.

После получения оптимальных стратегий игроков А и В найдём м.о. выигрышей этих игроков

;

;

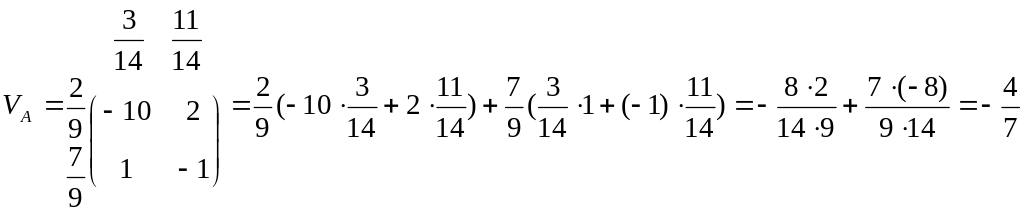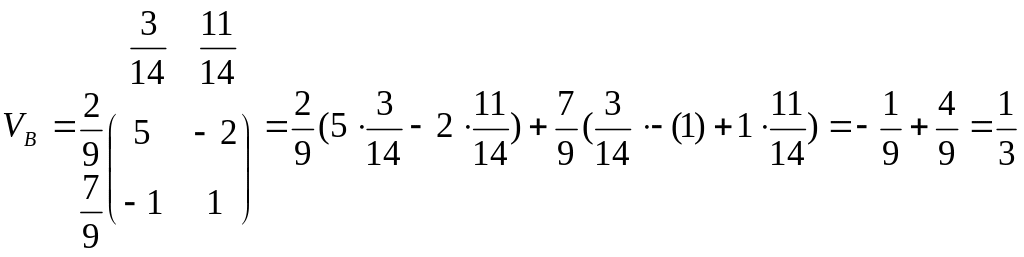Биматричную игру или можно решить графически.