18.2.6. Разложение в ряд Маклорена элементарных функций.
18.2.6.1. Стандартные разложения.
.
Всё начинается с
геометрической прогрессии. На первой
лекции по рядам (см. раздел 18.1.
Основные определения)
мы доказали, что эта функция является
суммой ряда
,
и ряд сходится к функции при
.
Итак,
.
Выпишем несколько разновидностей этого ряда. Заменив х на -х, получим
;
при замене х
на 
получаем
;
;
и т.д.; область
сходимости всех этих рядов одна и та
же:
.
2.
.
Все производные
этой функции в точке х=0
равны 
,
поэтому ряд имеет вид
.
Область сходимости
этого ряда - вся числовая ось (пример 6
раздела 18.2.4.3.
Радиус сходимости, интервал сходимости
и область сходимости степенного ряда),
поэтому 
при 
.
Как следствие, остаточный член формулы
Тейлора 
.
Поэтому ряд сходится к
в любой точке
х.
3.
.
Здесь 
дальше производные
периодически повторяются. Ряд Маклорена
имеет вид
.
Этот ряд абсолютно
сходится при 
,
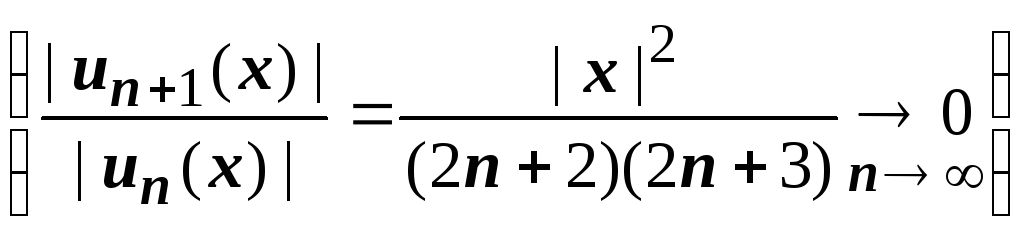и его сумма действительно равна 
.
Остаточный член формулы Тейлора имеет
вид 
,
где 
или 
- ограниченная функция, а 
(это общий член предыдущего разложения).
4.
.
Это разложение можно получить, как и предыдущие, последовательным вычислением производных, но мы поступим по другому. Почленно продифференцируем предыдущий ряд:
.
Сходимость к функции на всей оси следует из теоремы о почленном дифференцировании степенного ряда.
5. Самостоятельно
доказать, что на всей числовой оси 
,
.
6.
.
Ряд для этой функции называется биномиальным рядом. Здесь мы будем вычислять производные.
…Ряд Маклорена
имеет вид
Ищем интервал
сходимости: 
, следовательно, интервал сходимости
есть 
.
Исследование остаточного члена и
поведение ряда на концах интервала
сходимости проводить не будем; оказывается,
что при 
ряд абсолютно сходится в обеих точках
,
при 
ряд условно сходится в точке 
и расходится в точке 
,
при 
расходится в обеих точках.
7.
.
Здесь мы воспользуемся
тем, что
.
Так как 
,
то, после почленного интегрирования,
.
Область сходимости
этого ряда - полуинтервал 
,
сходимость к функции во внутренних
точках следует из теоремы о почленном
интегрировании степенного ряда, в точке
х=1
- из непрерывности и функции, и суммы
степенного ряда во всех точках, сколь
угодно близких к х=1
слева. Отметим, что взяв х=1,
мы найдём сумму ряда 
.
8. Почленно
интегрируя ряд 
,
получим разложение для функции 
.
Выполнить все выкладки самостоятельно,
выписать область сходимости.
9.
Выпишем
разложение функции 
по формуле биномиального ряда с 
:
.
Знаменатель 
представлен как 
,
двойной факториал 
означает произведение всех натуральных
чисел той же чётности, что и 
,
не превосходящих 
.
Разложение сходится к функции при
.
Почленно интегрируя его от 0 до х,
получим 
.
Оказывается, что этот ряд сходится к
функции на всём отрезке
;
при х=1
получаем ещё одно красивое представление
числа
:
.
18.2.6.2. Решение
задач на разложение функций в ряд.
Большинство
задач, в которых требуется разложить
элементарную функцию в ряд по степеням
,
решается применением стандартных
разложений. К счастью, любая основная
элементарная функция имеет свойство,
которое позволяет это сделать. Рассмотрим
ряд примеров.
1. Разложить функцию
по степеням 
.
Решение.
.
Ряд сходится при 
.
2. Разложить функцию
по степеням 
.
Решение.
.
Область сходимости: 
.
3. Разложить функцию
по степеням 
.
Решение.
.
Ряд сходится при 
.
4. Разложить функцию
по степеням 
.
Решение.
.
Ряд сходится при 
.
5. Разложить функцию
по степеням 
.
Решение.
.
Область сходимости 
.
6. Разложить функцию
по степеням 
.
Решение.
Разложение в ряд простых рациональных
дробей второго типа получается почленным
дифференцированием соответствующих
разложений дробей первого типа. В этом
примере 
.
Дальше почленным дифференцированием
можно получить разложения функций 
,
и т.д.
7. Разложить функцию
по степеням 
.
Решение.
Если рациональная дробь не является
простой, она сначала представляется в
виде суммы простых дробей: 
,
а затем действуем, как в примере 5: 
,
где
.
Естественно, такой
подход неприменим, например, для
разложения функции 
по степеням х.
Здесь, если надо получить несколько
первых членов ряда Тейлора, проще всего
найти значения в точке х=0
требуемого количества первых производных.