6.3. Пересечение гранных поверхностей с поверхностями вращения

При пересечении поверхности вращения многогранником их общим геометрическим элементом является некоторая линия.

Рассмотрим построение этой линии на примере решения задачи о пересечении прямой трехгранной призмы и сферы (рис. 6.3).

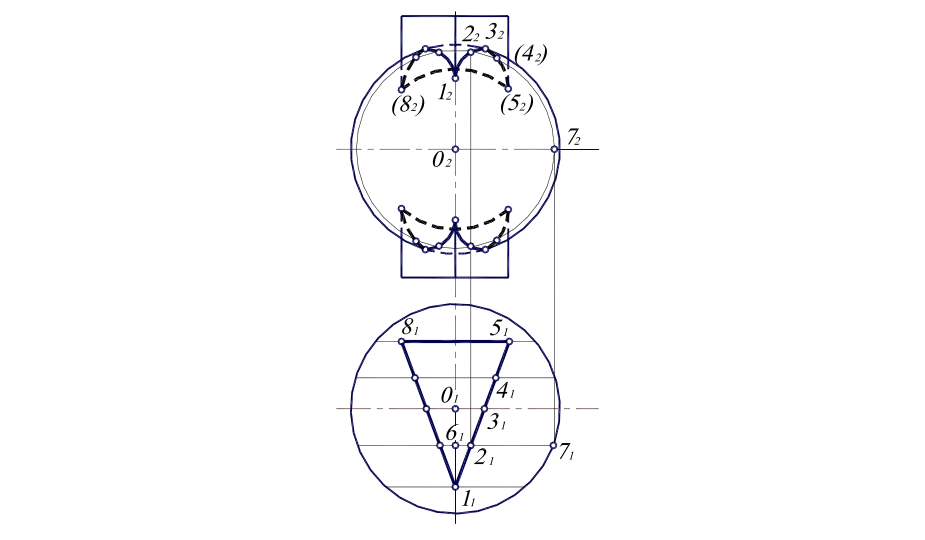
Рис. 6.3. Пересечение призмы и сферы.

Поскольку боковые грани призмы перпендикулярны к П₁, то горизонтальная проекция линии пересечения призмы и сферы совпадает с горизонтальной проекцией боковой поверхности призмы.

Остается построить фронтальную проекцию линии пересечения. Так как по двум проекциям геометрического объекта легко построить третью, то здесь мы ограничимся построением горизонтальной и фронтальной проекций.

В данном случае, поскольку одна из поверхностей занимает частное положение в пространстве, то применения метода вспомогательных секущих плоскостей не требуется. Выберем характерные (1, 3, 5) и промежуточные (2, 4) точки, лежащие на линии пересечения призмы и сферы. Их горизонтальные проекции 1₁, 2₁, 3₁, 4₁, 5₁ указаны на рис. 6.3.

Для построения на П₂ проекции какой-либо из указанных точек достаточно через горизонтальную проекцию искомой точки провести горизонтальную линию, фронтальная проекция которой представляет собой окружность, далее измерить расстояние вдоль этой линии от вертикальной оси до контура сферы на П_1, а затем этим радиусом на П₂ провести окружность.

Рассмотрим построение фронтальной проекции какой-либо точки, например, точки 2. Проводим через нее горизонтальную линию. Затем измеряем расстояние от точки 6₁ до 7₁ и этим радиусом проводим дугу окружности из точки О₂. Искомая точка 2₂ лежит на пересечении дуги окружности с линией связи, проведенной из точки 2₁. Аналогично строятся точки 1₂, 4₂, 5₂. Через точку 3 нет необходимости проводить горизонтальную линию, так как она лежит на контуре сферы в проекции на П₂, и для построения точки 3₂ достаточно провести из точки 3₁ линию связи до пересечения ее с контуром сферы.

Соединив точки 1₂, 2₂, 3₂, 4₂, 5₂, получаем один из участков искомой линии.

Так как участок линии между точками 5₁ и 8₁ лежит на горизонтальной линии, то между точками 5 и 8 линия пересечения призмы и сферы представляет собой дугу окружности.

В связи с тем, что рассматриваемые поверхности симметричны относительно горизонтальной и профильной плоскостей уровня, искомая линия пересечения в проекции на П₂ симметрична относительно вертикальной и горизонтальной осей, и ее построение не требует дополнительных пояснений.

Видимость линий определяется по видимости точек так же, как в предыдущих разделах.

Заметим, что, используя метод вспомогательных секущих плоскостей, можно построить линию пересечения любых геометрических объектов (прямой с плоскостью, многогранником, поверхностью вращения, двух плоскостей, плоскости общего положения с многогранником и поверхностью вращения и т.п.). Если при построении линий пересечения вспомогательных секущих плоскостей и рассматриваемых поверхностей возникают затруднения, тогда необходимо способом замены плоскостей проекций получить проекции указанных поверхностей в более удобном виде.