Вычисление криволинейного интеграла второго рода.

.

Пусть . Запишем.

Тогда криволинейный интеграл второго рода можно записать в виде

.

Параметризуем дугу L = AB:,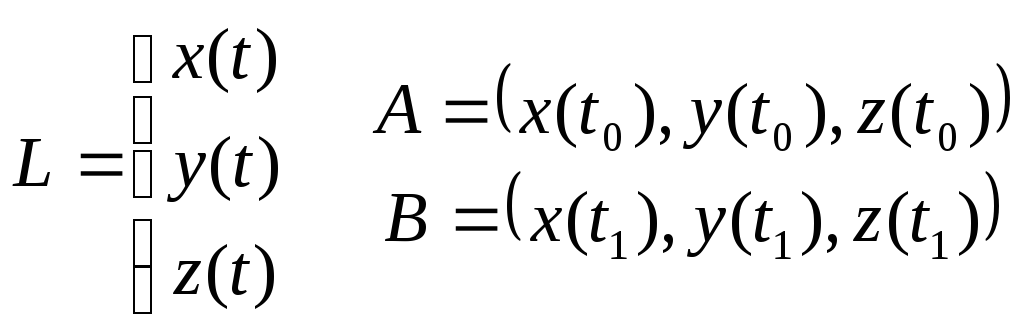

непрерывны, так как дуга гладкая. Подставим эти выражения в криволинейный интеграл, он превратится в определенный интеграл по параметру.

=.

Пример.Вычислить, где- один виток винтовой линии,.

=.

Пример. Вычислить интегралпо трем различным дугам, соединяющим точкиA(0,0,), B(1,1,) - ломаная, соединяющая точкиA, C(1,0), B,

1. ,

2. 

3. 

Пример. Показать, чтопо всем указанным выше дугам.

Лекция 6. Формула Грина.

Теорема (формула) Грина.ПустьG– плоская односвязная область с кусочно-гладкой границейL. Пусть функцииP(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные по своим переменным в областиGи наL.

Тогда справедлива формула Грина

.

Доказательство.1) Назовем плоскую областьD(в плоскостиOXY) правильной, если любая прямая, параллельная координатной оси(OX илиOY) пересекает область не более, чем в двух точках. Можно показать, что областьG можно представить как объединение конечного числа правильных областей .

Тогда по свойству аддитивности двойной интеграл в правой части формулы Грина равен сумме двойных интегралов по правильным областям. Криволинейный интеграл в левой части равен сумме криволинейных интегралов по границам правильных областей, так как криволинейные интегралы по общим границам любых правильных областей различны по знаку из-за различных направлений обхода границы и взаимно уничтожаются при суммировании.

Поэтому доказательство может быть проведено для правильной области G.

2) Пусть G– правильная область. Так какP, Qмогут быть произвольными функциями, то формула Грина сводится двум формулами, каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.

= == =

Вычисление площади области по формуле Грина.

По свойству 3 двойного интеграла площадь области Dможно вычислить по формуле

. Поэтому достаточно выбратьP, Qтак, чтобы, чтобы с помощью криволинейного интеграла по формуле Грина можно было бы вычислять площадь области.

Например, можно выбрать Q=x, P=0. Тогда . Можно выбратьQ=0, P=y, тогда. Очень полезна бывает симметричная формула при.

Пример. Вычислить площадь эллипса с полуосямиa, b

.

Полный дифференциал и его вычисление.

Теорема (о полном дифференциале). Для того чтобы выражение- было полным дифференциалом некоторой функции- потенциала, необходимо и достаточно, чтобы в условиях формулы Грина было выполнено одно из следующих четырех условий (эквивалентных условий полного дифференциала)

1. зависит только от начальнойA и конечнойBточек дуги и не зависит от формы дуги (не зависит от пути интегрирования),

2. для любого кусочно-гладкого контура

3. ,

4. .

Доказательство.Схема доказательства теоремы. По этой цепочке можно последовательно добраться от любого пункта к любому другому.

Дополнительно предположим, что существуют и непрерывны вторые смешанные производные функцииV. Тогда они равны.

.

. Это следует из формулы Грина.

. Пусть точкиA, Bсоединены двумя дугамиL₁ и L₂. Тогда из них можно составить контур , интеграл вдоль которого по п.2 равен нулю.

== -

. Поэтому =.

. Докажем, что- потенциал, то есть, что

. Докажем первое соотношение, второе доказывается аналогично.

=

Заметим, что такая запись интеграла показывает, что интеграл не зависит от формы дуги. Поэтому мы можем в первом интеграле провести дугу через точку (x, y), чтобы в первом и втором интеграле сократились интегралы по дуге, соединяющей начальную точку с точкой(x, y). В первом интеграле выберем в качестве дуги, соединяющей точку (x, y) с точкой (x+x) отрезок прямой, параллельный осиOX. На этом отрезкеyне изменяется, поэтомуdy=0

Тогда, продолжая равенство, получим

= =

(здесь мы перешли от криволинейного интеграла к определенному, так как дуга интегрирования – отрезок, параллельный оси OX и применили теорему о среднем для определенного интеграла). Теперь используем непрерывность функцииP(x, y) по переменнойx.

= . Первое соотношение доказано.

Для доказательства второго соотношения варьируется переменная y, дуга, соединяющая точки (x_0, y₀), и (x, y+y) проводится через точку(x, y) и далее по отрезку, параллельному осиOY, соединяющему точки(x, y) и (x, y+y).