Лекция 3 Тройной интеграл. Задача о массе пространственного тела.

Пусть есть некоторое пространственное материальное тело, занимающее область V, в каждой точке которой задана объемная плотностьf(x,y, z). Надо вычислить массу пространственного тела.

Эта задача приводит к понятию тройного интеграла.

Введем разбиение области Vна элементарные области, не имеющие общих внутренних точек (условие А) v_k с малым объемом(обозначение области и ее объема обычно одно и то же, это принято уже более 200 лет и не вносит путаницы).

На каждом элементе разбиения – элементарной области отметим точку M_k(x_k, y_k, z_k). Вычислим плотность в этой точкеf(x_k, y_k, z_k) = f(M_k) и предположим, что плотность постоянна в элементарной области. Тогда масса элементарной областиv_k приближенно равна=f(M_k) . Суммируя все такие массы элементарных областей (составляяинтегральную сумму), приближенно получим массу областиV

Для того, чтобы точно вычислить массу области, остается перейти к пределу при условии (условие B).

.

Так задача о массе пространственной области приводит к тройному интегралу⁷.

Введем некоторые ограничения на область интегрирования и подинтегральную функцию, достаточные для существования интеграла⁸.

Потребуем, чтобы функция f(M) была непрерывна в области V и на ее границе.

Потребуем, чтобы область V была замкнутой, ограниченной, пространственно-односвязной областью с кусочно-гладкой границей.

Область назовем пространственно-односвязной, если ее можно непрерывной деформацией стянуть в точку.

Теорема существования. Пусть областьVи функцияf(M)=f(x, y, z) удовлетворяют сформулированным требованиям. Тогда тройной интеграл существует как предел интегральных сумм.

.

Замечание.Предел этот не зависит⁹:

1) от выбора разбиения области, лишь бы выполнялось условие А

2) от выбора отмеченных точек на элементах разбиения

3) от способа измельчения разбиения, лишь бы выполнялось условие B.

Свойства тройного интеграла.

1. Линейность а) =+

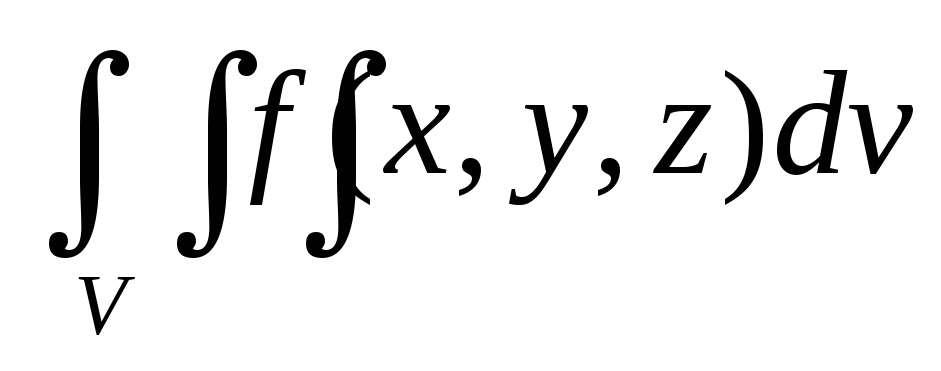б) =Эти свойства, как и для двойного интеграла, доказываются «через интегральные суммы». Составляют интегральную сумму для интегралов, стоящих в левой части равенства, в ней делают нужную операцию (это возможно, т.к. число слагаемых конечно) и получают интегральные суммы для интегралов в правой части. Затем, по теореме о предельном переходе в равенстве, переходят к пределу, и свойство доказано.

2. Аддитивность (по множеству) =+

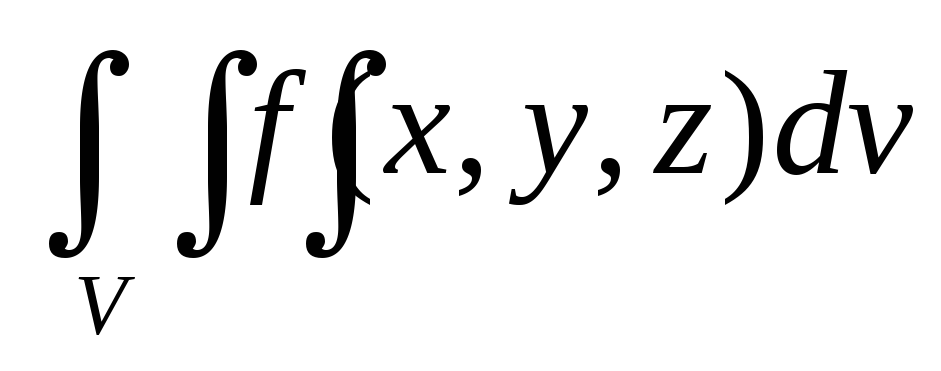Доказательство проводится, как и ранее, через интегральные суммы с использованием замечания к теореме существования.

Разбиение выбирается и измельчается так, чтобы граница областей V, Wсостояла из границ элементов разбиения (это можно сделать, учитывая замечание). Тогда интегральная сумма для интеграла в левой части равенства равна сумме двух интегральных сумм, каждая для своего для интеграла в правой части равенства. Переходя к пределу в равенстве, получаем требуемое соотношение.

3. , где– объем областиV. Интегральная сумма для интеграла в левой части=

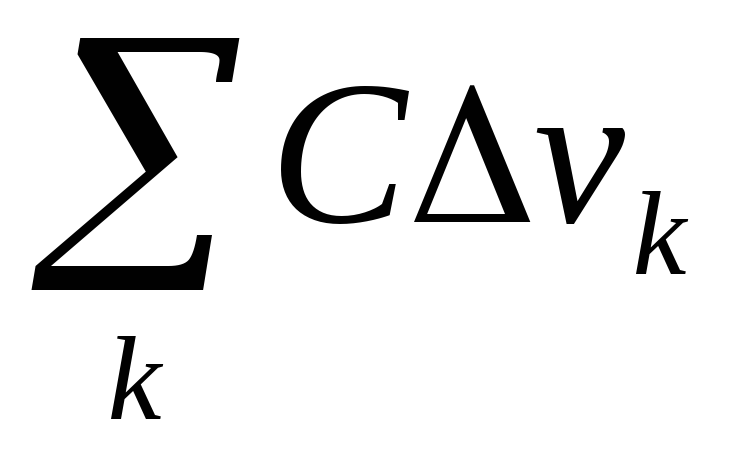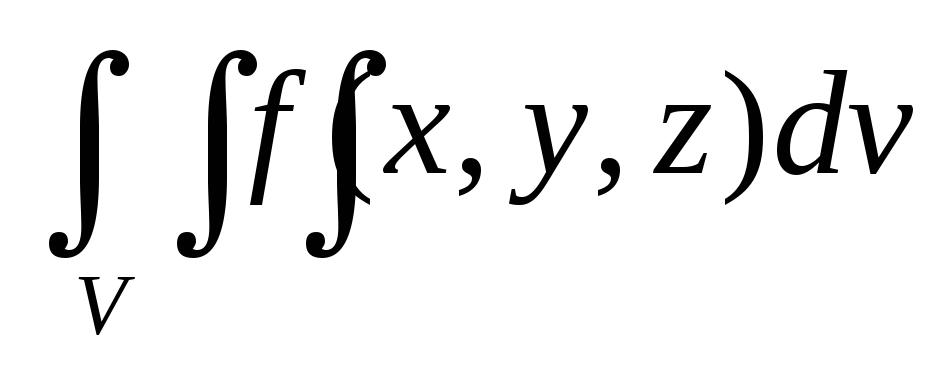
4. Если f(x, y, z) g(x, y, z), то. Переходя к пределу в неравенстве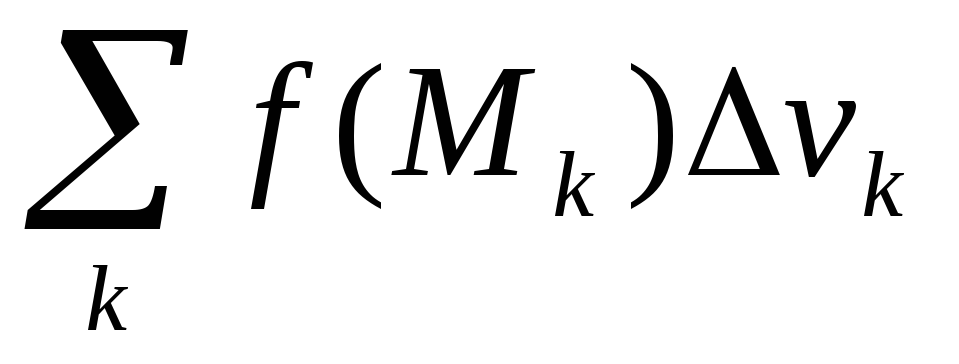(по теореме о переходе к пределу в неравенстве), получим требуемое соотношение.Следствие. Еслиf(x, y, z) 0, то 0.

5. Теорема об оценке интеграла. Еслиmf(x, y, z) M, тоmVMV. Интегрируя неравенствоmf(x, y, z) M, по свойству 4 получим требуемое неравенство.

6. Теорема о среднем. Пусть выполнены требования теоремы существования. Тогда Существует точка С в областиV, такая, чтоf(C) = .

Доказательство. Так как функция непрерывна на замкнутом ограниченном множествеV, то существует ее нижняя граньи верхняя грань. Выполнено неравенство. Деля обе части наполучим. Но числозаключено между нижней и верхней гранью функции. Так как функциянепрерывна на замкнутом ограниченном множестве, то в некоторой точкефункция должна принимать это значение. Следовательно, f(C) = .