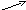Примеры:
1.
![]() .
.
I.
 ;
общего вида; непериодична;
;
общего вида; непериодична;
![]() при
при
![]() ;
;
![]()

![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
точка
;
точка
![]() - точка разрыва второго рода; прямая
- точка разрыва второго рода; прямая
![]() - вертикальная асимптота. Ищем наклонные
асимптоты:
- вертикальная асимптота. Ищем наклонные
асимптоты:
![]() ;
;
![]() ;
прямая
;
прямая
![]() - двусторонняя наклонная асимптота.
Интервалы знакопостоянства функции:
- двусторонняя наклонная асимптота.
Интервалы знакопостоянства функции:
II.
![]()
![]() .
Критические точки первого рода:
.
Критические точки первого рода:
![]() ,
,
![]() .
Определяем интервалы монотонности (в
таблицу включаем концы интервалов
области определения и критические
точки):
.
Определяем интервалы монотонности (в
таблицу включаем концы интервалов
области определения и критические
точки):
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
|
|
|
0 |
+ |
|
|
|
Мax=0 |
|
Не опред. |
|
Min= |
|
III.
![]()
![]()
Критические точки
второго рода:
![]() ,
,
![]() .
Определяем интервалы выпуклости графика:
.
Определяем интервалы выпуклости графика:
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
|
0 |
|
|
+ |
|
|
|
Точка перегиба |
|
Нет перегиба |
|
Не опред. |
|
Г рафик
функции приведён на рисунке справа.
рафик
функции приведён на рисунке справа.
2.
![]() .
.
I.
 ;
общего вида; непериодична.
;
общего вида; непериодична.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Точка
.
Точка
![]() -
точка разрыва второго рода; прямая
-
точка разрыва второго рода; прямая
![]() - вертикальная асимптота. Так как функция
не определена при
- вертикальная асимптота. Так как функция
не определена при
![]() ,
ищем только правую наклонную асимптоту:
,
ищем только правую наклонную асимптоту:
![]() ,
,
![]() ,
наклонной асимптоты нет. Функция
принимает отрицательные значения на
интервале
,
наклонной асимптоты нет. Функция
принимает отрицательные значения на
интервале
![]() ,
положительные значения на интервале
,
положительные значения на интервале
![]() .
.
II.
![]() ,
единственная стационарная точка -
,
единственная стационарная точка -
![]() .
Интервалы монотонности:
.
Интервалы монотонности:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
+ |
|
|
|
Не опред. |
|
Min= |
|
III.
![]() ,
,
![]() -
критическая точка второго рода. Интервалы
выпуклости:
-
критическая точка второго рода. Интервалы
выпуклости:
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
|
|
|
|
Не опред. |
|
Точка перегиба |
|
Г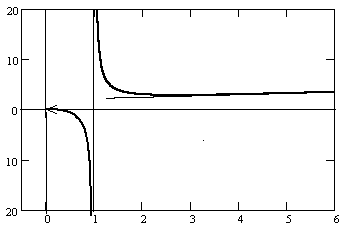 рафик
функции приведён на рисунке справа
рафик
функции приведён на рисунке справа
3.
![]() .
.
I.
![]() ;
общего вида; непериодична;
;
общего вида; непериодична;
![]() при
при
![]() и
и
![]() ;
;
![]() ;
;
![]() .
Находим
.
Находим
![]() и
и
![]() :
:
![]() ;
;
![]() ,
асимптот нет. Первый эскиз графика
функции приведён справа.
,
асимптот нет. Первый эскиз графика
функции приведён справа.
I I.
I.
![]() ,
критические точки первого рода
,
критические точки первого рода
![]() ,
,
![]() .
Таблица изменения знаков производной:
.
Таблица изменения знаков производной:
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
|
|
|
|
Мin=0 |
|
Mах=1 |
|
О тмечаем,
что первый эскиз неправильно описывает
поведение функции в окрестности точки
0.
тмечаем,
что первый эскиз неправильно описывает
поведение функции в окрестности точки
0.
III.
![]() .
.
![]() для
для
![]() ,
выпуклость графика направлена вверх,
точек перегиба нет.
,
выпуклость графика направлена вверх,
точек перегиба нет.
Окончательный вариант графика:
4.
![]() .
.
I.
![]() ;
общего вида; периодична, период Т=2
;
общего вида; периодична, период Т=2![]() , поэтому достаточно построить функцию
на одном периоде, например, на
, поэтому достаточно построить функцию
на одном периоде, например, на
![]() .
Находим значения функции на концах
этого отрезка:
.
Находим значения функции на концах
этого отрезка:
![]() .
При
.
При
![]()
![]() ;
найдём нули функции:
;
найдём нули функции:
 На
отрезке
На
отрезке
![]() расположены два нуля функции:
расположены два нуля функции:
![]() и
и
![]() .
.
![]() на интервалах
на интервалах
![]() и
и
![]() ,
,
![]() на интервале
на интервале
![]() .
В силу периодичности функции нет
необходимости искать пределы функции
на бесконечности и асимптоты.
.
В силу периодичности функции нет
необходимости искать пределы функции
на бесконечности и асимптоты.
II.
![]() .
Ищем критические точки первого рода:
.
Ищем критические точки первого рода:
![]() при
при
![]() и
и
![]() ,
на отрезке
,
на отрезке
![]() находятся три таких точки:
находятся три таких точки:
![]() ,
,
![]() и
и
![]() .
Характер критических точек определяем
с помощью второй производной:
.
Характер критических точек определяем
с помощью второй производной:
![]()
 ;
;
![]() ,
,
![]() ,
,
![]() ;
точка
;
точка
![]() - точка максимума с
- точка максимума с
![]() ,
точка
,
точка
![]() - точка минимума с
- точка минимума с
![]() .
Для определения характера точки
.
Для определения характера точки
![]() найдём
найдём
![]()
![]() ,
,
![]() .
Первая отличная от нуля производная в
точке
.
Первая отличная от нуля производная в
точке
![]() имеет нечётный порядок, т.е. в этой точке
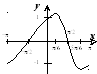
экстремума нет. Всю информацию отражаем
на эскизе графика.
имеет нечётный порядок, т.е. в этой точке
экстремума нет. Всю информацию отражаем
на эскизе графика.
III.
Находим критические точки второго рода:
![]() ,
на отрезке
,
на отрезке
![]() находятся четыре точки, удовлетворяющие
этим уравнениям (в порядке возрастания):
находятся четыре точки, удовлетворяющие
этим уравнениям (в порядке возрастания):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Каждая из этих точек является точкой
перегиба, так как вторая производная
.
Каждая из этих точек является точкой
перегиба, так как вторая производная
![]() меняет знак при переходе через к
меняет знак при переходе через к аждый
свой нуль. Эти точки разбивают отрезок
аждый
свой нуль. Эти точки разбивают отрезок
![]() на пять подмножеств; мы уже определяли
знак второй производной в точке
на пять подмножеств; мы уже определяли
знак второй производной в точке
![]() ,
принадлежащей четвёртому подмножеству,
и в точке
,
принадлежащей четвёртому подмножеству,
и в точке
![]() ,
принадлежащей пятому подмножеству, по
этой информации без труда определяются
направления выпуклости графика функции
на каждом из пяти интервалов. Окончательный
график функции на отрезке
,
принадлежащей пятому подмножеству, по
этой информации без труда определяются
направления выпуклости графика функции
на каждом из пяти интервалов. Окончательный
график функции на отрезке
![]() :
: