9.3. Рациональные функции и их разложение в сумму простых дробей.
9.3.1.
Определение рациональных функций и
простых дробей.
Рациональной функцией называется
отношение двух многочленов
 .
.
Здесь и дальше мы
снова будем работать только с действительной
переменной  ,
коэффициенты обоих многочленов -
действительные числа,
,
коэффициенты обоих многочленов -
действительные числа,  ,
,
 .
Рациональная функция (дробь) называется
правильной, если
.
Рациональная функция (дробь) называется
правильной, если  ;
если
;
если  ,
рациональная дробь называется
неправильной. Любая неправильная дробь
может быть представлена в виде сумма
многочлена степени
,
рациональная дробь называется
неправильной. Любая неправильная дробь
может быть представлена в виде сумма
многочлена степени  и правильной дроби:
и правильной дроби:  ,
,
 ;
нахождение целой части
;
нахождение целой части  и остатка
и остатка  может быть выполнено, например, с помощью
процедуры деления "уголком". В
дальнейшем будем предполагать, что
может быть выполнено, например, с помощью
процедуры деления "уголком". В
дальнейшем будем предполагать, что  - правильная дробь.
- правильная дробь.
Простыми дробями
называются рациональные функции
следующих четырёх типов:
9.3.2.
Теорема о разложении правильной
рациональной функции в сумму простых
дробей. Пусть
знаменатель правильной рациональной
дроби представлен, согласно утверждению
6 пункта 9.2.3,
в виде  ,
,
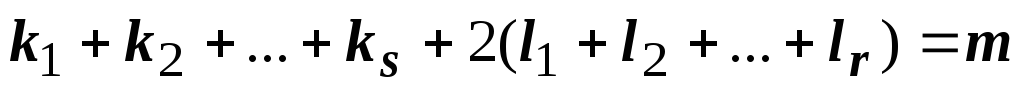 .
Тогда дробь
.
Тогда дробь 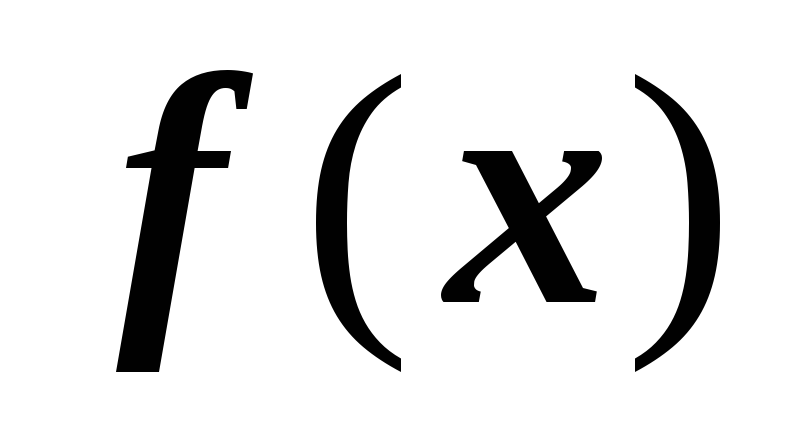 единственным (с точностью до порядка
слагаемых) образом может быть представлена
как суммы простых дробей следующей
структуры
единственным (с точностью до порядка
слагаемых) образом может быть представлена
как суммы простых дробей следующей
структуры
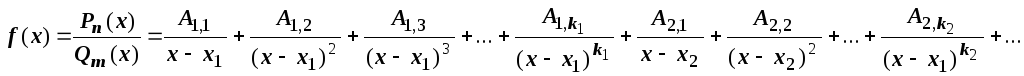
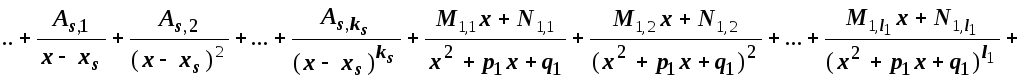
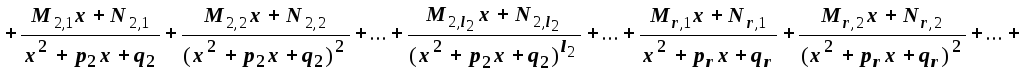
 .
.
Проиллюстрируем
представление неправильной дроби в
виде суммы многочлена и правильной
дроби, и разложение правильной дроби
на простые на примере. Дана функция  .Здесь
.Здесь  ,
, .После деления
"уголком" получим
.После деления
"уголком" получим  .Согласно теореме,
получившаяся правильная дробь должна
представляться в виде
.Согласно теореме,
получившаяся правильная дробь должна
представляться в виде
 ,
(*)где
,
(*)где 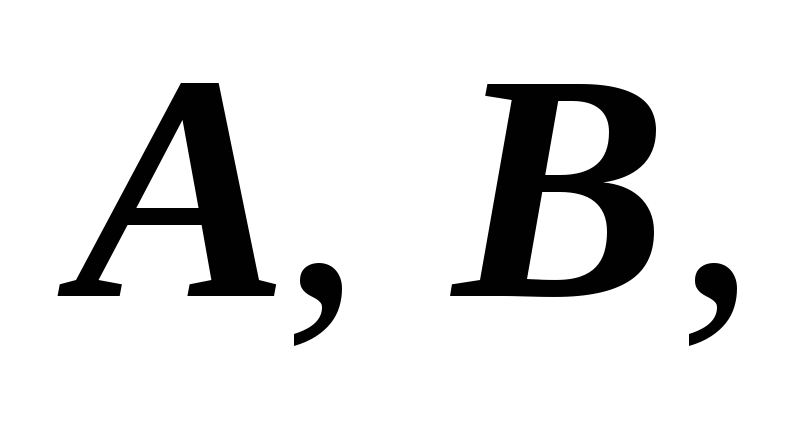
 -
неизвестные пока коэффициенты
("неопределённые коэффициенты").
Приводим сумму в правой части равенства
(*) к общему знаменателю:
-
неизвестные пока коэффициенты
("неопределённые коэффициенты").
Приводим сумму в правой части равенства
(*) к общему знаменателю:
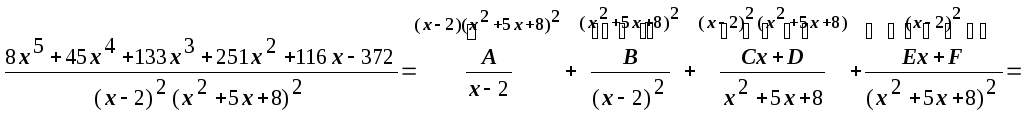
=
 .Дроби в правой и
левой частях этого равенства равны, так
как их знаменатели совпадают, должны
быть равны и числители:
.Дроби в правой и
левой частях этого равенства равны, так
как их знаменатели совпадают, должны
быть равны и числители: 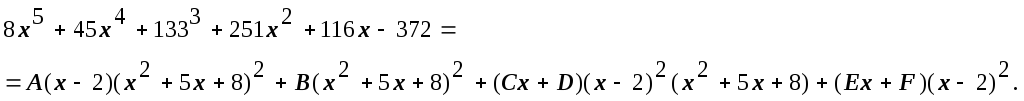
Неопределённые
коэффициенты находятся из этого
равенства. Так, подставив в него значение
 ,
получим
,
получим  .
Если подставить в это равенство корни
трёхчлена
.
Если подставить в это равенство корни
трёхчлена  ,
будут определены
,
будут определены  и
и  .
Такой приём нахождения неопределённых
коэффициентов называют способом частных
значений. Другой метод заключается в
том, что раскрываются скобки в правой
части равенства и приравниваются
коэффициенты при одинаковых степенях
.
Такой приём нахождения неопределённых
коэффициентов называют способом частных
значений. Другой метод заключается в
том, что раскрываются скобки в правой
части равенства и приравниваются
коэффициенты при одинаковых степенях
 :
:
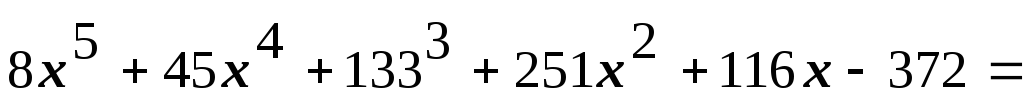
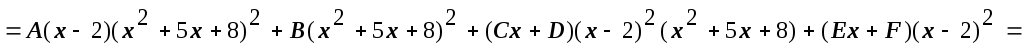
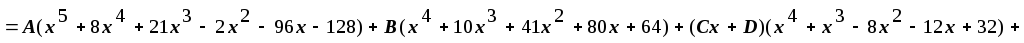
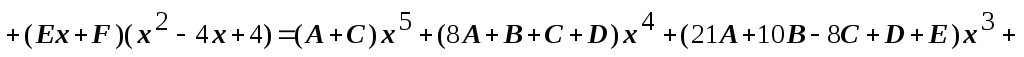
 .
.
Коэффициенты при
степенях
 справа и слева от знака равенства:
справа и слева от знака равенства:
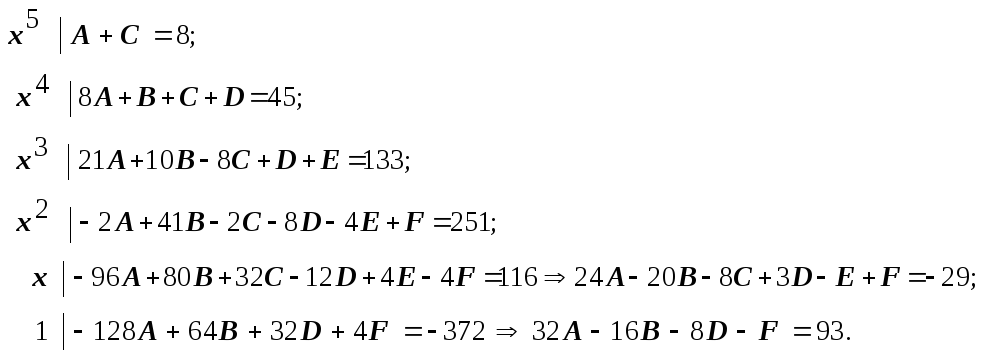
Эту систему можно
решать любым из известных способов.
Воспользуемся правилом Крамера.
 ;
; ;
; ;
;
 ;
; ;
; ;
; ;
;
 ;
; ;
; ;
;
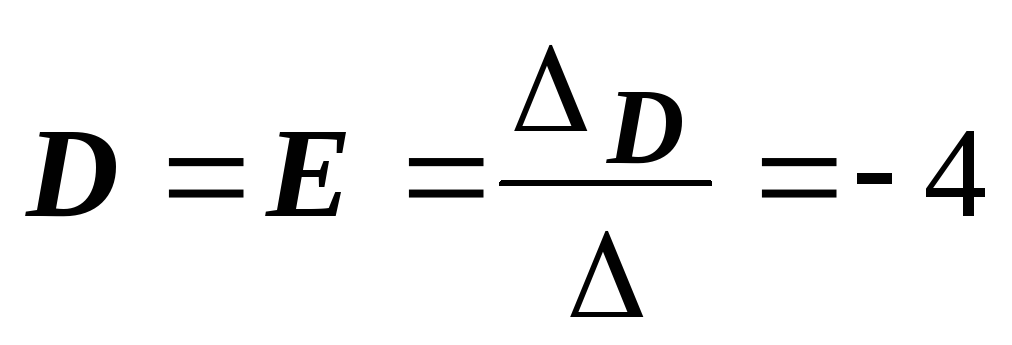 . Окончательно,
функция
. Окончательно,
функция  представляется в
виде
представляется в
виде  .В заключение
отметим, что при решении задач целесообразно
комбинировать методы частных значений
и сравнения коэффициентов при степенях
.В заключение
отметим, что при решении задач целесообразно
комбинировать методы частных значений
и сравнения коэффициентов при степенях
 ,
т.е. исключать коэффициенты, найденные
по частным значениям, из системы
уравнений.
,
т.е. исключать коэффициенты, найденные
по частным значениям, из системы
уравнений.
102


 .
.
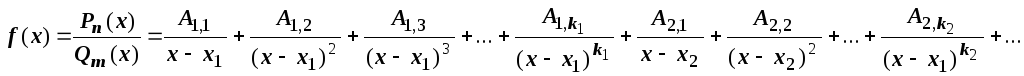
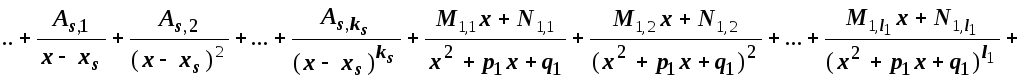
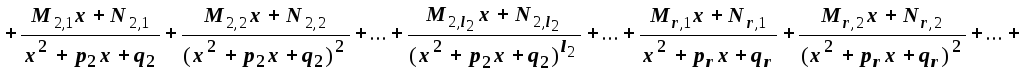
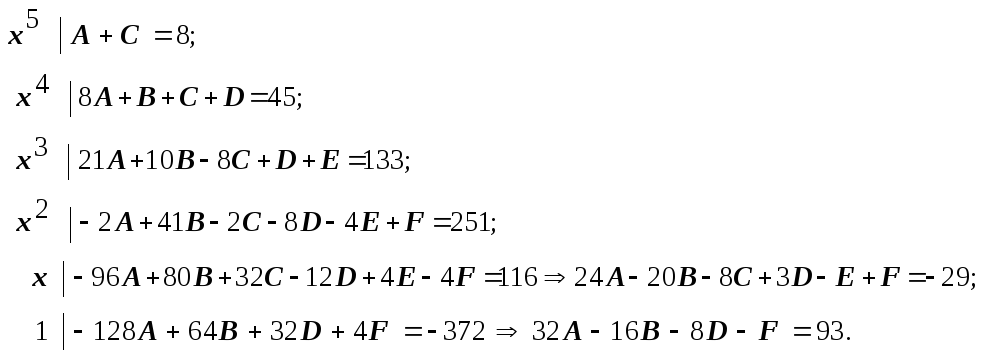
 ;
; ;
; ;
; ;
; ;
; ;
; ;
;