4.5. Решение задач на вычисление пределов.

4.5.1. Непосредственное вычисление пределов.

1. В простейших случаях нахождение предела сводится к подстановке предельного значения аргумента в функцию: если f(x) - элементарная функция, определённая в точке а, то , например ;

2. , если f(х)0 при ха;

3. , если f(х) при ха;

4. , если g(х)0, f(х)  при ха, например и т.д.

Найдём ряд пределов, которые понадобятся впоследствии:

5. Докажем, что 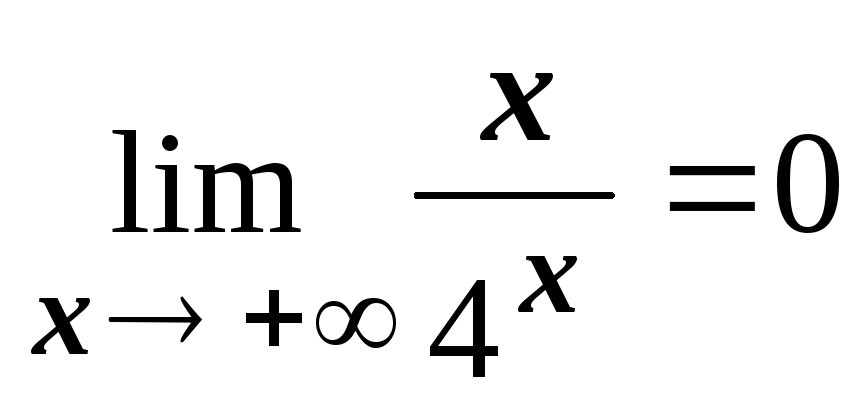. При х + и числитель, и знаменатель стремятся к бесконечности, поэтому пределы такого типа называются неопределённостями . А).При справедливо неравенство (оно справедливо при n=2, далее, по индукции: пусть оно верно при произвольном n, тогда n +1< n + n = 2n <2, т.е. оно верно и при n +1). Следствие: , т.е. последовательность ограничена. Б). Рассмотрим последовательность .

(как предел произведения ограниченной и бесконечно малой последовательностей). В). Пусть х - произвольное вещественное число, x>0. Тогда , где Е(х) - целая часть числа х. Обозначим Е(х)=n. . Устремим х +, тогда и n . Предел постоянной 0 равен этой постоянной, предел правой части . По теореме 4.4.6 о пределе промежуточной функции , что и требовалось доказать. Легко видеть, что это доказательство с небольшими изменениями воспроизводится, если заменить число 4 любым числом а>1, поэтому будем считать доказанным, что при а>1.

5. при а>1 легко сводится к предыдущему. Пусть 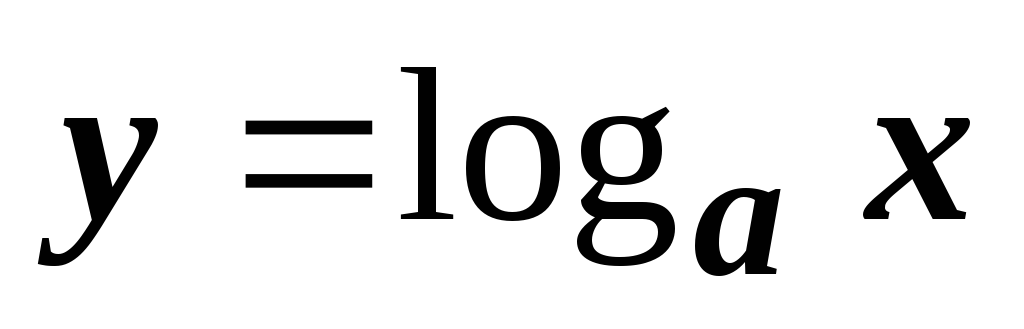, тогда 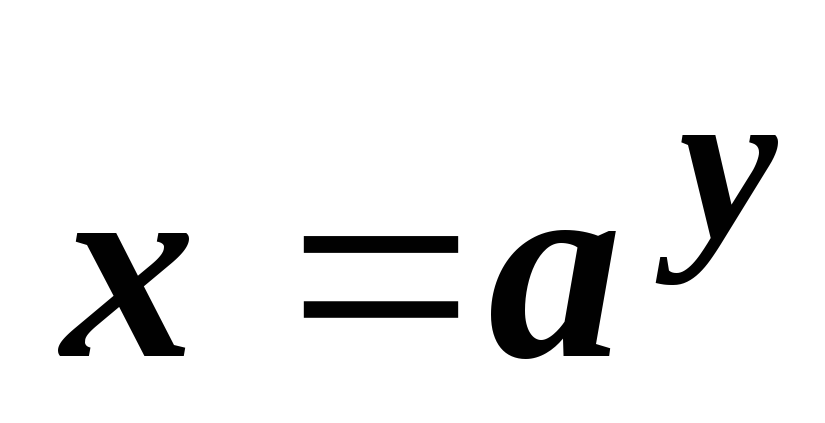, у + при х +, и .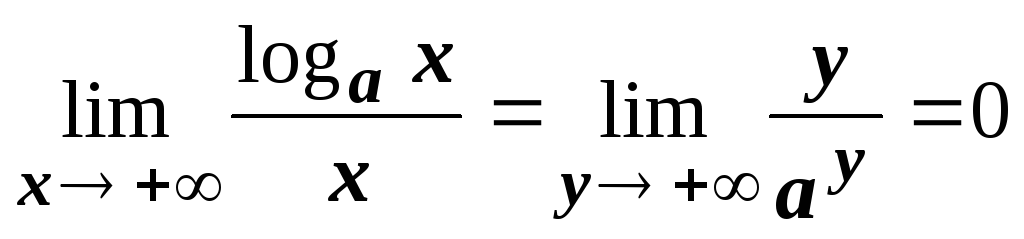

7. Как следствие при а>1, b>1.

8. (неопределённость ) также сводится к первому из рассмотренных пределов. Пусть у=1/х. Тогда х=1/у, у + при х +0, ln x=ln(1/y)=-ln y, поэтому .

4.5.2. Выделение главной части функции.

Выделение главной части функции - мощный приём при решении задач на вычисление пределов. Основная цель выделения главной части - получение более простой функции, которая в окрестности предельной точки ведёт себя также, как исходная громоздкая (тогда по теореме 4.4.9.2 о замене бесконечно малых на эквивалентные мы можем заменить громоздкие функции в числителе и знаменателе на эквивалентные простые); основной инструмент при выделении главных частей - табл. 4.4.10 эквивалентных бесконечно малых.

Как следует из определений разделов 4.4.8-4.4.11, утверждения "при ха 1. f(x)g(x); 2. f(x)-g(x)=o(g(x)) =o(f(x)); 3. g(x) есть главная часть f(x)" эквивалентны. Так как для f(x) может существовать бесконечно много главных частей при ха (например, при х0   …..), при выделении главных частей указывается их вид; при решении задач на вычисление пределов при ха обычно это С₀(х-а)^k для бесконечно малых и для бесконечно больших, прих - это для бесконечно малых идля бесконечно больших, где С₀ = const0, k =const>0 – порядок малости или роста функции f(x) относительно функции (х-а) (или относительно прих). Для главных частей такого вида бесконечно малых при ха функций равносильны следующие утверждения:

1. ;

2. , где(х) – БМ при ха;

3. ;

4. , где;

5. f(x)  .

Таким образом, в простейших случаях рецепт для выделения главной части вида С₀(х-а)^k БМ при ха функции f(x) состоит в следующем: f(x) надо представить в виде f(x)=, где. Тогда, и- главная часть функцииf(x) при ха.

Аналогично изложенному выше, с заменой (х-а)^k на , формулируются утверждения и правило для выделения главной части функции, бесконечно малой прих.

Рассмотрим ряд примеров на выделение главной части и определение порядка малости функций (в скобках указываются применённые формулы табл. 4.4.10):

1. . Представимf(x) в виде . Если, то, поэтому,k=1 – порядок малости f(x) при х0.

2. . Представимf(x) в виде . Если, то, поэтому,k=2 – порядок малости f(x) при х по сравнению с .

3. . С помощью формул 4,6таблицы 4.4.10 представим f(x) в виде . Здесь,, поэтому,k=1 – порядок малости f(x) при х0.

4. . Так какf(-2) = 0, то , и многочленделится нах + 2 без остатка. Произведя деление, получим . Так как иf₁(-2) = 0, то , поэтому, где. Результат:,- главная частьf(x), k=2 – порядок малости f(x) при х-2.

5. ., где. Поэтому,- главная часть,k=5/6 (относительно БМ ) при.

В следующих задачах решение излагается более кратко.

6.

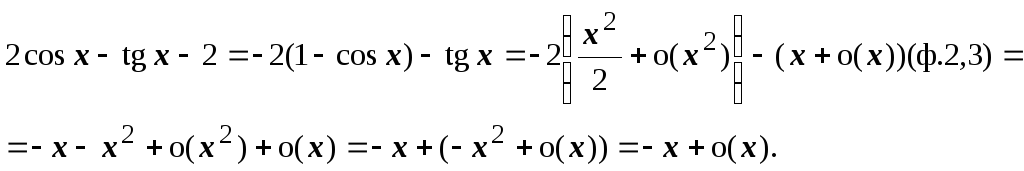
7. .

8. .

9.

Неаккуратность при решении последнего примера даст результат

верный, но бесполезный.

10. Пусть х +0. Тогда

Если рассматривается случай ха  0, часто полезно сделать замену переменной у= х-а.

Пример:

11. Пусть х2. Найти главную часть БМ функции (убедитесь, что f(x) 0 при х2). Перейдём к переменной у= х-2 х= у+2; у0 при х2. Меняем в функции х на у+2:

Так как у0, мы пришли к задаче, рассмотренной в примере 2. Ответ: , при х2.

12. Для функции, представляющей собой линейную комбинацию степенных выражений легко показать, что при х0 f(x) эквивалентна своему слагаемому с минимальной степенью: f(x): и все слагаемые, кроме последнего, стремятся к нулю при х0, так как при i=1,2,…,k-1.

При х f(x) эквивалентна своему слагаемому с максимальной степенью f(x): и все слагаемые, кроме первого, стремятся к нулю при х, так как при i=2,…,k.