6.9. Таблица производных и дифференциалов.

Соберём полученные в разделах 6.2, 6.3, 6.5 выражения для производных и следующие из них выражения для дифференциалов в одну таблицу:

№	y(x)	y'(x)	dy		№	y(x)	y'(x)	dy
1	y = C	0	0		10
2	у = ха	a ха-1	a ха-1dx		11
3					12
3a					14
4					15
4a					16
5					17
6					18
7					19
8					20
9					21

6.10. Производные функций, заданных параметрически и неявно.

6.10.1. Производные функций, заданных параметрически. Пусть зависимость у от х задана через параметр t: , обе эти функции дифференцируемы, и для первой из них существует обратная функция . Тогда явная зависимость у от х выражается формулой. Находим производную: . Здесь мы воспользовались результатами разделов 6.5.5. Производная сложной функции и 6.3. Производная обратной функции. То же выражение можно получить из 6.8.2. Инвариантности формы первого дифференциала: .

Примеры:

1. . Тогда . В этом примере легко получить явную зависимость у от х: . Подставим сюда зависимость х от t: . Как и следовало ожидать, получен тот же результат.

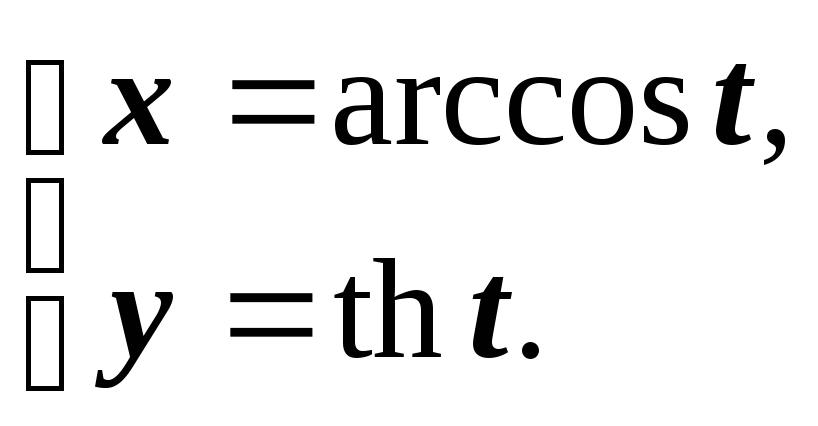2. . Тогда .

6.10.2. Производные функций, заданных неявно. Неявным заданием зависимости у от х называется уравнение вида F(x,y) = 0, связывающее эти две переменные. Общая формула для y'(x), следующая из неявного уравнения F(x,y) = 0, включает в себя частные производные, которые мы будем изучать позже; пока приведём несколько примеров, показывающих, как найти производную y'(x) из неявного уравнения.

1. . Дифференцируем это равенство по х, учитывая зависимость у от х (применяя правило дифференцирования сложной функции: ):

. Легко понять, что при этом всегда получится уравнение, линейное относительно y'(x), которое без труда решается: . Производная найдена, она совпадает с полученной в предыдущем разделе (с учётом явного выражения ).

2. . Дифференцируем по х, учитывая зависимость у от х:

.

Решаем это уравнение относительно y': .

6.11. Производные и дифференциалы высших порядков.

6.11.1. Производные высших порядков. Формула Лейбница. Пусть функция имеет производную y'(x) в каждой точке интервала (а,b). Функция y'(x) тоже может иметь производную в некоторых точках этого интервала. Производная функции y'(x) называется второй производной (или производной второго порядка) функции и обозначается . Функция y''(x) тоже может иметь производную, которая называется третьей производной (или производной третьего порядка) функции и обозначается . Вообще n-ой производной (или производной n-ого порядка) функции называется производная от производной n-1-го порядка (обозначения: ).

Производные высших порядков последовательно вычисляются по уже известным формулам и правилам. Пусть, например, . Тогда , , , и т.д. В некоторых случаях можно получить общее выражение для n-ой производной функции: пусть . Тогда , , , и вообще . Аналогичную формулу можно получить для косинуса. Другой пример: . Если представить эту функцию в виде , то ,, и вообще .

Для высших производных произведения функций справедлива формула Лейбница:

. Эта формула внешне похожа на формулу бинома Ньютона и, также как формула бинома Ньютона, может быть доказана методом математической индукции. Для низших производных:

; ; .

6.11.2. Дифференциалы высших порядков также определяются индуктивно: дифференциалом второго порядка (или вторым дифференциалом) функции называется дифференциал от её первого дифференциала; дифференциалом третьего порядка называется дифференциал от второго дифференциала; и вообще, дифференциалом n-го порядка функции называется дифференциал от её n-1-го дифференциала. При вычислении высших дифференциалов необходимо учитывать, что дифференциал независимой переменной - произвольная и независимая от х величина, которая при дифференцировании рассматривается как постоянная. Поэтому ; ; …., .

6.11.3. Неинвариантность формы старших дифференциалов относительно замены переменной. В разделе 6.8.2. Инвариантность формы первого дифференциала мы доказали, что независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же: dy = y'dx. Покажем, что уже второй дифференциал этим свойством не обладает. Если х - независимая переменная, то d ²y = y"dx². Если x = (t), то d ²y = d(dу) = d(y'_хdx) =

= d(y'_х)dx + y'_хd(dx). Для первого слагаемого вследствие инвариантности формы первого дифференциала d(y'_х) = y"_ххdx, для второго d(dx) = d ²x, поэтому окончательно d ²y = y"_ххdx²+ y'_хd ²x, что отличается от случая независимой переменной. Причина этого понятна: если х независимая переменная, то при нахождении второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t) дифференциал dx определяется дифференциалом dt.

6.11.4. Старшие производные функции, заданной параметрически. В разделе 6.10.1. Производные функций, заданных параметрически, для первой производной функции

была получена формула . Если применить эту формулу к функции

то получим: ; аналогично, применяя ту же формулу ко второй производной, получим выражение для третьей производной, и т.д. Так, для функции мы получили . Найдем вторую производную: .

6.11.5. Старшие производные функции, заданной неявно, находятся последовательно, в соответствии с определением старших производных. Так, для неявно заданной зависимости у от х мы получили . Найдём вторую производную: . Дальше можно найти третью и т.д. производные.

67