6.8. Дифференцируемость функций. Дифференциал.

6.8.1. Определение дифференцируемости и дифференциала. Пусть функция y = f(x) определена в точке х и некоторой окрестности этой точки и непрерывна в точке х. Тогда приращению х аргумента соответствует приращение у = f(x+х)- f(x), бесконечно малое при х0. В особый класс дифференцируемых функций выделяются функции, для которых у с точностью до бесконечно малой высшего порядка по сравнению с х линейна по х. Более точно:

Опр.6.2. Функция y = f(x) называется дифференцируемой в точке х, если её приращение у в этой точке можно представить в виде , где А - не зависящая от х величина, (х) - БМ высшего порядка по сравнению с х: при х0.

В более краткой записи для дифференцируемой в точке х функции .

Опр.6.3. Главная часть приращения у дифференцируемой функции, линейная относительно приращения х аргумента (т.е. ), называется дифференциалом функции и обозначается dy (или df(x)).

Связь между дифференцированием и дифференцируемостью даёт

Теор.6.4. Для того, чтобы функция y = f(x) имела в точке х конечную производную

y' = f'(x), необходимо и достаточно, чтобы она была дифференцируемой в этой точке.

Док-во. Необходимость. Пусть в точке х существует конечная производная y'. По теор.6.2 о приращении функции, имеющей производную, у= у'(x) х + (х) х, где (х) - бесконечно малая функция при х 0. Сравнивая это выражение с определением 6.2, делаем вывод: А= у'(x), БМ (х) х имеет более высокий порядок по сравнению с х, т.е. f(x) действительно дифференцируема в точке х.

Достаточность. Пусть f(x) дифференцируема в точке х, т.е. её приращение у можно представить в виде , где А - не зависящая от х величина, (х) - БМ высшего порядка по сравнению с х: при х0. Тогда . Следовательно, существует предел отношения приращения функции к приращению аргумента, т.е.  у'(x), и у'(x)=А.

Таким образом, для функции одной переменной существование производной и дифференцируемость - эквивалентные свойства. При этом коэффициент А всегда равен у'(x), и выражение для дифференциала приобретает вид dy = у'(x) х. Для независимой переменной х принимают dх= =х (формально это можно обосновать так: если у=х, то у'(x)=1, и dy = dх = х). Итак, окончательное выражение для дифференциала имеет вид .

Важно осознать, что в этом выражении не обязательно понимать dх как бесконечно малую, dх - произвольное не зависящее от х приращение аргумента (но именно при dх0 и dу0, и призведение у'(x)dх = dy становится главной частью приращения функции). Так как у'(x)=tg() - угловой коэффициент касательной, то геометрически дифференциал dy - это приращение ординаты касательной при смещении абсциссы на dх =х. Значение dy может значительно отличаться от приращения функции у, но при достаточно малых х (в окрестности точки касания) они близки (участок АВ графика функции).

6.8.2. Инвариантность формы первого дифференциала. Здесь мы рассмотрим одно важное свойство дифференциала, следующее из формулы для производной сложной функции (раздел 6.5.5. Производная сложной функции): если функции и имеют в соответствующих точках производные и , то производная сложной функции равна .

Если х - независимая переменная, то формула для дифференциала: . Если , то . Таким образом, независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же. Это свойство и называется инвариантностью формы первого дифференциала, и часто применяется в теории и решении задач. Ниже (раздел 6.10) мы с помощью этого свойства выведем формулу для производной функции, заданной параметрически.

6.8.3. Правила для вычисления дифференциала. Примеры вычисления дифференциала. Правила для вычисления дифференциала - прямое следствие правил дифференцирования (раздел 6.5):

1. ;

2. ;

3. ;

4. .

Докажем, для примера, формулу 3: .

При нахождении дифференциала можно вычислить производную и затем применить формулу :

, поэтому ;

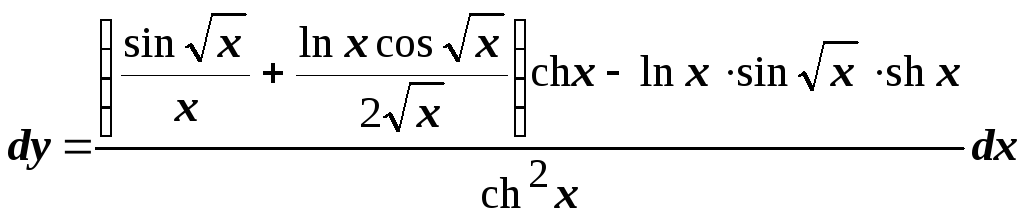но более квалифицированным является прямое применение правил вычисления дифференциала:

6.8.4. Применение дифференциала в приближённых вычислениях. Именно близость исходной функции и её касательной в окрестности точки касания служит источником многочисленных приближённых формул для вычисления значений функций. По теор.6.2 (раздел 6.4. Формула для приращения функции, имеющей производную) у= у'(x) х + (х) х, где (х) - БМ при х 0; с учётом того, что у'(x) х = у'(x)dх = dy, пренебрегая бесконечно малым слагаемым высшего порядка по сравнению с х, получим у  dу. Так как у=у(x+х)- у(x), то формула для приближённого значения у(x+х) будет иметь вид у(x+х)  у(x)+ у'(x) х. На практике этой формулой пользуются так. Пусть требуется вычислить значение функции в точке х₁. Подбирают близкую к точке х₁ точку x, в которой легко вычислить точное значение у(x) и у'(x), тогда х = х₁- х и у(x+х)  у(x)+ у'(x) х. Примеры:

1. Вычислить . В этом случае , функция и производная легко вычисляется в близкой точке х=32, у(х)=2, у'(х)=1/(5*2⁴)=1/80, х₁=30, х =30-32= -2, и

2-2/80 = 1.975 (более точное значение 1.97435).

2. Вычислить sin(0.5). y(x)=sinx, y'(x)=cosx, в качестве х примем x = /60.524, х₁=0.5,

х =0.5-0.524= -0.024, y(x)=0.5, y'(x)=0.866, y(х₁)  0.5 - 0.024*0.8660.5-0.021=0.479 (более точное значение 0.47943).