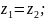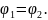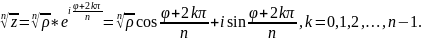- •Рисуночек(pict002)
- •7)Задача про роботу силового поля. Робота силового поля обчислюється двома шляхами: 1)в основу покладена властивість адитивності 2)основою даного розв’язку є формула Гріна: , де ;
- •4)Теор про середнє значення функції для потрійного інтегралу. Якщо функція f(X,y,z) – неперервна в замкнутій області , то існує точка в якій
- •9)Потрійні інтеграли у сферичних координатах. З маємо Отже, Обчислюємо якобіан переходу
- •10)Застосування потрійних інтегралів у геометрії та механіці. 1)Обчислення об’єму тіла.Якщо тіло однорідне і густина то об’єм дорівнює :
- •2)Координати центра мас тіла:
- •3)Момент інерції тіла відносно координатних осей:
- •2) Комплексні числа в тригонометричній та показниковій формах.
- •6)Основні властивості інтеграла від фкз, теорема Коші. Вони випливають з означення цього інтеграла:
- •Довжина .
- •1) Властивість лінійності перетворення Лапласа. Зображення функцій . T.Якщо , ,а і дійсні сталі то, ;і взагалі
- •7) Теор про інтегрування оригіналу.
1)Комплексні
числа в алгебраїчній формі(озн, який
вигляд,дії над ними).
Комплексне число Z
це вираз z=x+iy,
де
x,y-
дійсні,
і-уявна одиниця
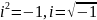 .
x=Re
z
–
реальна частина
, y=Im
z
– уявна
частина.
.
x=Re
z
–
реальна частина
, y=Im
z
– уявна
частина.
 -
спряжене до z.
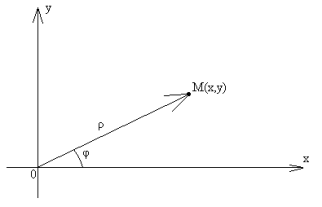
Комплексне число z
зображується на площині XoY
точкою M(x,y)
або
вектором
-
спряжене до z.
Комплексне число z
зображується на площині XoY
точкою M(x,y)
або
вектором
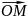 .
Довжина цього вектора
.
Довжина цього вектора
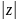 називається
модулем комплексного числа. Кут між
вектором
і оX
позначається Arg
z
і називається аргументом. Значення
аргумента в межах (-П;П) називається
головним і позначається аrg
z.
називається
модулем комплексного числа. Кут між
вектором
і оX
позначається Arg
z
і називається аргументом. Значення
аргумента в межах (-П;П) називається
головним і позначається аrg
z.
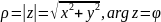 ,
,
 полярні
координати точки М. Операції над
комплексними числами :
полярні
координати точки М. Операції над
комплексними числами :
Нехай
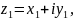
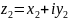 1)
1)
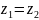 лише тоді , коли
лише тоді , коли


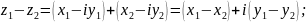
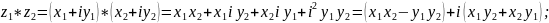
z*
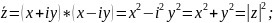
 =
= =
= .
.
2) Комплексні числа в тригонометричній та показниковій формах.
Скористаємось формуло Ейлера:
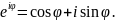
 .
.
Операції над комплексними числами у цих формах
Нехай

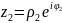
3)ФКЗ – озн, одномістність(?), неперервність в точці і в області, диференційованість. Комплексне число Z це вираз z=x+iy, де x,y- дійсні, і-уявна одиниця . x=Re z – реальна частина , y=Im z – уявна частина.
- спряжене
до z.
Будемо
називати W
функцією незалежної змінної z.
Якщо кожному z
з області D
відповідає комплексне значення W
, то z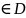 ,
W=u+iv,
W=f(z).
Ця функція відображає область
комплексної
площини Z.
u=u(x,y),
v=v(x,y).
,
W=u+iv,
W=f(z).
Ця функція відображає область
комплексної
площини Z.
u=u(x,y),
v=v(x,y).
Якщо
при
 виконується
умова
виконується
умова
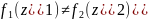 ,
то функція W=f(z)
називається одномісною.
,
то функція W=f(z)
називається одномісною.
Функція
W=f(z)
називається неперервною в точці
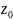 якщо для всіх точок достатньо малого
околу точки
і відповідні значення функції належать
малому околу
якщо для всіх точок достатньо малого
околу точки
і відповідні значення функції належать
малому околу
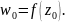 Функція
неперервна в області якщо вона неперервна
в кожній точці цієї області. Дії
додавання, віднімання , множення, ділення
(знаменник не дор. 0) дають неперервні
функції.Функція
W=f(z)
називається диференційованою в точці
z
області
D
, якщо існує скінченна границя відношень
Функція
неперервна в області якщо вона неперервна
в кожній точці цієї області. Дії
додавання, віднімання , множення, ділення
(знаменник не дор. 0) дають неперервні
функції.Функція
W=f(z)
називається диференційованою в точці
z
області
D
, якщо існує скінченна границя відношень
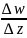 ,
коли
,
коли
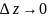 при
при
 .
.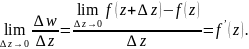
4)Диференціюв-ня
ФКЗ, умови Коші-Рімана.
Функція W=f(z)
називається диференційованою в точці
z
області
D
, якщо існує скінченна границя відношень
,
коли
при
.
Однозначна функція аналітична в області
D
, якщо в кожній точці цієї області вона
має скінченну похідну. Ці функції мають
спеціальні властивості. Правила
диференціювання такі ж як і для функцій
дійсних змінних .Будь-яка диференційовна
в точці z
функція W=f(z)
– неперервна в цій точці.Умови
Коші-Рімана. Нехай f(z)
має похідну.
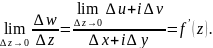 Так як
довільним чином, то
Так як
довільним чином, то
 .Маємо:
.Маємо:
 .Аналогічно
одержуємо:
.Аналогічно
одержуємо: ;
;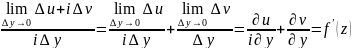 ;
; ;
;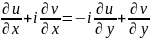 ;
;
 ;
; ;
;
5)Інтеграл
від ФКЗ – озн та обчислення.
Нехай
Функція W=f(z)
– неперервна функція комплексної
змінної z,
яка визначена в області D
і
 - довільна гладк
- довільна гладк а
лінія в цій області. Розіб’ємо АВ на
довільне число n
елементарних дуг
а
лінія в цій області. Розіб’ємо АВ на
довільне число n
елементарних дуг
 в
додатному напрямку від А до В . Позначимо
в
додатному напрямку від А до В . Позначимо


Доведемо
що (1) прямує до скінченної границі, яка
не залежить від того закону за яким
елементарні дуги прямують до нуля.
Введемо такі позначення:

 .
.
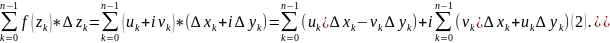 Коли
Коли
 ,
то обидві суми в (2) прямують до відповідних
границь:
,
то обидві суми в (2) прямують до відповідних
границь:
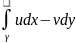 та
та
 .Отже,
ліва частина (2) теж прямує до скінченної
границі. Її називають інтегралом функції
f(z)
по кривій
.
.Отже,
ліва частина (2) теж прямує до скінченної
границі. Її називають інтегралом функції
f(z)
по кривій
.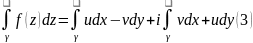
У
правій частині маємо два дійсних
інтеграла другого роду. Для запам’ятовування
запишемо так:

Обчислення
інтегралів Нехай рівняння кривої
: z=z(t);
.
Тоді
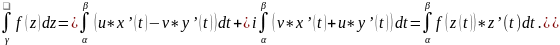 або
або
 де
де
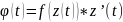
Таким чином в обчисленні інтеграла від функції f(z) зводиться до обчислення двох звичайних визначених інтегралів по t.
6)Основні властивості інтеграла від фкз, теорема Коші. Вони випливають з означення цього інтеграла:


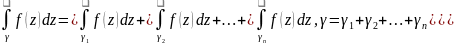
 =
=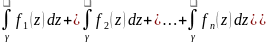
Довжина .
Доведення
 Теорема
Коші.Якщо функція f(z)
– однозначна в однозв’язній області
D
і має в кожній точці цієї області
неперервну похідну , то інтеграл цієї
функції вздовж замкненого контура
,
що належить області D,
дорівнює нулю.
Теорема
Коші.Якщо функція f(z)
– однозначна в однозв’язній області
D
і має в кожній точці цієї області
неперервну похідну , то інтеграл цієї
функції вздовж замкненого контура
,
що належить області D,
дорівнює нулю.
Доведення. З умови теореми випливає що u(x,y) та v(x,y) неперервні разом зі своїми частинними похідними в області D. Отже, виконуються умови Коші-Рімана:
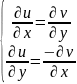 ;Нехай
– довільний замкнутий контур , тоді
;Нехай
– довільний замкнутий контур , тоді
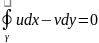 ,то
,то

7)Інтегральна
формула Коші.
Нехай
D
односвязна область що обмежена довільною
кусково-гладкою кривою Г і f(z)
– функція яка аналітична в замкнутій
області
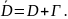 Це означає, що f(z)
має визначену скінченну похідну в
кожній точці деякої області G,
яка містить
Це означає, що f(z)
має визначену скінченну похідну в
кожній точці деякої області G,
яка містить
 .
Формула Коші виражає значення функції
f(z)
у деякій точці z,
внутрішньо відносно Г , через значення
цієї функції на контурі Г. Вона має
такий вигляд:
.
Формула Коші виражає значення функції
f(z)
у деякій точці z,
внутрішньо відносно Г , через значення
цієї функції на контурі Г. Вона має
такий вигляд:
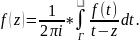 Інтегрування іде у додатному напрямі.
Для доведення розглянемо допоміжну
функцію:
Інтегрування іде у додатному напрямі.
Для доведення розглянемо допоміжну
функцію:
 Ця функція аналітична всюди, крім точки
t=z.
Опишемо контур радіуса ρ навколо точки
z.
Тоді функція
Ця функція аналітична всюди, крім точки
t=z.
Опишемо контур радіуса ρ навколо точки
z.
Тоді функція
 аналітична у кільці.За теоремою Коші
для складеного контура маємо:
аналітична у кільці.За теоремою Коші
для складеного контура маємо:
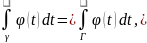 не залежить від радіуса ρ і дорівнює
сталому числу
не залежить від радіуса ρ і дорівнює
сталому числу
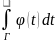 .Далі
маємо
.Далі
маємо
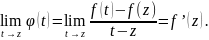 Отже, якщо прийняти
Отже, якщо прийняти
 як значення функції
в точці t=z,
то
стає неперервною всюди в
і можна стверджувати , що
як значення функції
в точці t=z,
то
стає неперервною всюди в
і можна стверджувати , що
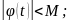 М=const.
Для будь-якої точки t
.
Користуючись цією нерівністю і
властивістю
М=const.
Для будь-якої точки t
.
Користуючись цією нерівністю і
властивістю
 .
.
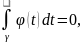 тому що ρ можна взяти як завгодно
малим, а значення інтеграла – стале
число, тому
тому що ρ можна взяти як завгодно
малим, а значення інтеграла – стале
число, тому
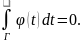 Замінюєм
її значенням і одержимо:
Замінюєм
її значенням і одержимо:
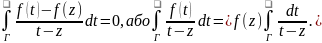 Очислимо
останній інтеграл( t-
змінна, z-
const)
;
Очислимо
останній інтеграл( t-
змінна, z-
const)
;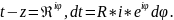
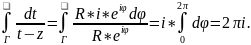 ;
;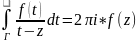 ;
;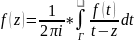 ;
;
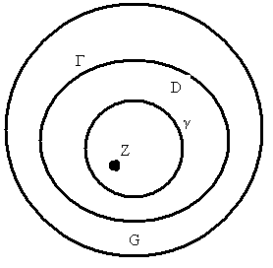
8)Інтегральне
зображення похідних аналітичної
функції(інтеграли типу Коші).
Функція F(z)
, що визначена за допомогою інтеграла
типу Коші
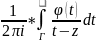 ,
є аналітична у всякій однозв’язній
області D,
яка не містить точок лінії L,
а для її похідної має місце формула:
F’(z)=
,
є аналітична у всякій однозв’язній
області D,
яка не містить точок лінії L,
а для її похідної має місце формула:
F’(z)= .Доведення: Розглянемо відношення
.Доведення: Розглянемо відношення
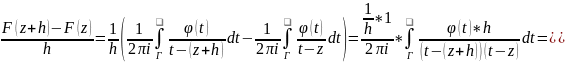 [Переходимо
до границь при h
[Переходимо
до границь при h 0:]
0:]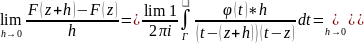 [Скористаємось теоремою про перехід
до границі в інтегралі, що залежить від
параметра h.]
[Скористаємось теоремою про перехід
до границі в інтегралі, що залежить від
параметра h.] Функція F(z),
що визначена за допомогою інтеграла
Коші має в кожній точці z,
яка лежить ззовні лінії L,
похідні всіх порядків, для яких мають
місце формули:
Функція F(z),
що визначена за допомогою інтеграла
Коші має в кожній точці z,
яка лежить ззовні лінії L,
похідні всіх порядків, для яких мають
місце формули:

9) Ряд
Тейлора для аналітичної функції.
Якщо функція f(z)
аналітична в крузі
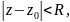 то в цьому крузі має місце рівність :
то в цьому крузі має місце рівність :
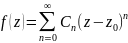 (1) , де
(1) , де
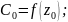
 … ;
… ;
 (2) або
(2) або
 ;
;
 (3). При чому Г – будь-який замкнутий
контур , що лежить всередині круга
радіуса R
з точкою в центрі
.
Нехай z
– будь-яка точка круга радіуса R
. Візьмемо коло
так, щоб воно лежало всередині круга
і містило точку z.
Оскільки f(z)
– аналітична функція , то згідно формули
Коші маємо
(3). При чому Г – будь-який замкнутий
контур , що лежить всередині круга
радіуса R
з точкою в центрі
.
Нехай z
– будь-яка точка круга радіуса R
. Візьмемо коло
так, щоб воно лежало всередині круга
і містило точку z.
Оскільки f(z)
– аналітична функція , то згідно формули
Коші маємо
 .
В знаменнику віднімемо і додамо
:
.
В знаменнику віднімемо і додамо
:
 |маємо суму нескінченно спадної
геометричної прогресії
|маємо суму нескінченно спадної
геометричної прогресії
 |
|
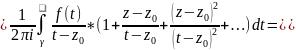 | Одержаний в дужках ряд можна почленно
інтегрувати так як він збігається
рівномірно, бо маємо мажоранту
геометричної прогресії |
| Одержаний в дужках ряд можна почленно
інтегрувати так як він збігається
рівномірно, бо маємо мажоранту
геометричної прогресії |
 де коефіцієнт
де коефіцієнт
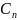 визначається
рівністю (2). Згідно інтегрально форми
Коші контур
можна замінити на Г. Зауваження 1.
Представлення функції f(z)
рядом
Тейлора єдине в околі даної точки
.Зауваження
2. Для знаходження Ряду Тейлора
використовуємо основні розклади
визначається
рівністю (2). Згідно інтегрально форми
Коші контур
можна замінити на Г. Зауваження 1.
Представлення функції f(z)
рядом
Тейлора єдине в околі даної точки
.Зауваження
2. Для знаходження Ряду Тейлора
використовуємо основні розклади
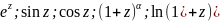 .
Рисуночек(pict003)
.
Рисуночек(pict003)
10)Ряд
Лорана (без дов). Класифікація ізольованих
особливих точок однозначної аналітичної
функції.
Теорема. Нехай функція
f(z)
– аналітична і однозначна в кільці
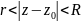 .
Тоді у будь-які точці z,
що належить кільцю , цю функцію можна
представити у вигляді ряду Лорана за
додатніми і від’ємними степенями
бінома
.
Тоді у будь-які точці z,
що належить кільцю , цю функцію можна
представити у вигляді ряду Лорана за
додатніми і від’ємними степенями
бінома

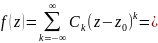 |Запишемо ряд у розгорнутому вигляді|
|Запишемо ряд у розгорнутому вигляді|
 .Цей ряд складається з головної частини,
яка містить від’ємні степені бінома
і правильної частини , що містить
невід’ємні степені бінома
.
Представлення функції рядом Лорана
єдине.Класифікація
ізольованих особливих точок однозначної
аналітичної функції. Особливі точки –
це ті, в яких порушується умова
аналітичності функції.Точка
– ізольовано особлива, якщо ряд Лорана
збігається в області
.Цей ряд складається з головної частини,
яка містить від’ємні степені бінома
і правильної частини , що містить
невід’ємні степені бінома
.
Представлення функції рядом Лорана
єдине.Класифікація
ізольованих особливих точок однозначної
аналітичної функції. Особливі точки –
це ті, в яких порушується умова
аналітичності функції.Точка
– ізольовано особлива, якщо ряд Лорана
збігається в області
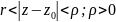 .Особливі
точки класифікуються за допомогою
головної частини ряду Лорана. Є 3 типи
особливих точок:1)Точка
-
називається усувною особливою точкою,
якщо головної частини ряду Лоран немає
зовсім. При чому
.Особливі
точки класифікуються за допомогою
головної частини ряду Лорана. Є 3 типи
особливих точок:1)Точка
-
називається усувною особливою точкою,
якщо головної частини ряду Лоран немає
зовсім. При чому
 .2)Точка
.2)Точка
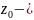 полюс кратності «n»,
якщо головна частина має скінченне
число «n»
доданків для функції
полюс кратності «n»,
якщо головна частина має скінченне
число «n»
доданків для функції
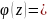 маємо:
маємо:
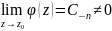 .
Якщо «n»=1,
то маємо простий полюс. Полюси знаходимо
з рівняння:
.
Якщо «n»=1,
то маємо простий полюс. Полюси знаходимо
з рівняння:
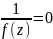 ;
;
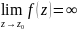 ;3)Коли
кількість від’ємних степенів бінома
у головній частині ряда Лорана
нескінченна, то
називається істотно особливою точкою.
В цьому випадку
;3)Коли
кількість від’ємних степенів бінома
у головній частині ряда Лорана
нескінченна, то
називається істотно особливою точкою.
В цьому випадку
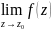 - не існує.
- не існує.
11)Лишки
аналітичної функції - озн та обчисл.
Лишком аналітичної функції
 у нескінченно віддаленій точці
у нескінченно віддаленій точці
 називається коефіцієнт при
називається коефіцієнт при
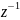 в розкладі цієї функції в ряд Лорана,
взятий з протилежним знаком.1)Нехай
в розкладі цієї функції в ряд Лорана,
взятий з протилежним знаком.1)Нехай
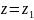 -
простий полюс функції
,
тоді вона має такий ряд Лорана :
-
простий полюс функції
,
тоді вона має такий ряд Лорана :
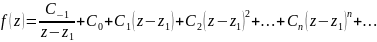 Помножимо обидві частини рівності на
(
Помножимо обидві частини рівності на
( ):
):
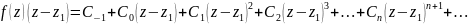 Перейдемо до границі при
Перейдемо до границі при
 :
:
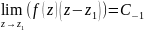 .
.
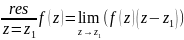 (2). (
(2). ( )
Нехай
функція
)
Нехай
функція
 ,
при чому
,
при чому
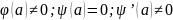 .
В
точці z=a
маємо полюс першого порядку, тоді можемо
записати :
.
В
точці z=a
маємо полюс першого порядку, тоді можемо
записати :
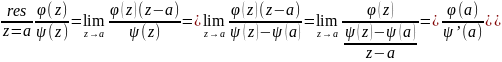 ;
;
 (3);2)Нехай
z=a
– полюс “n”-го
порядку , тоді ряд Лорана для
має такий вигляд:
(3);2)Нехай
z=a
– полюс “n”-го
порядку , тоді ряд Лорана для
має такий вигляд:
 помножимо обидві частини на
помножимо обидві частини на
 :
:
 Продиференціюємо (
Продиференціюємо (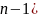 разів і перейдемо до границі при
разів і перейдемо до границі при
 ,
тоді одержимо:
,
тоді одержимо:
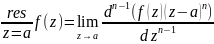 (4)
(4)
12)Лишки
аналітичної функції – озн. Основна
теорема про лишки(без дов).
Лишком аналітичної функції
у нескінченно віддаленій точці
називається коефіцієнт при
в розкладі цієї функції в ряд Лорана,
взятий з протилежним знаком.Теорема.
Нехай
- однозначно аналітична функція в
замкнутій однозначній області
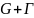 за винятком скінченного числа «n»
особливих точок
за винятком скінченного числа «n»
особливих точок ,
що лежать всередині G.
Тоді має місце рівність :
,
що лежать всередині G.
Тоді має місце рівність :
 (1).
(1).
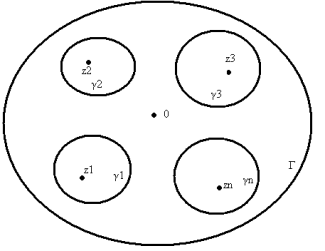 Доведення.
За теоремою Коші для складного контура
Доведення.
За теоремою Коші для складного контура
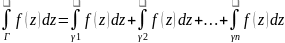 .Помножимо
обидві частини на
.Помножимо
обидві частини на
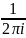 :
:
 .
.
 .Справа
стоїть сума лишків функції
відносно відповідних точок
.Справа
стоїть сума лишків функції
відносно відповідних точок
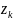 .Зауваження.
Якщо особливих точок немає , то лишки
дорівнюють нулю і ця теорема перетворюється
в теорему Коші.
.Зауваження.
Якщо особливих точок немає , то лишки
дорівнюють нулю і ця теорема перетворюється
в теорему Коші.