5)Обчислення об’єму тіла, обчислення площі фігури, обчислення площі поверхні. Нехай область D обмежена графіками функцій , перетинається прямими паралельно осі не більше , ніж у 2-х точках .Проекція на є правильна область D і обмежена лініями : Тоді можна довести , що потрійний інтеграл обчислюється за формулами : . Отже, обчислення потрійного інтеграла зводиться до послідовного обчислення трьох визначених інтегралів. Якщо перетинається прямими паралельно координатним осям більше ніж у двох точках , то для обчислення потрійного інтегралу треба розділити область Об’єм тіла : . Площа поверхні обчислюється за допомогою поверхневого інтеграла: ; площа фігури обчислюється за допомогою криволінійного інтеграла:

6)Заміна змінних у потрійному інтегралі. Нехай x=x(u,v,w), y=y(u,v,w), z=z(u,v,w), при чому ці функції неперервні і мають неперервні частинні похідні в деякій просторовій області . Вони відображають взаємно однозначно область в області у просторі (u,v,w). Прямокутний паралелепіпед зі сторонами 𝜟x, 𝜟y, 𝜟z відображає деякий криволінійний паралелепіпед, об’єм якого наближено дорівнює об’єму похилого паралелепіпеда. А об’єм останнього обчислюється за допомогою модуля мішаного добутка трьох векторів , на яких цей паралелепіпед побудований.

Можна довести

7) Обчислення потрійних інтегралів у декартових координатах. Нехай область V обмежена поверхнями , , перетинаються прямими паралельними осі oz не більше ніж у двох точках.проекція V на площину xoy є правильна область D,обмежена лініями , , x=a,x=b.тоді можна довести, що потрійний інтеграл обчислюється за формулою . Отже обчислення потрійного інтеграла зводиться до послідовного обчислення трьох визначених інтегралів.

8)Потрійні інтеграли у циліндричних координатах. Положення точки М у циліндричних координатах визначається трьома величинами З маємо 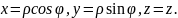Обчислюємо якобіан переходу I: =

Отже,

Зауваження . Якщо область V- циліндр або його частина, то доцільно перейти до циліндричних координат.

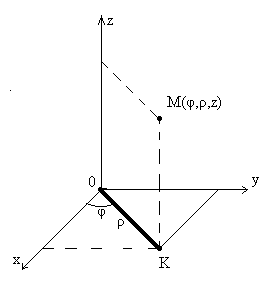
9)Потрійні інтеграли у сферичних координатах. З маємо Отже, Обчислюємо якобіан переходу

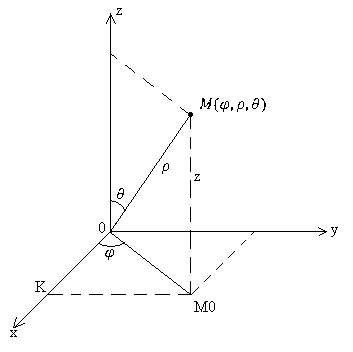
1. 10)Застосування потрійних інтегралів у геометрії та механіці. 1)Обчислення об’єму тіла.Якщо тіло однорідне і густина то об’єм дорівнює :

2. 2)Координати центра мас тіла:

3. 3)Момент інерції тіла відносно координатних осей: