3) После получения классов , , опять строим таблицу переходов и т. Д. До тех пор, пока каждый класс условно эквивалентных состояний, выделенный на предыдущем шаге, не станет неизменным.

Построим таблицу переходов (таблица 3), учитывая разбиение класса .

По таблице 2.1 получим таблицу 3.

Таблица 3

0
1

Анализируя эту таблицу, делаем вывод, что все состояния каждого из выделенных классов переходят под воздействием в один и тот же класс, что обусловливает получение на выходе одного и того же значения для всех состояний класса при одном переходе. Следовательно, все состояния одного класса ведут себя как одно состояние, которым его заменяют.

4) Заменим классы , , соответственно внутренними состояниями , , (таблица 4). В результате получим минимизированный граф переходов (рис. 3, б), задающий то же отображение , что и первоначальный граф переходов (рис. 3, а).

По таблице 1 и таблице 3 построим таблицу 4.

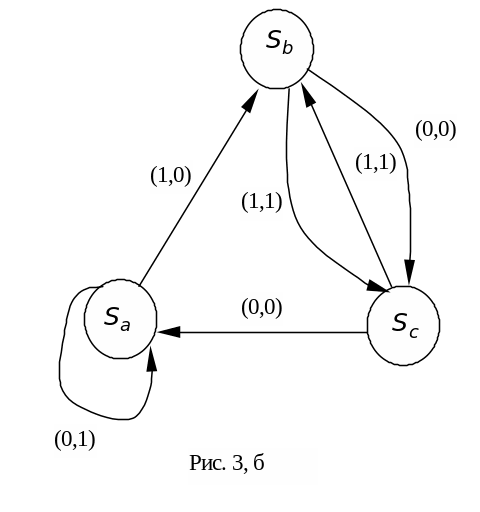
Таблица 4

0
1

Кодирование внутренних состояний

Кодирование производится с целью:

1. сокращения символьного текста при ограниченном количестве кодовых символов – оптимальное кодирование;

2. обнаружения и исправления ошибок при передаче и хранении информации – корректирующее кодирование;

3. защиты информации от несанкционированного доступа – секретное кодирование.

Рассмотрим частотно-матричный метод кодирования состояний. Пусть в результате абстрактного синтеза был построен граф, определяющий отображение . После кодирования получим граф, задающий отображение . Данный метод кодирования реализуем с помощью следующего алгоритма синтеза кодирующего дерева.

1. Строим двумерную матрицу , каждой строке, которой взаимно однозначно соответствует значение входного и выходного каналов (элементы вектора и ), столбцу – внутреннее состояние:

Определение. Множество

называется первичным термом.

Каждому внутреннему состоянию (столбцу матрицы) взаимно однозначно сопоставляем произвольным образом максимальную вершину синтезируемого кодирующего дерева. Полагаем .

2. По матрице находим частотную матрицу отношений

.

3. Вычислим значения производной от графа, используя частотную матрицу отношений .

4. Выбираем пару внутренних состояний, для которой вычисленное значение производной минимально.

5. Выбранную пару состояний вычеркиваем и ставим ей в соответствие в кодирующем дереве вершину, являющуюся началом дуг, концами которых являются выбранные состояния. Построенной вершине взаимно однозначно сопоставляем столбец строящейся матрицы , равный поэлементному произведению столбцов матрицы , соответствующих выбранным вершинам.

6. Проверяем, остались или нет нерассмотренные внутренние состояния, для которых вычислялись значения производной. Если "да", то переходим к п. 4, в противном случае – к п. 7.

7. Проверяем, образована ли матрица . Если да, то полагаем и переходим к п. 2, в противном случае – к п. 8.

8. Каждым двум дугам, исходящим из вершины построенного дерева, начиная с дуг, исходящих из корня дерева, ставим в соответствие 0 и 1.

Путь, соединяющий корень дерева и максимальный элемент, взвешен кодом, который сопоставляется внутреннему состоянию, соответствующему этому максимальному элементу дерева.

9. Конец.

Проиллюстрируем предлагаемый алгоритм на следующем примере.

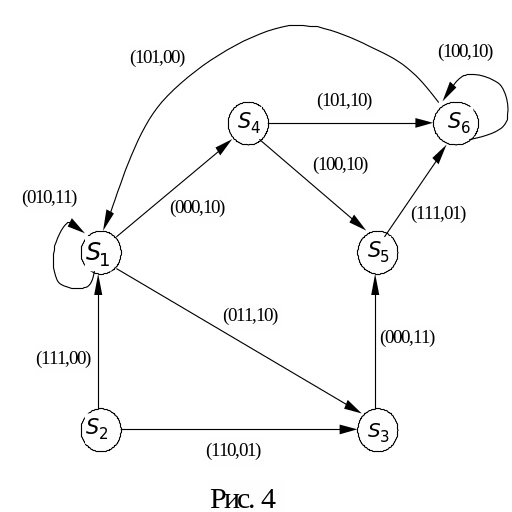
Пример. Пусть в результате абстрактного синтеза был получен граф переходов (рис. 4). Используя рассмотренный алгоритм, закодируем внутренние состояния автомата.

п. 1. Построим матрицу , соответствующую данному графу.

Каждому столбцу матрицы сопоставим максимальную вершину синтезируемого кодирующего дерева.

.

Рисуем верхний ярус дерева (рис. 5)

п. 2. По матрице построим частотную матрицу отношений .

Из определения частотной матрицы отношение следует, что она симметрична относительно главной диагонали, то есть

.

п. 3. Вычисляем значения производной для каждой пары состояний, используя частотную матрицу отношений:

Всего таких пар будет 15 .

.

Остальные значения производной равны .

;

;

;

.

п. 4. Производная 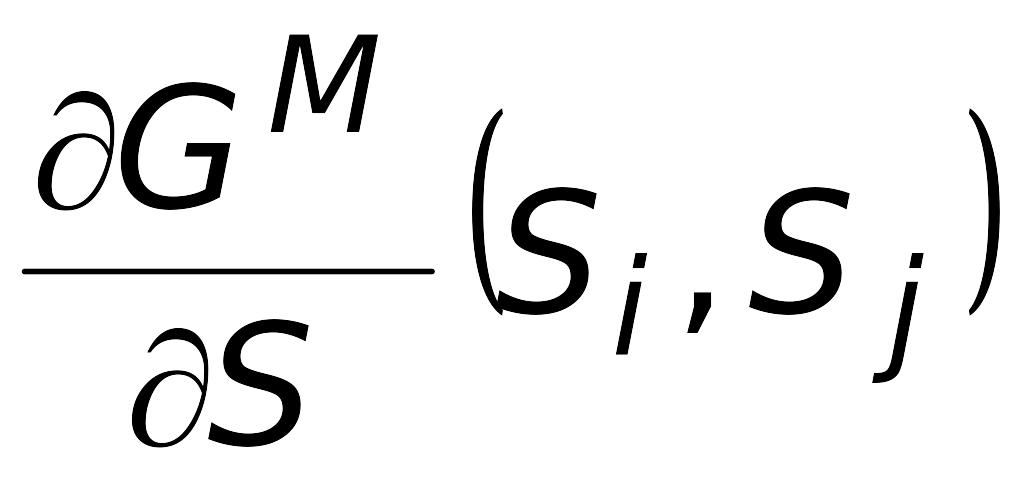имеет минимальное значение на паре .

п. 5. Этой паре состояний ставим в соответствие "пересечение" соответствующих вершин строящегося дерева (рис. 6).

п. 6. и п. 7. Согласно алгоритму, объединяем в пары состояния и , так как значения производной для этих пар состояний минимальны. В результате построим третий ярус дерева (рис. 6).

Элемент матрицы равен поэлементному произведению столбцов матрицы , соответствующих выбранным вершинам.

Матрица , соответствующая вершинам построенного яруса, имеет вид:

.

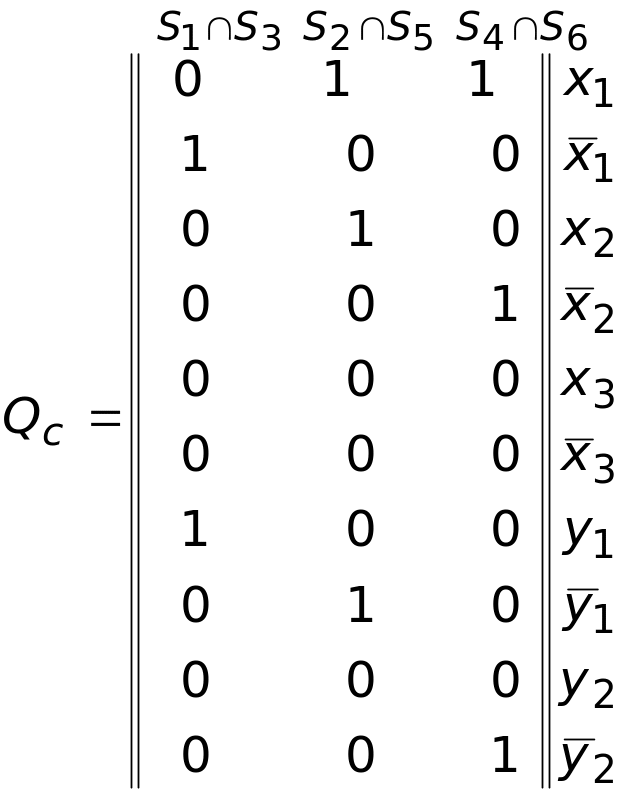Переход к п. 2. Частотная матрица отношений, соответствующая матрице , имеет следующий вид:

.

п. 3. Производная на парах состояний

.

Остальные значения производной равны . Рисуем второй ярус в дереве (рис. 6).

п. 8. Искомое кодирующее дерево изображено на рис. 6. Согласно построенному кодирующему дереву, имеем следующие коды внутренних

состояний автомата: .