4. Определить сходимость числового ряда .

Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся теоремой первым признаком сравнения. Все члены исходного ряда больше соответствующих членов ряда , члены которого образуют геометрическую прогрессию со знаменателем . В примере 7.1.1 было показано, что такие числовые ряды ( ) сходятся. Более того, сумма этого ряда равна  и, следовательно, сумма первоначального ряда не больше чем .►

Теорема (Второй признак сравнения числовых рядов). Пусть члены ряда (108) не меньше соответствующих членов ряда (109), т.е. при n=1, 2, ...

                                                              .                                                                  (111)

Тогда, если ряд (109) расходится, то расходится и ряд (108).

5. Определить сходимость числового ряда .

Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся вторым признаком сравнения. Так как , то члены данного ряда больше соответствующих членов гармонического ряда , который расходится (см. пример 7.1.3). Поэтому исходный числовой ряд также расходится. ►

Теорема (Признак сходимости Даламбера).Пусть дан числовой ряд (97) с положительными членами. Если отношение (n+1)-го члена к n-му члену при  имеет конечный предел, т.е.

                                                         ,                                                               (112)

то       1) при <1 – ряд сходится;

  2) при >1 – ряд расходится.

Замечание. Ряд будет расходиться и в том случае, когда . Это следует из того, что если , то, начиная с некоторого номера n=N, будет иметь место неравенство: >1. Следовательно, > .

6. Исследовать сходимость ряда

Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение , , . Вычисляя предел, получим

<1.

Таким образом, исходный ряд сходится. ►

7. Исследовать сходимость ряда .

Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение , , . Вычисляя предел, получим

 > 1.

Таким образом, исходный ряд расходится. ►

Признак Даламбера дает ответ на вопрос о том сходится ли данный положительный ряд в случае, когда  существует и отличен от 1. Если же этот предел не существует или , то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться или сходящимся, или расходящимся. Для решения вопроса о сходимости надо применить какой-либо другой признак.

Если , но отношение  для всех номеров n, начиная с некоторого больше 1, то ряд расходится. Это следует из того, что если >1, то  >  и общий член ряда не стремится к 0 при n.

8. Исследовать сходимость ряда .

Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим предел отношения

.

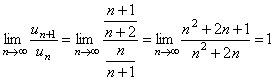В данном случае ряд расходится, так как >1 для всех n. Действительно,

>1   >  1>0. ►