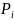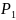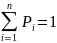1. Классификация событий.

Событие - опытом или испытанием наз. осуществление определенного комплекта условий или действий, при котором происходит соответствующее явление. Возможным результатом опыта наз. событие.

Событие наз.достоверным если оно обязательно произойдет в данном опыте.

Событие наз.невозможным если оно не может произойти в этом опыте.

Событие наз.случайным если оно может произойти, а может и не произойти в этом опыте.

Два события наз. Совместными в данном опыте , если появление одного из них не исключает появление другого в данном опыте.

Два события наз. Несовместными если они не могут произойти вместе при одном и том же испытании.( попадание и промах при одном выстреле-несовместные события). Несколько событий наз несовместными если они попарно несовместимы.

Два события наз. Противоположными , если появление одного из них равносильно непоявлению одного из них равносильно непоявлению из них.( как в учебнике : Противоположными наз. Два единственно возможных события , образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать как А с черточкой над буквой ( не А).

События наз. Равновозможными если есть основания считать что ни одно из них не является более возможным чем другое.

Несколько событий образуют полную группу событий, если в результате испытания появится хотя бы одно из них.

3. 2) Классическое определение вероятности, свойства вероятности.

4. Вероятностью события наз. Отношение числа элементарных исходов, благоприятствующих данному событию ,числу всех равновозможных исходов опыта в которых может появиться это событие.

P-вероятность А-событие m-число элементарных исходов, благоприятствующих событию А. n-число всех равновозможных элементарных исходов опыта, образующих полную группу событий.

Свойства вероятности.

1)Вероятность достоверного события равна 1.D(U)=1

2)Вероятность невозможного события равна 0. P(V)=0

3)Вероятность случайного события выражается положительным числом меньше 1. 0<P(A)<1

4) Вероятность любого события В удовлетворяет неравенством 0≤P(B)≤1

3. Размещение .Сочетание. Перестановки.

Размещением из n элементов по m наз. Любое упорядоченное подмножество из m элементов множества, состоящие из n различных элементов.

Размещение отличается порядком входящих в них элементов и составом. Число размещений из n по m обозначается 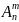m≤n и вычисляется по формуле

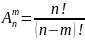
Перестановкой из n элементов наз. Любое упорядоченное множество, в которое входит по одному разу все n размещенных элементов множества , обозначается 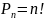.Это один из случаев размещения при котором при n=m.

Сочетанием из n элементов по m наз. Любое подмножество из m элементов, которое принадлежит множеству , состоящему из n различных элементов. Обозначается число сочетаний из n разных элементов по m

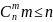
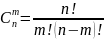
Размещение и сочетание различаются тем что в размещении учитывается порядок, входящих в него элементов, а в сочетании не учитывается.

3. 4) Определение факториала.

Факториал-Произведение всех натуральных чисел до n включительно.

n!=1∙2∙3∙…∙n

0!=1

5)Относительная частота события.

Сопоставляя определения вероятности и относительной частоты , заключаем : определение вероятности не требует , чтобы испытания производились в действительности, Определение же относительной частоты предполагает, что испытания ыли произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту до опыта.

Относительной частотой события или частотой наз . отношение числа опытов ,в котором появилось это событие к числу всех произведенных опытов.

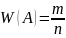W(A) частота

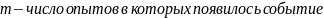
n-число всех произведенных опытов.

6) Геометрическая вероятность.

Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты для которых множество таких исходов бесконечно. Для того, чтобы преодолеть недостаток классического определения вероятности , состоящей в том, что оно не применимо к испытаниям с бесконечным числом исходов водят геометрическую вероятность- это вероятность попадания точки в область.

А-попадания брошенной точки в область g , тогда геометрическая вероятность этого события определяется формулой:

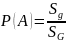для плоскости

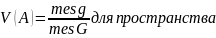
11. 7) Объединение , пересечение, разность 2х событий. Свойства операций пересечения и объединения.

Суммой или объединением 2 событий наз. Событие , состоящее в появлении хотя бы одного из них. Обозначает А U B или А+В.

Произведением или пересечением 2х событий наз. Событие состоящее в одновременном их появлении и обозначается A Л B или A∙B

Разностью событий А и В называется событие С, которое означает, что наступает событие А и не происходит событие В. Обозначается А\ В

Свойства :

1)Свойство коммутативности:

А U B= В U А , А Л В = В Л А

2) Свойство ассоциативности.

(AUB)UC= AU(BUC)=(AUC)UB=AUBUC

(АЛВ)ЛС=АЛ(ВЛС)=(АЛС)ЛВ=АЛВЛС

3)Свойство дистрибутивности

АU(BЛC)=AUB Л AUC

AЛ(BUC)=A Л B U A Л C

6. 8) Теорема сложения и умножения вероятностей двух событий.

Теорема сложения вероятностей двух событий: Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А + В) = Р(А) + Р(В) - Р(АВ) .

Теорема сложения вероятностей двух несовместных событий : Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А + В) = Р(А) + Р(В) (когда А

и В - несовместные события; в этом случае АВ - невозможное событие и Р(АВ) = о.)

Теорема сложения вероятностей n несовместных событий :Вероятность суммы n несовместных событий A1, А2 ••••• Аn равна сумме вероятностей этих событий:

Сумма вероятностей событий А1 • А2 •...• Аn , образующих полную группу, равна единице:

Сумма вероятностей противоположных событий равна единице:

Если обозначить

то формула примет вид p+q=l.

Вероятность события В при условии, что произошло событие А, называется условной вероятностью события В и обозначается так:

Теорема умножения вероятностей : Вероятность nроизведенuя двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло: Событие В не зависит от события А, если

Т.е. вероятность события В не зависит от того, произошло ли событие А. В этом случае и собьпие А не зависит от события В, Т.е. свойство независимости событий является взаимным. если А и В не зависимы, то независимы .

Теорема умножения вероятностей двух независимых событий : Вероятность nроизведенuя двух незавuсuмых событий равна произведению их вероятностей:

Теорема умножения вероятностей n событий: Вероятность nроизведенuя n событий равна nроизведенuю одного из них на условные вероятности всех остальных,. вычисленные в nред- положении, что все предыдущие события наступили:

В частности, для трех событий А, В, С формула принимает вид Р(АВС) = Р(А)Р(В / А)Р(С / АВ)

События A1, А2 , .•• , Аn называются независимыlми в совокупности,или незавиcuмыми, если они попарно-независимы, а также независимы каждое из них и произведение k остальных (k = 2, 3, ... , n-l). Из попарной независимости событий не следует их независимость в совокупности. Если события A1, А2 , ••. , Аn независимы, то противоположные им события также независимы.

Теорема умножения вероятностей n независимых событий : Если события А1 А2 , ••• , Аn незавuсuмы, то вероятность их nроuзведения равна nроuзведению вероятностей этих событий: Равенство выражает необходимое и достаточное условие независимости событий A1, А2 , .•• , Аn . Для трех независимых событий А, В, С формула принимает вид Р(АВС) = Р(А)Р(В)Р(С).

Вычисление вероятности суммы событий можно. свести к вычислению вероятности про изведения противоположных событий по формуле

В частности, если события A1 , А2 , ••• , А, независимы, то или

Если независимые события Ар А2 , ••• , Аn имеют одинаковую вероятость, равную р, то вероятность появления хотя бы одного из этих событий выражается формулой

где А = А1 + А2 + ... + Аn

В обратной задаче вероятность Р(А) известна и нужно определить, при каком числе n независимых событий А; достигается заданное значение Р(А). Точнее говоря, задается некоторое число Q такое, что

из этого неравенства определяется 'значение n.

7. 9) Формула полной вероятности, формулировка

8. Рассмотрим n попарно несовместных событий Н1 Н2 . . . , Hn для

9. которых известны вероятности 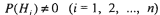и событие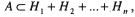 , причем известны условные вероятности Р(А / Нi) . Вероятность события А определяется формулой

10. 

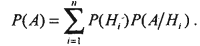
11. эта формула называется формулой полной вероятности. События

12. Н1 Н2 . . . , Hn иногда называют гиnотезамu.

14. 10) Формула Бейеса

Пусть Н1 Н2 , ... , Нn - попарно-несовместные события, вероятности которых Р(Нi О (i = 1,2,... , n), и событие А Н1 + Н2 + .. . + Hn для которого известны условные вероятности Р(А/ Нi) (i = 1,2, .. . , n). Произведен опыт, в результате которого появилось событие А . Условные вероятности событий Н1 Н2 , ... , Нn относительно события А определяются формулами

или где

- формула полной вероятности

7. 11) Закон распределения дискретной случайной величины

Величина называется случайной , если она может принимать то или иное значение с некоторой вероятностью.

Случайная величина называется дискретной , если она принимает конечное и счетное число значение.

Случайная величина называется непрерывной, если она может принимать любое значение из некоторого промежутка (конечного или бесконечного).

Законом распределения случайной величины , называется правило, (формула, таблица, график) по которому определяется вероятность для каждого значения случайной величины.

ξ – случайная величина кси

Ряд распределения

ξ =

=
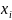
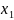