30. Нормальный алгоритм Маркова.

Нормальные алгорифмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах.

Определение всякого нормального алгорифма состоит из двух частей: определения алфавита алгорифма (к словам из символов которого алгорифм будет применяться) и определения его схемы. Схемой нормального алгорифма называется конечный упорядоченный набор так называемых формул подстановки, каждая из которых может бытьпростой или заключительной. Простыми формулами подстановки называются слова вида  , где L и D — два произвольных слова в алфавите алгорифма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида  , где L и D — два произвольных слова в алфавите алгорифма. При этом предполагается, что вспомогательные буквы   и   не принадлежат алфавиту алгорифма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгорифма в пятибуквенном алфавите | * abc может служить схема

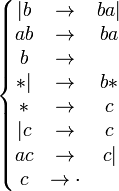
Процесс применения нормального алгорифма к произвольному слову V в алфавите этого алгорифма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем. Пусть V' — слово, полученное на предыдущем шаге работы алгорифма (или исходное слово V, если текущий шаг является первым). Если среди формул подстановки нет такой, левая часть которой входила бы в V', то работа алгорифма считается завершённой, и результатом этой работы считается слово V'. Иначе среди формул подстановки, левая часть которых входит в V', выбирается самая первая. Если эта формула подстановки имеет вид  , то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего работа алгорифма считается завершённой с результатом RDS. Если же эта формула подстановки имеет вид  , то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего словоRDS считается результатом текущего шага, подлежащим дальнейшей переработке на следующем шаге.

Например, в ходе процесса применения алгорифма с указанной выше схемой к слову | * | | последовательно возникают слова | b * | , ba | * | , a | * | , a | b * , aba | * , baa | * , aa | *, aa | c, aac, ac | и c | | , после чего алгорифм завершает работу с результатом | | . Другие примеры смотрите ниже.

31. Машина Тьюринга. Описание, пример.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_jзаписывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <q_i, a_j> имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.