28. Примитивно – рекурсивные и частично – рекурсивные функции. Пример построения рекурсивной функции.

Определение 8.5. Частично рекурсивные функции. Функция f называется частично рекурсивной функцией (ч.р.ф.), если она является одной из простейших функций или может получиться из них с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии иминимизации, т.е. существует последовательность функций f₁,f₂,..., f_n=f, каждая из которых является либо простейшей, либо получена из предыдуших с помощью одного из указанных операторов. Указанная последовательность функций называется частично рекурсивным описанием функции f.Функция f называется общерекурсивной функцией (о.р.ф.), если она частично рекурсивна и всюду определена.Функция f называется примитивно рекурсивной функцией (п.р.ф.), если она частично рекурсивна и для нее существует частично рекурсивное описание, использующее лишь операторы суперпозиции и примитивной рекурсии. В таком случае оно называется примитивно рекурсивным описанием функции f.Нетрудно проверить, что каждая примитивно рекурсивная функция всюду определена, т.е. является общерекурсивной (обратное, вообще говоря, неверно).

Примеры Приведем некоторые примеры частично рекурсивных функций.

Пример 8.1. Постоянные функции. Пусть fⁿ(x₁,...,x_n)=k для всех наборов аргументов (x₁,...,x_n) и числа  . Тогда

Пример 8.2. Сложение: +²(x,y)=x+y. Функция сложения определяется следующей примитивной рекурсией.

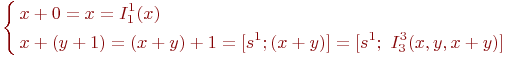
Следовательно, +² =R(I₁¹,[s¹;I₃³]).

Пример 8.3. Умножение: x²(x,y)=x x y.

Используя сложение, умножение можно задать следующей примитивной рекурсией:

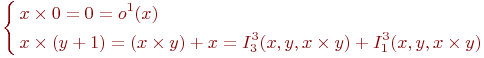
Следовательно, x² =R(o¹,[+;I₃³,I₁³]).

Пример 8.4. Минус 1:  .

Нетрудно проверить, что  .

Пример 8.5. Вычитание :  , если x >= y и  , если x < y.

Вычитание определяется следующей примитивно рекурсивной схемой:

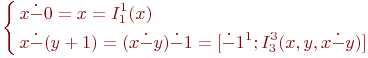
Следовательно,  .

29. Эквивалентность слов в ассоциативном исчислении. Определения, пример.

Пусть A - ас­со­ци­атив­ное ис­чис­ле­ние в ал­фа­ви­те , опре­де­ля­емое сис­те­мой со­от­но­ше­ний S.

Обоз­на­чим |^A - би­нар­ное от­но­ше­ние, опре­де­лён­ное на мно­же­ст­ве ^*, и на­зо­вём его от­но­ше­ни­ем смеж­но­сти слов.

 

Опре­де­ле­ние (по [Мар­ков,Нагорный,1996,с.308]).

Бу­дем го­во­рить, что сло­во  смеж­но со сло­вом  в ас­со­ци­атив­ном ис­чис­ле­нии A (и обоз­на­чать этот факт |^A), ес­ли сло­во  мо­жет быть по­лу­че­но из сло­ва  в ре­зу­ль­та­те ров­но од­но­го дей­ст­вия, до­пус­ти­мо­го от­но­си­те­ль­но S, т.е. най­дё­т­ся та­кое со­от­но­ше­ние ₁₂ в ал­фа­ви­те  и та­кие сло­ва ,^*, что ли­боReplace(,*₁*,₂)=, ли­бо

Replace(,*₂*,₁)=.

Пусть , ₁,₂,...,_n^*.

 

Опре­де­ле­ние.

(1) -сис­те­мой слов в ал­фа­ви­те  на­зо­вём сло­во ₁₂..._n.

(2) Бу­дем го­во­рить, что сло­во ₁ со­сед­ст­ву­ет сле­ва со сло­вом ₂ в -сис­те­ме слов, ес­ли сло­во ₁₂ яв­ля­ет­ся под­сло­вом -сис­те­мы слов в ал­фа­ви­те .

(3) (По [Мар­ков,Нагорный,1996,с.308]) A-ря­дом на­зо­вём та­кую -сис­те­му слов в ал­фа­ви­те , что ес­ли вся­кий раз, ког­да сло­во ₁ со­сед­ст­ву­ет сле­ва со сло­вом ₂ в-сис­те­ме слов, то ₁|^A₂.

(4) (По [Мар­ков,Нагорный,1996,с.308]) A-ря­дом, со­еди­ня­ющим сло­во ₁ со сло­вом _n на­зо­вём A-ряд ви­да ₁₂..._n.

 

Пусть ,^*. Обоз­на­чим |^A - би­нар­ное от­но­ше­ние, опре­де­лён­ное на мно­же­ст­ве ^*, и на­зо­вём его от­но­ше­ни­ем эк­ви­ва­ле­нт­но­сти слов.

 

Опре­де­ле­ние [Мар­ков,Нагорный,1996,с.308].

Бу­дем го­во­рить, что сло­во  эк­ви­ва­ле­нт­но сло­ву  в ас­со­ци­атив­ном ис­чис­ле­нии A (и пи­сать: |^A), ес­ли мо­жет быть по­стро­ен A-ряд, со­еди­ня­ющий сло­во  со сло­вом.

 

Для двух кон­крет­ных слов  и  в ал­фа­ви­те ас­со­ци­атив­но­го ис­чис­ле­ния A мо­жет быть по­став­ле­на сле­ду­ющая важ­ная за­да­ча: "Вер­но ли, что |^A?". Дан­ная за­да­ча на­зы­ва­ет­ся еди­нич­ной про­бле­мой рас­по­зна­ва­ния эк­ви­ва­ле­нт­но­сти слов  и  в ас­со­ци­атив­ном ис­чис­ле­нии A. Яс­но, что вся­ко­му ас­со­ци­атив­но­му ис­чис­ле­нию A со­от­ве­т­ст­ву­ет класс по­до­бных еди­нич­ных про­блем.

Про­бле­мой эк­ви­ва­ле­нт­но­сти для ас­со­ци­атив­но­го ис­чис­ле­ния A на­зы­ва­ет­ся сле­ду­ющая мас­со­вая ал­го­рит­ми­че­с­кая про­бле­ма, со­от­ве­т­ст­ву­ющая это­му клас­су еди­нич­ных про­блем: "Най­ди­те еди­ный ал­го­ритм, по­зво­ля­ющий узна­вать для лю­бых двух дан­ных слов  и , яв­ля­ют­ся ли они эк­ви­ва­ле­нт­ны­ми в ас­со­ци­атив­ном ис­чис­ле­нии A".