15. Конечный автомат. Входной и выходной алфавит, функции переходов и выходов

Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров:  , где:

• Q — конечное множество состояний автомата;

• q₀ — начальное (стартовое) состояние автомата ( );

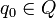• F — множество заключительных (или допускающих) состояний, таких что  ;

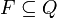• Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;

• δ — заданное отображение множества 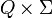  во множество 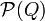  подмножеств Q:

1. Диаграмма состояний (или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого — состояния КА, ребра — переходы из одного состояния в другое, а нагрузка — символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного из нескольких символов, то над дугой диаграммы (ветвью графа) должны быть надписаны все они.

2. Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.

16. Табличное задание автомата. Примеры.

Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.

17. Задание автомата диаграммой Мура. Примеры.

Диаграмма Мура — один из способов задания конечного детерминированного автомата. Диаграмма Мура представляет собой изображенный на плоскости ориентированныйграф, вершины которого взаимно однозначно соответствуют состояниям автомата , а дуги — входным символам.

18. Задание автомата системой булевых функций. Примеры.

19. Элемент задержки и его описание. Диаграмма, таблица.

24. Разрешимый предикат, разрешимое множество, перечислимое множество

такой n-местный предикат Р, заданный на нек-ром множестве конструктивных объектов (напр., натуральных чисел) М, для к-рого существует алгоритм, позволяющий для любого набора а 1; . . ., а п элементов множества Мнайти значение (И или Л) предиката Рна этом наборе. Иными словами, предикат является разрешимым, если он, рассматриваемый как n-местная функция на Мсо значениями во множестве , является вычислимой функцией. Когда в качестве математич. уточнения понятия вычислимости используется понятие рекурсивной функции или какое-либо эквивалентное понятие, то вместо "Р. п." обычно употребляется термин "рекурсивный предикат"

Разрешимое множество в логике, множество, расположенное в некоторой совокупности конструктивных объектов (т. е. множество, составленное из каких-то объектов этой совокупности), для которого существует алгоритм, разрешающий это множество (относительно объемлющей совокупности) в следующем смысле: алгоритм применим к любому объекту объемлющей совокупности и даёт в качестве результата ответ на вопрос, принадлежит ли этот объект к рассматриваемому множеству или нет.

В теории множеств, теории алгоритмов и математической логике, множество натуральных чисел называется разреши́мым или рекурси́вным, если существует алгоритм, который, получив на вход любое натуральное число, через конечное число шагов завершается и определяет, принадлежит ли оно данному множеству. Другими словами, множество является разрешимым, если его характеристическая функция вычислима. Множество, не являющееся разрешимым, называется неразреши́мым

В теории множеств, теории алгоритмов и математической логике, перечисли́мое мно́жество (эффекти́вно перечислимое, рекурси́вно перечислимое,полуразреши́мое множество^[1]) — множество конструктивных объектов (например, натуральных чисел), все элементы которого могут быть получены с помощью некоторогоалгоритма. Дополнение перечислимого множества называется корекурсивно перечислимым.

25. Алгоритм вычисления числа π.

26. Три типа просиейших функций.

Простейшие функции. Функция называется простейшей, если она является одной из следующих функций:

• o¹(x)=0 - тождественный нуль;

• s¹(x)= x+1 - следующее число (плюс один);

• функции выбора аргумента I_mⁿ (x₁, ... ,x_n)=x_m (1 <= m <= n).

Заметим, что все простейшие функции вычислимы в интуитивном смысле. 

27. Операторы суперпозиции, примитивной рекурсии и минимизации.

Суперпозиция. Пусть F^m и f₁ⁿ,..., f_mⁿ - арифметические функции. Скажем, что функцияGⁿ получена из F^m , f₁ⁿ, ..., f_mⁿ с помощью оператора суперпозиции (обозначение: Gⁿ=[F^m;f₁ⁿ, ..., f_mⁿ]), если для всех наборов аргументов (x₁,...,x_n)

При этом для каждого набора аргументов (a₁, ..., a_n) функция   (т.е. определена), если определены все значения f₁ⁿ (a₁, ..., a_n)=b₁,..., f_mⁿ (a₁, ..., a_n)=b_m и  .

Определение 8.2. Примитивная рекурсия. Скажем, что функция Fⁿ⁺¹(x₁,... ,x_n,y) получена с помощью оператора рекурсии из функцийgⁿ(x₁,..., x_n) и hⁿ⁺²(x₁, ..., x_n, y, z), если она может быть задана схемой примитивной рекурсии

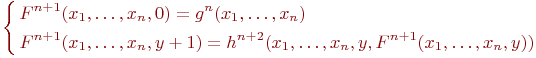
В этом случае будем писать Fⁿ⁺¹ = R(gⁿ,hⁿ⁺²).

При этом   и для каждого b

 и  .

В случае, когда n=0, т.е. F зависит от одного аргумента y, а аргументов x₁,...,x_n нет, схема примитивной рекурсии принимает вид

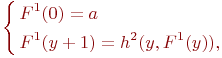
где  .

Заметим, что если исходные функции в операторах суперпозиции и примитивной рекурсии всюду определены, то и результирующие функции также всюду определены. Следующий оператор позволяет задавать не всюду определенные, т.е. частичные, функции.

Определение 8.3. Минимизация. Скажем, что функция Fⁿ(x₁,... ,x_n) получена с помощью оператора минимизации(   -оператора) из функцииgⁿ⁺¹(x₁,..., x_n,y), если Fⁿ(x₁,...,x_n) определена и равна y тогда и только тогда, когда все значения gⁿ⁺¹(x₁,..., x_n,0),...,gⁿ⁺¹(x₁,..., x_n,y-1) определены и не равны 0, а gⁿ⁺¹(x₁,..., x_n,y)=0. В этом случае будем писать