45)Линейная зависимость и линейная независимость векторов. Примеры.

О пределение

С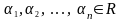 овокупность векторов называется линейно зависимой (ЛЗС),

е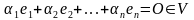 сли найдутся числа , не равные нулю одновременно, такие, что выполняется равенство:

В противном случае совокупность называется линейно независимой (ЛНС).

П окажем, что система столбцов

линейно зависима.

Д ействительно,

О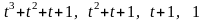 чевидно, что полученная СЛУ имеет нетривиальные решения (например, ).

П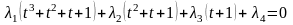 окажем, что система многочленов линейно независима.

Д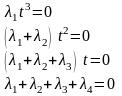 ействительно,

46)Евклидово пространство. Определение и простейшие свойства скалярного пространства.

О пределение.

Д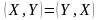 ействительное линейное пространство E называется евклидовым пространством , если каждой паре векторов X и Y из E поставлено в соответствие действительное число , называемое скалярным произведением векторов X и Y, причем выполнены следующие условия:

1 ) ;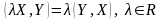

2 ) ;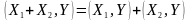

3)

47)Длина вектора. Угол между векторами. Ортогональность векторов.

О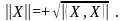 пределение.

Д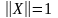 линой вектора X называется число

Если , то вектор X называется нормированным.

А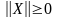 лгебраические свойства длины вектора:

1 ) ;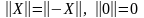

2 ) ;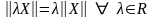

3) .

Угол между векторами.

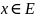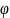     Углом между векторами и называют угол ,для которого ,

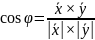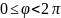
Ортогональные векторы.

Векторы 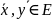ортогональны, если

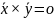
4 8)Скалярное произведение в Rⁿ. Длина вектора и угол между векторами в Rⁿ.

Определение.

Скалярным произведением векторов

н азывается число

С войства скалярного произведения выполнены:

1 ) ;

2 ) ;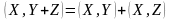

3 ) ;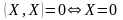

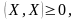4) причем

Д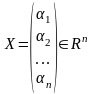 лина вектора.

Определение.

Длиной вектора называется число

Угол между векторами.

Угол между ненулевыми векторами

в пространстве Rⁿ :

У словие ортогональности векторов:

49)Неравенство Коши-Буняковского.

Д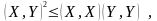 ля любых векторов X и Y евклидова пространства E справедливо неравенство Коши-Буняковского

к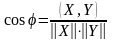 оторое позволяет следующим образом определить угол между ненулевыми векторами:

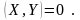
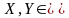
Ненулевые векторы E называются ортогональными, если

50)Построение ортогональго базиса в Rⁿ.

Задача.

П роверить ортогональность системы векторов

и дополнить ее до ортогонального базиса.

Р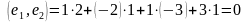 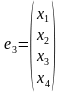ешение.

Д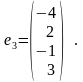 ля определения достаточно найти какое-либо

р 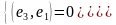ешение системы

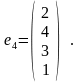
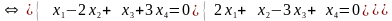
Д 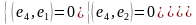ля определения e₄

51) Ортонормированный базис.

О пределение.

Б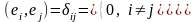 азис n-мерного евклидова пространства называется ортонормированным, если

Другими словами, ортонормированным базисом называется базис, состоящий из попарно ортогональных векторов, каждый из которых имеет длину, равную единице

52)Процесс ортогонализации Шмидта.

Теорема (об ортогонализации)

В любом подпространстве евклидова пространства E

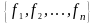можно выбрать ортонормированный базис.

Е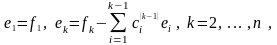 сли задан произвольный базис , то векторы

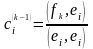
где , образуют ортогональный базис,

а - ортонормированный базис.

53)Ортогональное дополнение подпространства Rⁿ. Определение и свойства.

Определение

О ртогональным дополнением подпространства U из Rⁿ называется подпространство, состоящее из векторов, ортогональных любому вектору из U.

С войства ортогонального дополнения:

5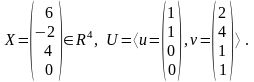 4)Расстояние и угол между вектором и подпространством.

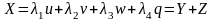
Ортогональная составляющая

Проекция

Д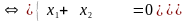 ля нахождения w и q достаточно найти какие-либо два решения системы

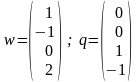
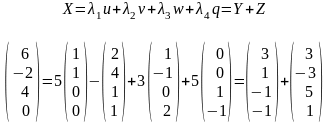
Z

Y

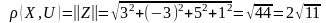
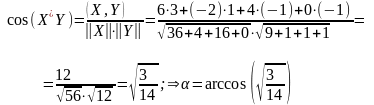
5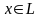 5) Определение линейного оператора. Пример.

Л инейным оператором в линейном пространстве L называется всякое отображение A : L → L пространства в себя, ставящее каждому

е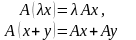 динственный элемент , и обладающее

свойствами

Пример 1.

Я вляется ли отображение A: R³→ R³

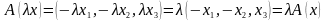— поворот пространства R³ на угол p относительно вектора k=(0,0,1) — линейным оператором?

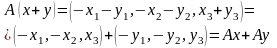
Отображение A является линейным оператором.

Пример 2.

Я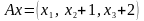 вляется ли отображение A : R³→ R³

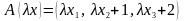л инейным оператором?

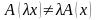
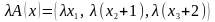
Отображение A не является линейным оператором.

5 6)Матрица линейного оператора. Определение и пример.Пусть A – линейный оператор в конечномерном

пространстве L_n и – некоторый фиксированный базис.

Р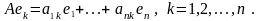 азложим векторы Ae_k по базису B:

Т огда матрица

называется матрицей оператора A в базисе B.

Пример 3.

Оператор A: R³→ R³ поворота пространства R³

на угол p относительно вектора k=(0,0,1)

является линейным оператором.

Е 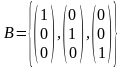го матрица в ортонормированном базисе

имеет вид

Пример 4.

Л инейные операторы A и B действуют в R³

следующим образом:

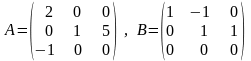для всех x из  R³

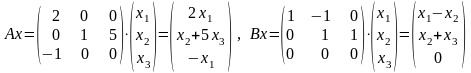
57)Ядро и образ линейного оператора. Определение и пример.

Ядром линейного оператора называется множество элементов из L , образом которых является нулевой элемент.

Я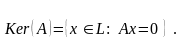 дро оператора обозначают Ker(A) :

 

Ядро линейного оператора - линейное пространство.

Рассмотрим линейный оператор A , действующий в конечномерном линейном пространстве L .

О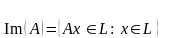 бразом линейного оператора называется

П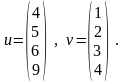 ример(о.п.):

П роверить, принадлежат ли векторы  u и v образу оператора.

Е 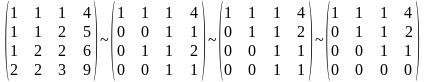сли базисные столбцы матрицы оператора и рассматриваемый вектор образуют линейно зависимую систему, то вектор принадлежит Im(A). В противном случае вектор не прина-длежит Im(A) .

1.

В 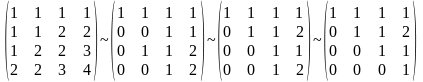ектор u принадлежит Im(A) .

2.

Вектор v не принадлежит Im(A) .

П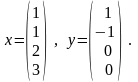 ример(я.о):

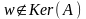
П роверить, принадлежат ли векторы  x и y ядру оператора A.

Е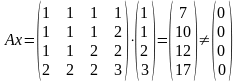 сли для рассматриваемого вектора w Aw=O ,то . В противном случае

1.

В ектор x не принадлежит Ker(A) .

2.

Вектор y принадлежит Ker(A) .

58)Преобразование матрицы линейного оператора при преобразовании базиса.

О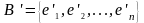 пределение.

М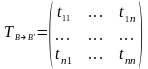 атрицей перехода от базиса к базису называется матрица

,

k-й столбец которой есть столбец координат вектора в базисе B.

59)Приведение матрицы оператора к диагональному виду.

Пусть A и A’ – матрицы оператора A в базисахB и B’, а T = T_B→B’ – матрица перехода от базисаB к базису B’.

Т огда формула преобразования матрицы оператора при преобразовании базиса имеет вид

Если оператор A, действующий в пространстве L_n , имеет n линейно независимых собственных векторов e₁, e₂, … , e_n , соответствующих собственным числам

λ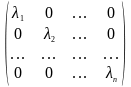 ₁, λ₂, … , λ_n , то в базисе из этих векторов матрица оператора A имеет диагональный вид

60)Квадратичная формула. Определение и пример.

К вадратичной формой называется однородный многочлен второй степени от нескольких переменных над полем вещественных чисел.

П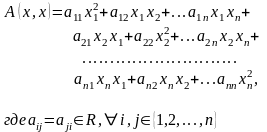 усть - переменные. Тогда

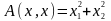
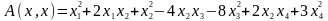- квадратичная форма в R².

- квадратичная форма в R⁴.

61)Матрица квадратичной формы. Определение и пример.

М атричной записью квадратичной формы называется следующее выражение:

6 2)Канонический и нормальный вид квадратичной формы. Определение и пример.

П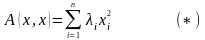 усть в некотором базисе выражение квадратичной формы не содержит произведений , т.е.

Т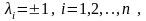 огда выражение (*) называется каноническим видом квадратичной формы.

В частности, если

то получаем нормальный вид квадратичной формы.

63) Методы приведения квадратичной формы к каноническому виду. Идея метода Лагранжа. Пример.

Любую вещественную квадратичную форму невырожденным линейным преобразованием переменных можно привести к диагональному виду, т.е. преобразованная квадратичная форма состоит только из квадратов новых переменных с некоторыми коэффициентами.

Пример:

К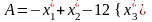 вадратичная форма принимает канонический(диагональный) вид

П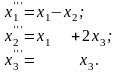 ри этом

64) Методы приведения квадратичной формы к каноническому виду. Идея метода собственных векторов. Пример.

65) Теоремы об ортогональном преобразовании вещественных квадратичных форм.

Л 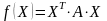юбую вещественную квадратичную форму можно привести к диагональному виду при помощи линейного преобразования переменных с ортогональной матрицей.

П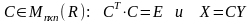 усть , где

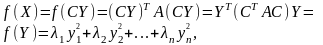Т огда существует

где – собственные числа матрицы А, а столбцы матрицы С – собственные векторы,