1)Матрицы. Сложение матриц. Умножение матрицы на число.

О пределение

М атрицей размера m х n называется прямоугольная таблица из чисел (элементов матрицы),

Обозначения

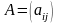
Суммой A+B матриц размера mхn и называется матрица того же размера,

к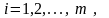 аждый элемент которой равен сумме соответственных элементов матриц A и B :

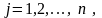
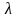
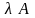
П роизведением числа и матрицы

н азывается матрица , получающаяся из матрицы A умножением всех ее элементов на :

2 )Умножение матриц. Определение и свойства.

П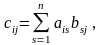 роизведением AB матрицы размера mхn и матрицы размера nхk называется матрица размера mхk , элемент которой равен сумме произведений соответственных элементов i-ой строки матрицы A и j-го столбца матрицы B :

1. A(B+C) = AB + AC

2. (A+B)C = AC + BC

3. λ(AB)=(λA)B=A(λB)

4. А(ВС)=(АВ)С

3)Некоммутативность умножения матриц. Примеры.

Д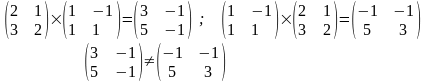 ля матриц, вообще говоря, АВ ≠ ВА

Пример:

Если АВ = ВА, матрицы А и В называются коммутирующими.

4)Единичная матрица. Свойства.

Д ля квадратных матриц определена единичная матрица порядка n – квадратная матрица nxn , все диагональные элементы которой равны единице, а остальные – нулю:

Для любой квадратной матрицы А выполнено:

АЕ = ЕА = А

5 )Транспонированная матрица. Свойства.

A - матрица размера m x n

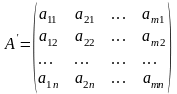
- матрица размера n x m ,называется транспонированной для A

О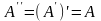 бозначения:

Н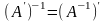 екоторые свойства:

6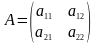 )Определители 2-го и 3-го порядка.

О

+

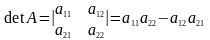пределителем 2-го порядка, соответствующим матрице A (определителем матрицы А),называется число

-

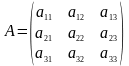
О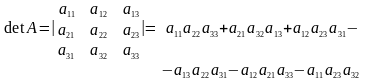 пределителем 3-го порядка, соответствующим матрице A , называется число

П

-

равило Саррюса

1

-

+

+

2

-

+

3

1

2

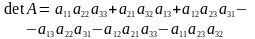
7 )Определение определителя n-го порядка.

О пределителем n-го порядка, соответствующим матрице A, называется число detA, равное сумме всех произведений элементов матрицы, взятых по одному из каждого столбца и каждой строки и снабженных знаком «+» или «-» по определённому правилу – «правилу знаков».

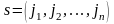
Число t (s) равно числу транспозиций, которое нужно сделать, чтобы перейти от основной перестановки (1,2,…,n) к перестановке

8)Свойства определителя.

1.Умножение некоторой строки (столбца) матрицы определителя на некий коэффициент равносильно умножению самого определителя на этот коэффициент.

Е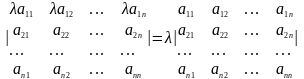 сли все элементы некоторой строки (столбца) содержат общий множитель, то его можно вынести за знак определителя).

2.Если все элементы некоторой строки (столбца) матрицы равны нулю, то и определитель равен нулю.

3.При перестановке двух строк (столбцов) между собой величина определителя меняет лишь знак.

4.Определитель не меняется при транспонировании (свойство равноправности строк и столбцов матрицы).

5.Определитель с двумя одинаковыми строками (столбцами) равен нулю.

6.Определитель с двумя пропорциональными строками (столбцами) равен нулю.

7.Если в определителе некоторая строка (столбец) есть сумма двух других строк (столбцов), то определитель равен сумме двух определителей с этими строками (столбцами) , а все остальные строки (столбцы) этих определителей равны строкам (столбцам) исходного определителя.

8.Если к некоторой строке (столбцу) определителя прибавить другую строку (столбец), умноженную на произвольное число, то величина определителя не изменится.

9 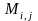)Минор. Связь между минором и алгебраическим дополнением матрицы.

М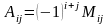 инором соответствующим элементу определителя n-го порядка, называется определитель (n-1)-го порядка, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.

Справедливо следующее равенство

1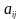 0)Алгебраическое дополнение элемента матрицы. Разложение определителя по строке(столбцу).

А лгебраическим дополнением элемента называется следующий определитель n-го порядка

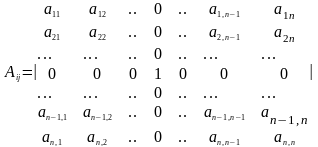
i-ая строка

j-й столбец

Разложение определителя

    

 По элементам i-й строки:

По элементам j-го столбца:

11)Определитель верхнетреугольной матрицы. Примеры

О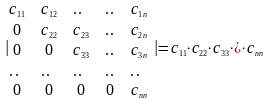 пределитель верхнетреугольной матрицы равен произведению элементов главной диагонали.

12)Определитель клеточно-диагональной матрицы. Примеры.

О пределитель клеточно-диагональной матрицы равен произведению определителей матриц, являющихся клетками исходной матрицы.

А=

13) Метод элементарных преобразований

Матрица определителя приводится элементарными преобразованиями над строками (или столбцами) к верхнетреугольному виду.

О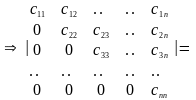 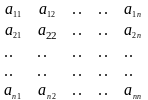пределитель полученной матрицы вычисляется как произведение диагональных элементов:

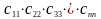
1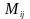 4)Метод понижения порядка

М инором соответствующим элементу определителя n-го порядка, называется определитель (n-1)-го порядка, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.

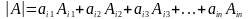С праведливо следующее равенство

Разложение определителя по i-ой строке

15)Метод рекуррентных соотношений

Метод позволяет выразить данный определитель, преобразуя его (например, разлагая по строке или столбцу), через определитель того же вида, но более низкого порядка

17)Определитель Вандермонда.

П окажем, что при любом n (n≥2) определитель Вандермонда равен произведению всевозможных разностей вида

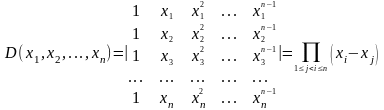
18)Обратная матрица. Определение и простейшие свойства.

Квадратная матрица А называется обратимой, если найдётся квадратная матрица В такая, что выполняются равенства:

А ^. В = В ^. А = Е

В этом случае матрица В называется обратной к матрице А и обозначается

В = А^-1

Е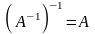 сли квадратные матрицы А и В обратимы, то справедливы следующие соотношения

Доказательство:

19)Теорема об условии существования обратной матрицы

Д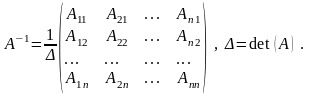 ля того чтобы для матрицы А существовала обратная, необходимо и достаточно, чтобы определитель матрицы был отличен от нуля, т.е. чтобы А была невырожденной. При этом

2 1) Методы построения обратной матрицы: метод присоединенной матрицы

П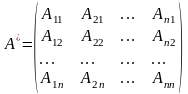 рисоединенная матрица определяется как транспонированная к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы A :

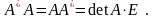
С праведливо равенство

Из теоремы следует, что если A – невырожденная матрица, то

20) Методы построения обратной матрицы: метод элементарных преобразований

Элементарные преобразования матрицы:

1. перестановка строк (столбцов);

2. умножение строки (столбца) на число, отличное от нуля;

3. прибавление к элементам строки (столбца) элементов другой строки (столбца), умноженных на некоторое число.

Для данной квадратной матрицы A n-го порядка строят прямоугольную матрицу Г_А = ( A | E ) размера nх2n, приписывая к A справа единичную матрицу.

Используя элементарные преобразования над строками, приводят матрицу Г_А к виду ( E | B ) , что всегда возможно, если A невырождена. Тогда B = A^-1.

2 2) Под системой линейных уравнений (СЛУ) будем понимать:

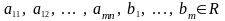
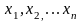
где – «неизвестные» системы , - коэффициенты системы, m – число уравнений, n – число неизвестных.

Р ешение СЛУ

Р ешением СЛУ называется совокупность чисел ,удовлетворяющая всем уравнениям системы, т.е. обращающая их в верные числовые равенства:

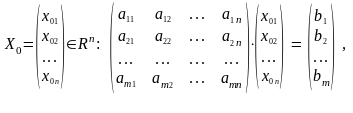
Матричная запись решения СЛУ

23)Равносильные СЛУ. Совместные СЛУ. Примеры

СЛУ называется совместной, если у неё имеется хотя бы одно решение, в противном случае СЛУ называется несовместной.

Две системы называются равносильными, если их множества решений совпадают.

24)Ранг матрицы. Определение и основные свойства

Рангом rgA матрицы А = {a_ij} называется целое число r , такое, что среди миноров r–го порядка матрицы А имеется хотя бы один, отличный от нуля,

а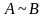 все миноры (r+1)-го порядка равны нулю или миноров порядка (r+1) вообще нет.

В ведём обозначение для матриц, полученных друг из друга элементарными преобразованиями.

Теорема (об инвариантности ранга при элементарных преобразованиях): если , то rgA = rgB ё

2 5) Вычисление ранга матрицы. Метод элементарных преобразований.

М етод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования, матрицу можно привести к трапециевидному виду, т.е. такому виду, когда все элементы при равны нулю и все строки с номерами i > r являются нулевыми.

Тогда rgA = r

26) Вычисление ранга матрицы. Метод окаймляющих миноров.

Пусть в матрице найден минор M k-го порядка, отличный от нуля. Рассматривают те миноры (k+1)-го порядка, которые содержат в себе (окаймляют) минор M. Если все они равны нулю, то rgA = k.

В противном случае среди окаймляющих миноров найдется ненулевой минор (k+1)-го порядка, и вся процедура повторяется.

27)Теорема Кронекера-Капелли

С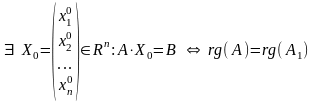 ЛУ совместна (т.е. имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы коэффициентов равен рангу расширенной матрицы системы:

28)Теорема о числе решений СЛУ.

Пусть дана совместная СЛУ от n неизвестных с матрицей коэффициентов ранга r .

Тогда:

1. если r = n , то система имеет единственно решение;

2. если r < n , то система имеет бесконечно много решений, причем (n – r) неизвестным можно присвоить произвольные значения, а остальные r неизвестных выражаются через них единственным образом.

29)Правило Краммера для решения СЛУ.

П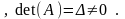 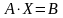усть дана совместная СЛУ от n неизвестных

Т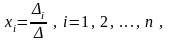 огда система имеет единственное решение

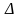
где – определитель, получаемый из определителя заменой i -го столбца на столбец свободных членов.

30)Метод Гаусса решения СЛУ

Метод Гаусса заключается в приведении расширенной матрицы СЛУ элементарными преобразованиями над строками к некоторому специальному виду (треугольному для матрицы коэффициентов) – прямой ход схемы Гаусса и нахождению затем множества решения системы с полученной расширенной матрицей (эта система равносильна исходной) – обратный ход схемы Гаусса.

31)Метод обратной матрицы решения СЛУ

П усть дана совместная СЛАУ от n неизвестных

Т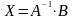 огда существует A^-1 и

,т.е.

3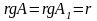 2)Алгоритм решения СЛУ произвольного вида. Общее решение СЛУ.

П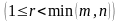 усть , т.е. система совместна,

Приведем матрицу A к трапециевидному виду.

О тбросив последние m – r уравнений, запишем укороченную систему, эквивалентную исходной:

Для каждого набора свободных неизвестных

x_r+1= с₁ , x_r+2= с₂ , … , x_n= с_n-r

у короченная система имеет единственное решение:

называемое общим решением исходной СЛУ.

33) Однородная система A^.X=0 всегда совместна, т.к. имеет тривиальное решение X=0.

Для существования нетривиального решения однородной системы необходимо и достаточно, чтобы выполнялось r = rgA < n.

3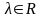 6)Собственное число и собственный столбец матрицы. Определение и основные свойства.

С обственным числом квадратной матрицы А порядка n называется такое число , для которого выполняется следующее условие:

При этом столбец называется собственным столбцом матрицы А,соответствующим собственному числу .

37)Характеристический многочлен матрицы и его свойства.

Х арактеристическим многочленом квадратной матрицы А порядка n называется следующий многочлен:

С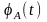 войства

1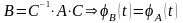 . - многочлен степени n.

2 .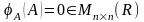

3.

38)Модель Леонтьева (модель межотраслевого баланса)

Р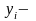 ассматривается n отраслей, каждая из которых производит свою продукцию.

П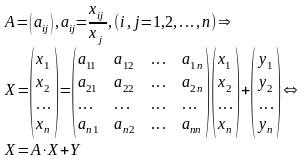 усть - общий (валовый) объем продукции i-й отрасли; объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства; объем конечного продукта i-й отрасли для непроизводственного потребления.