8. Сила давления жидкости на криволинейные поверхности. Определение горизонтальной и вертикальной составляющей. Тело давления.
Ниже рассмотрим только простейший случай криволинейной поверхности – цилиндрическую поверхность, которая встречается наиболее часто.
Обозначим через Pх и Pу горизонтальную и вертикальную составляющие силы гидростатического давления P, действующего со стороны жидкости на цилиндрическую поверхность.
1. Горизонтальная составляющая Pх искомой силы P равна силе давления жидкости на плоскую вертикальную прямоугольную фигуру, представляющую собой проекцию рассматриваемой цилиндрической поверхности на вертикальную плоскость.
2. Вертикальная составляющая Pу искомой силы P равна взятому со знаком минус весу воображаемого жидкого тела.
Это воображаемое жидкое тело называется телом давления.
Обозначив вес тела давления через G0, получаем
P0 = -G0. |
1.12 |
Если рассматриваемая цилиндрическая поверхность со стороны тела давления не смачивается жидкостью, то имеем отрицательное тело давления; в противном случае –положительное тело давления.
В случае, когда жидкость находится над цилиндрической поверхностью, вертикальная составляющая Pу будет равна
Pу = +G0. |
1.13 |
Поперечное сечение тела давления (отрицательного или положительного) представляет собой фигуру, заключенную между указанными вертикалями, самой цилиндрической поверхностью и горизонтом жидкости (или его продолжением).
9. Закон сохранения массы. Вывод уравнения неразрывности.
Уравнение неразрывности выведем из закона сохранения массы. В изолированной системе масса не меняется с течением времени, следовательно, полная производная массы по времени равна нулю.
Выделим
бесконечно малый объем жидкости 
,
масса которого 
,
и применим к нему закон сохранения массы
где 
-
проекции вектора скорости 
на
оси координат.
Раскрыв в последнем уравнении полную производную плотности по времени, получим окончательный результат
(1.2.1)
Для
несжимаемой жидкости, плотность которой
не изменяется, т.е. 
,
уравнение неразрывности примет вид:
. (1.2.2)
10. Уравнения движения идеальной несжимаемой жидкости Эйлера (без вывода). Математическая модель идеальной несжимаемой жидкости. Понятие траектории и линии тока.
Жидкость, в которой отсутствуют силы сопротивления, называется идеальной.
Уравнения движения идеальной жидкости в проекциях на координатные оси- уравнения Л.Эйлера движения невязкой несжимаемой жидкости
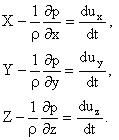
Здесь X, Y, Z — по определению, проекции ускорения массовых сил. При установившемся характере движения идеальной жидкости уравнения Эйлера могут быть проинтегрированы и приведены к виду:
или
где Ф - потенциальная функция, такая, что
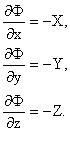
После интегрирования дифференциального уравнения при постоянстве плотности получаем
Если массовой силой является сила тяжести, то
Последнее выражение называется полным напором и обычно обозначается Н.