Угол между двумя прямыми в пространстве

За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.

Один из этих углов равен углу между направляющими векторами этих прямых.

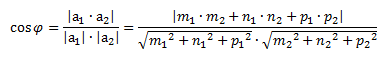
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

32. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.

Условие параллельности прямой и плоскости

Если прямая параллельна плоскости Ax + By + Cz + D = 0 , то угол между ними равен нулю, следовательно . Из формулы следует: Am + By + Cz = 0

Это и есть условие параллельности прямой и плоскости.

Условие перпендикулярности прямой и плоскости совпадает с условием параллельности этой прямой и перпендикуляра к плоскости, то есть:

33. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из данной точки на плоскость.

34. Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, опущенного из данной точки на прямую.

35. По определению, расстояние между двумя прямыми равно минимуму расстояний точек одной прямой до точек другой. Если прямые пересекаются, то этот минимум равен нулю. Если прямые параллельны, то этот минимум равен расстоянию от произвольной точки одной точки до другой прямой и может быть вычислен по формуле

36. Эллипс - это геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса , есть величина постоянная.

Каноническое ур-ие:

Оптическое свойство: оптические лучи, исходящие из фокуса эллипса, отразившись от него, проходят через второй фокус

37. Гипербола - это геометрическое место точек плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно

Каноническое ур-ие:

оптическое свойство: оптические лучи, исходящие из одного фокуса гиперболы, отразившись от нее кажутся исходящими из второго фокуса.

38.Парабола - геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы)

Каноническое ур-ие:

оптическое свойство: оптические лучи, исходящие из фокуса параболы, отразившись от нее идут параллельно ее оси.