
- •1.Вектор в геометрии — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора. Сложение
- •Векторное произведение
- •Смешанное произведение
- •9. Пучок плоскостей — уравнение любой п., проходящей через линию пересечения двух плоскостей
- •13. Цилиндрические поверхности
- •[Править]Конические поверхности
- •[Править]Поверхности вращения
- •Матричные операции
- •С помощью матрицы алгебраических дополнений
- •Метод Жордана: Алгоритм
- •Аксиомы линейного пространства
- •23. Базис. Размерность
- •Свойства нормы
- •Собственные значения и собственные векторы линейного оператора.
Свойства нормы
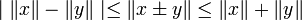
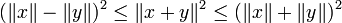
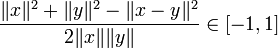 [косинус
угла]
[косинус
угла]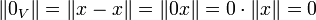
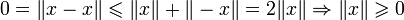 [аксиома
1]
[аксиома
1]
25.
Ортогона́льная
систе́ма элементов векторного
пространства со скалярным
произведением —
такое подмножество векторов ![]() ,
что любые различные два из них ортогональны,
то есть их скалярное
произведение равно
нулю:
,
что любые различные два из них ортогональны,
то есть их скалярное
произведение равно
нулю:
(φi,φj) = 0.
Ортогональная
система в случае её полноты может быть
использована в качестве базиса пространства.
При этом разложение любого элемента
может
быть вычислено по формулам: ![]() ,
где
,
где ![]() .
.
Любая полная линейно независимая система в конечномерном пространстве является базисом. От простого базиса, следовательно, можно перейти к ортонормированному базису.
Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространствасо скалярным произведением, обладающая свойством полноты.
Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.
Последнее удобно записывается при помощи символа Кронекера:
![]()
то
есть скалярное
произведение каждой
пары базисных векторов равно нулю, когда
они не совпадают (![]() ),
и равно единице при совпадающем индексе,
то есть когда берется скалярное
произведение любого базисного вектора
с самим собой.
),
и равно единице при совпадающем индексе,
то есть когда берется скалярное
произведение любого базисного вектора
с самим собой.
Процесс Грама (англ.)
― Шмидта —
это один из алгоритмов, в которых на
основе счётного множества линейно
независимыхвекторов ![]() строится
множество ортогональных векторов
строится
множество ортогональных векторов ![]() или ортонормированных векторов
или ортонормированных векторов ![]() ,
причём так, что каждый вектор
,
причём так, что каждый вектор ![]() или
или ![]() может
быть выражен линейной
комбинацией векторов
может
быть выражен линейной
комбинацией векторов ![]() .Алгоритм
.Алгоритм
Пусть имеются линейно независимые векторы .
Определим оператор проекции следующим образом:
![]()
где ![]() — скалярное
произведение векторов
и
.
Этот оператор проецирует
вектор
ортогонально на
вектор
.
— скалярное
произведение векторов
и
.
Этот оператор проецирует
вектор
ортогонально на
вектор
.
Классический процесс Грама — Шмидта выполняется следующим образом:
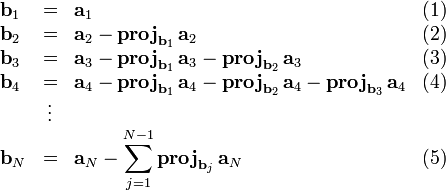
На
основе каждого вектора ![]() может
быть получен нормированный вектор:
может
быть получен нормированный вектор: ![]() (у
нормированного вектора направление
будет таким же, как у исходного, а длина —
единичной).
(у
нормированного вектора направление
будет таким же, как у исходного, а длина —
единичной).
Результаты процесса Грама — Шмидта:
— система ортогональных векторов либо
— система ортонормированных векторов.
Вычисление носит название ортогонализации Грама — Шмидта, а — ортонормализации Грама — Шмидта.
26. Лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Лине́йным отображе́нием векторного пространства LK над полем K в векторное пространство MK (лине́йным опера́тором из LK вMK) над тем же полем K называется отображение
![]() ,
,
удовлетворяющее условию линейности
f(x + y) = f(x) + f(y),
f(αx) = αf(x).
для
всех ![]() и
и ![]() .
.
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем
базис ![]() .
Пусть
.
Пусть ![]() —
произвольный вектор. Тогда его можно
разложить по этому базису:
—
произвольный вектор. Тогда его можно
разложить по этому базису:
![]() ,
,
где xk — координаты вектора в выбранном базисе.
Здесь и далее предполагается суммирование по немым индексам.
Пусть ![]() —
произвольный линейный оператор.
Подействуем им на обе стороны предыдущего
равенства, получим
—
произвольный линейный оператор.
Подействуем им на обе стороны предыдущего
равенства, получим
![]() .
.
Вектора ![]() также
разложим в выбранном базисе, получим
также
разложим в выбранном базисе, получим
![]() ,
,
где ![]() — j-я
координата k-го
вектора из
.
— j-я
координата k-го
вектора из
.
Подставим разложение в предыдущую формулу, получим
![]() .
.
Выражение ![]() ,
заключённое в скобки, есть ни что иное,
как формула умножения матрицы на столбец,
и, таким образом, матрица
при
умножении на столбец xk даёт
в результате координаты вектора
,
заключённое в скобки, есть ни что иное,
как формула умножения матрицы на столбец,
и, таким образом, матрица
при
умножении на столбец xk даёт
в результате координаты вектора ![]() ,
возникшего от действия оператора
на
вектор
,
что и требовалось получить.
,
возникшего от действия оператора
на
вектор
,
что и требовалось получить.
![]() Комментарий: Если
в полученной матрице поменять местами
пару столбцов или строк, то мы, вообще
говоря, получим уже другую матрицу,
соответствующую тому же набору базисных
элементов
.
Иными словами, порядок базисных элементов
предполагается жёстко упорядоченным.
Комментарий: Если
в полученной матрице поменять местами
пару столбцов или строк, то мы, вообще
говоря, получим уже другую матрицу,
соответствующую тому же набору базисных
элементов
.
Иными словами, порядок базисных элементов
предполагается жёстко упорядоченным.
