
- •1.Вектор в геометрии — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора. Сложение
- •Векторное произведение
- •Смешанное произведение
- •9. Пучок плоскостей — уравнение любой п., проходящей через линию пересечения двух плоскостей
- •13. Цилиндрические поверхности
- •[Править]Конические поверхности
- •[Править]Поверхности вращения
- •Матричные операции
- •С помощью матрицы алгебраических дополнений
- •Метод Жордана: Алгоритм
- •Аксиомы линейного пространства
- •23. Базис. Размерность
- •Свойства нормы
- •Собственные значения и собственные векторы линейного оператора.
Аксиомы линейного пространства
(x + y) + z = x + (y + z) (ассоциативность сложения);
x + y = y + x (коммутативность сложения);
(λμ)x = λ(μx) (ассоциативность умножения);
(λ + μ)x = λx + μx (дистрибутивность);
λ(x + y) = λx + λy (дистрибутивность);
в
 существует
такой элемент
существует
такой элемент  ,
что
,
что  для
любого
для
любого  (нулевой
элемент);
(нулевой
элемент); (умножение
на единицу);
(умножение
на единицу);
23. Базис. Размерность
Конечная сумма вида
![]()
называется линейной
комбинацией элементов ![]() с
коэффициентами
с
коэффициентами ![]() .
.
Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.
Элементы
 называются линейно
зависимыми,
если существует их нетривиальная
линейная комбинация, равная нулевому
элементу θ.
В противном случае эти элементы
называются линейно
независимыми.
называются линейно
зависимыми,
если существует их нетривиальная
линейная комбинация, равная нулевому
элементу θ.
В противном случае эти элементы
называются линейно
независимыми.Бесконечное подмножество векторов из L называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.
Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меляили линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса:
Любые n линейно независимых элементов n-мерного пространства образуют базис этого пространства.
Любой вектор
 можно
представить (единственным образом) в
виде конечной линейной комбинации
базисных элементов:
можно
представить (единственным образом) в
виде конечной линейной комбинации
базисных элементов:
![]() .
.
Конечномерное
пространство: Евклидово
пространство ![]() имеет
размерность 3, за его базис можно выбрать
тройку векторов
имеет
размерность 3, за его базис можно выбрать
тройку векторов
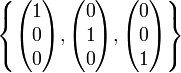
Бесконечномерное
пространство: Линейное
пространство называется бесконечномерным,
если для любого целого числа ![]() в
нем найдется линейно независимая
система, состоящая из
в
нем найдется линейно независимая
система, состоящая из ![]() векторов.
Пример:
Линейное пространство непрерывных на
сегменте функций является бесконечномерным.
Чтобы убедиться в этом, достаточно
рассмотреть степенные функции
векторов.
Пример:
Линейное пространство непрерывных на
сегменте функций является бесконечномерным.
Чтобы убедиться в этом, достаточно
рассмотреть степенные функции ![]() .
Нетрудно установить их линейную
зависимость.
.
Нетрудно установить их линейную
зависимость.
24. Евкли́дово простра́нство — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В
современном понимании, в более общем
смысле, может обозначать один из сходных
и тесно связанных объектов, определённых
ниже. Обычно n-мерное
евклидово пространство обозначается ![]() ,
хотя часто используется не вполне
приемлемое обозначение
,
хотя часто используется не вполне
приемлемое обозначение ![]() .
.
Аксиомы скалярного произведения:
(y, x) = (x, y) ;
(x + y, z) = (x, z) + (y, z) ;
(αx, y) = α(x, y) ;
(x, x)>0 x ≠ θ .
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве.
Пусть
дано линейное пространство L со
скалярным произведением ![]() .
Пусть
.
Пусть ![]() —
норма, порождённая скалярным произведением,
то есть
—
норма, порождённая скалярным произведением,
то есть ![]() .
Тогда для любых
.
Тогда для любых ![]() имеем:
имеем:
![]()
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).
![]() ,
,
в простейшем случае (евклидова норма):

где ![]() (в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
(в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
