
- •62. Простые проценты
- •Наращение по простой процентной ставке
- •Погашение задолженности частями
- •Определение срока ссуды и величины процентной ставки
- •3.2 Сложные проценты
- •Номинальная ставка
- •Эффективная ставка
- •Дисконтирование по сложной ставке процентов
- •Непрерывные наращение и дисконтирование - непрерывные проценты
- •Определение срока платежа и процентных ставок
Дисконтирование по сложной ставке процентов
Применим математическое дисконтирование по сложной ставке процента. На основе (3.16) получим:
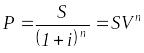 ,
(3.22)
,
(3.22)
![]() ,
(3.23)
,
(3.23)
Величину
![]() называют дисконтным
множителем.
Для случаев, когда проценты начисляются
m раз в году, получим:
называют дисконтным
множителем.
Для случаев, когда проценты начисляются
m раз в году, получим:
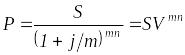 ,
(3.24)
,
(3.24)
![]() ,
(3.25)
,
(3.25)
Величину
Р , полученную дисконтированием S,
называют современной
стоимостью S. Разность
S-P , в случае когда Р определено
дисконтированием, называют дисконтом
( D ).
![]() ;
;
![]() .
.
Пример.
Сумма 5 млн. руб. выплачивается через
5 лет. Определить ее современную стоимость,
при применении ставки сложных процентов,
равных 12 % годовых. Дисконтный множитель
для данных условий составит
![]() , т.е. сумма уменьшается (дисконтируется)
почти на 44 %. Современная ее стоимость
равна:
, т.е. сумма уменьшается (дисконтируется)
почти на 44 %. Современная ее стоимость
равна:
![]() руб.
руб.
Современная величина суммы денег - одна из важнейших характеристик, применяемых в финансовом анализе.
В
практике учетных операций иногда
применяют
сложную учетную ставку. Дисконтирование
по сложной учетной ставке осуществляется
по формуле:
![]() , (3.26)
, (3.26)
где d- сложная учетная ставка.
Пример. Финансовый документ на сумму 5 млн. руб., срок платежа, по которому наступает через пять лет, продан с дисконтом по сложной учетной ставке 15 % годовых. Какова сумма дисконта?
![]()
D=S - P= 2761473,44 руб.
По аналогии с номинальной и эффективной ставкой процентов вводится понятие номинальной и эффективной учетной ставки:
![]() ,
(3.27)
,
(3.27)
где f - номинальная годовая учетная ставка.
Эффективная учетная ставка характеризует результат дисконтирования за год. Она находится из равенства
![]() ,
,
откуда
![]() .
.
Для одних и тех же условий операций эффективная учетная ставка меньше номинальной.
Пример. По данным примера, приведенного выше, определим сумму, полученную при поквартальном дисконтировании по номинальной учетной ставке 15 % (f=0,15, m=4).
![]()
Эффективная учетная ставка составит
![]() или 14,177 %.
или 14,177 %.
При использовании сложной учетной ставки:
 , (3.28) или
, (3.28) или
 , (3.29)
, (3.29)
Непрерывные наращение и дисконтирование - непрерывные проценты
В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко.
Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при обосновании и выборе инвестиционных решений, в финансовом проектировании.
При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста. Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.
При дискретном начислении процентов m раз в году по номинальной ставке j наращенная сумма определяется по уравнению:
![]()
При
![]() именем:
именем:
![]() .
.
Для
того, чтобы отличить непрерывную ставку
от дискретной, силу роста обозначают,
как
![]() , тогда:
, тогда:
![]() ,
(3.30)
,
(3.30)
Дискретные
и непрерывные ставки наращения находятся
в функциональной зависимости между
собой. Из равенства множителей наращения
![]() следует:
следует:
![]() ,
(3.31)
,
(3.31)
![]() ,
(3.32)
,
(3.32)
