
Высоцкая. Домашняя работа / Логико-математический анализ теоремы
.docxХудяков А.М. группа 9-М
Логико-математический анализ теоремы.
«Средняя линия трапеции параллельна основаниям и равна их полусумме».
(Геометрия 7-9 класс. Атанасян).
-
Теорема сформулирована в категорической форме, т. к. в тексте нет условия «если…, то…»;
-
Вид суждения: сложное (есть 2 заключения), конъюктивное (заключения связаны союзом «и»), прямое, (т. к. сначала идет условие: средняя линия трапеции, а затем заключение: параллельна основаниям и равна их полусумме), общеутвердительное (т. к. нет отрицания условной и заключительной частей);
-
Условная форма: «В любой трапеции, если есть ее средняя линия, то она параллельна основаниям и равна их полусумме»;
-
Разъяснительная часть: в любой трапеции;
-
Условие: если отрезок является средней линией трапеции;
-
Заключение: (здесь их два, структура условия и заключения - конъюктивная, т. е. соединена союзом «и») отрезок параллелен основаниям; отрезок равен полусумме оснований;
-
Обратное утверждение «Если отрезок параллелен основаниям трапеции и равен их полусумме, то он является средней линией» не является теоремой (или признаком в данном случае), т. к. без знания того, делит ли отрезок хотя бы одну из боковых сторон трапеции (потому что по т. Фалеса он с учетом параллельности основаниям, будет делить и другую посередине), нельзя будет доказать указанные в прямом суждении (см. начало) заключения.
Задача по геометрии, решаемая 5 различными способами.
B




O E D А





F C
Вначале обозначим, что AO=OD=1/2АD=2, AB=BD=CD, т. е. 2АВ=ВС, т.к. прямоугольные треугольники ABO и OBD равны по прилежащему углу и катету. По св-ву биссектрисы: AE:AB=СЕ:ВС, т.е. АЕ:СЕ=АВ:ВС=1:2, отсюда следует, что СЕ=2АЕ, а АС=3АЕ
1-й способ
Медиану
AD и биссектрису ВЕ треугольника АВС
выразим через длины сторон треугольника
АВС по формулам:

Пусть АВ = х, АЕ = у, тогда ВС = 2х, СЕ = 2у, АС=3у. Получим систему уравнений:

Отсюда x2 = 13, у2 = 5.
Ответ: АВ = √13, ВС = 2√13 и АС=3√5.
2-й способ
Обозначим угол АВЕ = ЕBD = α. По теореме косинусов из треугольников АВЕ и EBC можно выразить АЕ и СЕ:

Пользуясь тем, что СЕ = 2АЕ или CE2 = 4AE2, приравняем 1-е и 2-е уравнение. Отсюда имеем: АВ · cos α = 3 = ВО
Но x · cos α = ВО, а значит, ВО = 3, а ОЕ = ВЕ – ВО=1.
По т. Пифагора: АЕ=√АО2+ОЕ2=√5. Отсюда АС=3АЕ=3√5
По т. Пифагора: АВ=√АО2+ВО2=√13
По т. Пифагора: BD=√OD2+BO2=√13. Отсюда ВС=2BD=2√13
3-й способ
Т. к. АО = ОD = 2 и являются высотами, ВЕ-общее основание, SВАЕ = SВDE = ½ АО×ВЕ=4 (а эти треугольники равны по 2-м сторонам и углу между ними). По св-ву медианы ED делит треугольник ВEC на два равновеликих треугольника, т.е. SВАЕ = SВDE = SEDC=4. Следовательно, SАВС=3SВDE=12.
Так как AD – медиана треугольника АВС, то по св-ву медианы SABD=1/2 SABC = 6.
По формуле площади треугольника
SABD = ½ · AD · ВО = 6. Отсюда ВО=3, ОЕ= ВЕ – ВО=1.
Стороны треугольника АВС находятся по т. Пифагора (см. 2-й способ).
4-й способ
Проведем среднюю линию DF треугольника ВЕС, тогда EF=CF=AE=1/3AC.
DF || ВЕ и DF=1/2BE=2 (по св-вам сред.линии).
АО = ОD, AE=EF, следовательно, ОЕ – средняя линия треугольника АDF. Из св-ва сред.линии ОЕ = 1/2 · DF=1. Отсюда ВО=ВЕ-ОЕ=3.
Стороны треугольника АВС находятся по т. Пифагора (см. 2-й способ).
5-й способ
Секущая ВЕ пересекает стороны треугольника АСD в точках Е и О.
По теореме Менелая из треугольника АDC имеем:

ВС= 2BD и OD = AO. Следовательно 2АЕ = СЕ.
Применив теорему Менелая к треугольнику ВЕС и секущей АD, получим:
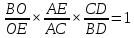
AE = 1/3AC и СD = BD. Следовательно, ВО:ОЕ = 3:1. ОЕ=1/4ВЕ=1, ВО=3ОЕ=3
Стороны треугольника АВС находятся по т. Пифагора (см. 2-й способ).
