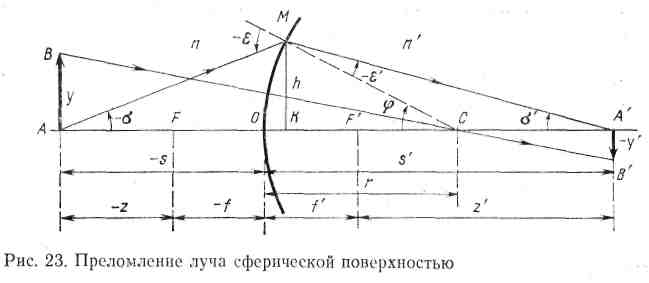
Вопрос №12 п реломление луча сферической поверхностью.

Наибольшее распространение в геодезических приборах имеют детали со сферическими преломляющими поверхно­стями.

Простейшей оптической центрированной системой является оптическая система с одной сферической преломляющей по­верхностью. На рисунке сферическая поверхность с вершиной О и радиусом r разделяет две оптически прозрачные среды с показателями преломления п и п'. Центр сферы — точка С и оптическая ось — ОС. На расстоянии s от поверхности раздела на оптической оси выберем точку А (предмет). Из этой точки проведем произвольный луч AM (в области параксиального пучка, когда до границы раздела двух сред.

Н а рисунке луч из точки А в точку М идет под малым углом к оптической оси. Лучи падающий и преломленный об­разуют с нормалью МС (радиусом кривизны сферы) соответ­ственно малые углы падения и преломления. Вы­сота точки падения М над оптической осью равна h. /По закону преломления при малых углах имеем

Для треуг.АМС угол является внешним и равен сумме внут ренних углов, не смежных с ним,

Ф ормула носит название основной формулы параксиальной оп­тики;

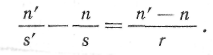
Ооптическая сила Ф системы через ее фо­кусное расстояние -

о сновное уравнение преломления луча

Придадим формуле Гаусса другой вид. -s=-f-z,

Д ля параксиального пучка s' инвариант Гюйгенса — Гельмгольца

Сферическая преломляющая поверхность характеризуется также угловым увеличением отношением углов и образованных преломленным и падающим параксиальными лучами с оптической осью,

Зависимость между угловым и линейным уве­личениями

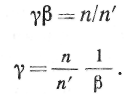
Для оптической системы в воздухе или в пустоте имеем

Продольное увеличение системы определяют по формуле

где z и z' — сопряженные отрезки на оси

Продольное увеличение систем связано с глубиной рез­кого изображения оптической системы вдоль оси.

Линейное увеличение β систем характеризует увеличение предмета в фокальной плоскости, рассматриваемое окуляром.

Видимое или окулярное увеличение Г есть отношение двух изображений на сетчатке: изображения предмета, рассматриваемого через оптическую систему, к изо­бражению того же предмета, рассматриваемого невооружен­ным глазом. Видимое увеличение можно определить как отно­шение тангенсов углов, под которыми предмет рассматривается через оптическую систему и невооруженным глазом

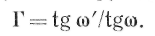
Вопрос №13 Преломление луча двумя сферическими плоскостями

Пусть на пути параксиального луча света, исходящего из точки А, расположенной на общей оптической оси С₂С_и уста­новлены две сферические поверхности с радиусами кривизны r₁ и r₂ (рис. 25). расстоянии s1', определяется формулой Аббе 1:

В точке N луч снова преломится, пойдет по направлению NА₂ и пересечет оптическую ось в точке А2/ на расстоянии S2 2:

Пренебрегая толщиной вещества — величиной d, после вы­читания из уравнения 1 уравнения 2 получим

после приведения подобных членов, имеем

Уравнение тонкой линзы (с = 0). Запишем его в виде

)

Если первой средой является воздух

(n = 1), а показатель преломления вещества линзы обозначить через п, то полу­чим в общем виде уравнение тонкой линзы:

При s=о формулу оптической силы тонкой линзы, помещенной в воздухе

-окончательный вид уравнения тонкой линзы в воздухе. Л инза является самой простой центрированной оптиче­ской системой. Она состоит из двух сферических поверхностей, ограничивающих прозрачный материал (обычно стекло). В частных случаях одна из поверхностей линзы может быть плоскостью (г = о).

Линза называется тонкой, если ее толщина d мала по срав­нению с радиусами кривизны. В тонкой линзе вершины по­верхностей совпадают с главными точками и совпадают между собой, образуя центр линзы. Линия, проведенная через центр тонкой линзы и через центры кривизны поверхностей, называ­ется оптической осью линзы. Центральную часть тонкой линзы можно принять за плоскопараллельную пластинку. Лучи, проходящие через центр линзы, практически не прелом­ляются.

Плоскости, проходящие через фокусы линзы и перпендику­лярные к оптической оси, называются фокальными плос­костями.

Для построения изображений в тонкой положительной линзе (рис. 26) достаточно провести: луч 1, падающий на пер­вую поверхность линзы параллельно оптической оси, который после преломления пересечет ось по другую сторону линзы в точке F', расположенной на расстоянии f' от линзы; затем луч 2, падающий на линзу и проходящий через ее фокус F, этот луч выходит из линзы параллельно ее оптической оси и луч 3, проходящий через оптический центр линзы, не изменяю­щий своего направления.