
- •4. Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве.
- •(Это не все свойства их очень много )
- •6.Число e
- •Сравнение бесконечно малых Отношение бесконечно малых величин образует так называемую неопределённость . [править] Определения
- •13. Признаки существования предела (сходимости)
Сравнение бесконечно малых Отношение бесконечно малых величин образует так называемую неопределённость . [править] Определения
Допустим,
у нас есть бесконечно малые при одном
и том же
![]() величины
α(x)
и β(x)
(либо, что не важно для определения,
бесконечно малые последовательности).
величины
α(x)
и β(x)
(либо, что не важно для определения,
бесконечно малые последовательности).
Если
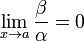 ,
то β — бесконечно малая высшего
порядка малости, чем α. Обозначают β
= o(α).
,
то β — бесконечно малая высшего
порядка малости, чем α. Обозначают β
= o(α).Если
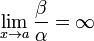 ,
то β — бесконечно малая низшего
порядка малости, чем α. Соответственно
α = o(β).
,
то β — бесконечно малая низшего
порядка малости, чем α. Соответственно
α = o(β).Если
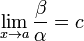 (предел
конечен и не равен 0), то α и β являются
бесконечно малыми величинами одного
порядка малости.
(предел
конечен и не равен 0), то α и β являются
бесконечно малыми величинами одного
порядка малости.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).
Если
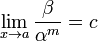 (предел
конечен и не равен 0), то бесконечно
малая величина β имеет m-й порядок
малости относительно бесконечно
малой α.
(предел
конечен и не равен 0), то бесконечно
малая величина β имеет m-й порядок
малости относительно бесконечно
малой α.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
13. Признаки существования предела (сходимости)
1. yn<=xn<=zn и Lim yn=Lim zn=C, то lim xn=c;
n->∞ n->∞ n->∞
2. последовательность монотонная и ограниченная;
3. для любого eps>0 существует такое число N=N(eps), что для всех
n>=N и m>=N |xn-xm|<eps
(критерий Коши);
14. Первым замечательным пределом называется предел
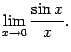
Первый
замечательный предел равен
![]()
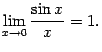
Вторым замечательным пределом называется предел
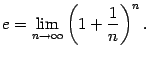
15. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
![]()
Тот
же факт можно записать иначе:
![]()
16. а практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a :
Функция f (x) определена в точке x = a;
Предел
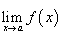 существует;
существует;Выполняется равенство
 .
.
17. Непрерывность сложной функции
Теорема . Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.
(обратной не нашёл)
18
f(x) = C, (где С – постоянная) непрерывна на R, т.к.
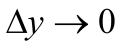 при
любом x.
при
любом x.f(x) = x, непрерывна на R, т.к.
 при
при
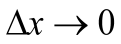 .
.f(x) =
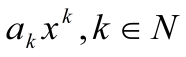 ,
непрерывна на R
как произведение непрерывных функций.
,
непрерывна на R
как произведение непрерывных функций.f(x) =
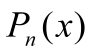 ,
непрерывна на R,
т.к. многочлен
есть
сумма непрерывных функций.
,
непрерывна на R,
т.к. многочлен
есть
сумма непрерывных функций.f(x) =
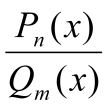 ,
где P
и Q
– многочлены степени n
и m
соответственно, непрерывна на К кроме
тех x,
при которых Q
обращается в нуль, как частное непрерывных
функций.
,
где P
и Q
– многочлены степени n
и m
соответственно, непрерывна на К кроме
тех x,
при которых Q
обращается в нуль, как частное непрерывных
функций.f(x) = sin(x), f(x) = cos(x)
Пусть
![]() –
произвольная точка множества R.
Тогда sinx-sin
–
произвольная точка множества R.
Тогда sinx-sin![]() .
Так как
.
Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]() ,
откуда следует, что функция f(x)
= sin(x)
– непрерывна.
,
откуда следует, что функция f(x)
= sin(x)
– непрерывна.
Аналогично
рассуждая, можно доказать непрерывность
косинуса. Из непрерывностей синуса и
косинуса следуют непрерывности тангенса
и котангенса, учитывая что
![]() (для
тангенса) и
(для
тангенса) и
![]() (для
котангенса).
(для
котангенса).
f(x) = arcsin(x), f(x) = arcos(x), f(x) = arctg(x), f(x) = arcctg(x) , непрерывны на своей области определения. Это следует из теоремы об обратной функции, примененной не ко всей тригонометрической функции (к примеру, sin(x)), а к ее отрезку (для sin(x) это отрезок
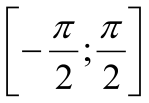 ).
). ,
где r
– рациональное. Представим r
= m
/ n,
,
где r
– рациональное. Представим r
= m
/ n,
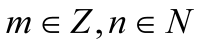 .
Тогда
.
Тогда
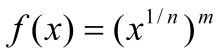 .
Функция
.
Функция
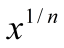 непрерывна
и строго возрастает на R.
По п. 2
непрерывна
и строго возрастает на R.
По п. 2
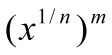 также
непрерывна.
также
непрерывна.
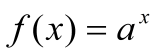 ,
a
> 1, непрерывна на R.
Пусть
–
произвольная точка множества R,
,
a
> 1, непрерывна на R.
Пусть
–
произвольная точка множества R,
 =
=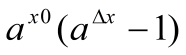 .
Докажем, что
.
Докажем, что
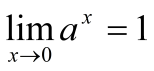 .
Пусть
.
Пусть
 -
произвольная последовательность
вещественных чисел такая, что
-
произвольная последовательность
вещественных чисел такая, что
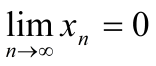 .
В силу свойств вещественных чисел
найдутся последовательности рациональных
чисел
.
В силу свойств вещественных чисел
найдутся последовательности рациональных
чисел
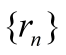 и
и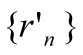 ,
удовлетворяющие при
,
удовлетворяющие при
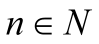 условию:
условию:
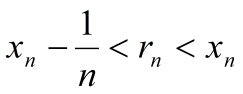 <
<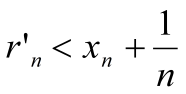 ,
откуда
,
откуда
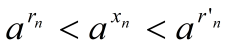 .
Так как
.
Так как
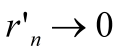 и
и
 ,
то
,
то
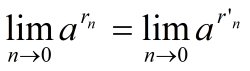 =1.
Отсюда и
=1.
Отсюда и
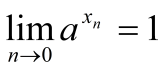 ,
ч.т.д.
,
ч.т.д.Логарифмическая функция непрерывна, что следует из непрерывности показательной функции по теореме об обратной функции.
19
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
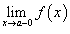 и
правосторонний предел
и
правосторонний предел
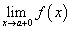 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая точка называется точкой
конечного разрыва. Модуль разности
значений односторонних пределов
![]() называется
скачком функции.
называется
скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
