
- •Предполные классы. Теорема о замкнутости предполных классов.
- •Класс функций, сохраняющих единицу: признак принадлежности к классу, доказательство замкнутости класса, мощность класса. Привести примеры элементарных булевых функций, сохраняющих единицу.
- •Лемма о нелинейной функции. Примеры применения леммы.
- •Метод резолюций в логике высказываний. Корректность и полнота метода резолюций.
- •Термы и формулы в логике предикатов. Интерпретация термов и формул.
- •Подстановка термов в формулы. Композиция подстановок. Понятие коллизии переменных.
- •Аксиоматические основания логики предикатов. Теорема универсальной конкретизации.
- •Аксиоматические основания логики предикатов. Теорема экзистенциального обобщения.
- •Доказательство общезначимости формул логики предикатов методом семантических таблиц Бета. Доказать общезначимость формулы (xU(X))(xU(X)).
- •Нормальные формы в логике предикатов. Правило построения пренексной нормальной формы. Привести к пренексной нормальной форме формулу XyU(X,y)XyB(X,y).
- •Теоретико-множественное представление -формул. Эрбрановские интерпретации. Доказательство невыполнимости предложения с использованием метода семантических деревьев. Теорема Эрбрана.
- •Исчисление предикатов как формальная система. Связь правил вывода в исчислении предикатов с аксиоматическими основаниями логики предикатов. Прямой и обратный вывод в исчислении предикатов.
Лемма о нелинейной функции. Примеры применения леммы.
Лемма
о нелинейной функции:
если
 ,
то из нее, подстановкой линейных функций
0, 1, х,
и возможно навешиванием отрицания на
саму формулу можно получить конъюнкцию
и дизъюнкцию.
,
то из нее, подстановкой линейных функций
0, 1, х,
и возможно навешиванием отрицания на
саму формулу можно получить конъюнкцию
и дизъюнкцию.
Пусть . Тогда ее полином по mod2 содержит монотонные элементарные конъюнкции ранга выше 1. Выберем среди этих элементарных конъюнкций конъюнкцию минимального ранга (>1). Для удобства рассуждений положим, что выбранная конъюнкция содержит переменные x1 и x2. Выполним следующие подстановки: всем переменным, участвующим в выбранной конъюнкции, кроме переменных x1 и x2, присвоим значение1. А всем переменным, не вошедшим в выбранную конъюнкцию, присвоим значение 0. В силу единственности полинома, представляющего данную функцию, после выполнения равносильных преобразований полином примет вид:
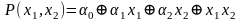 .
.
Полином
содержит три коэффициента ( )
. Каждому набору значений коэффициентов
соответствует своя собственная функция.
Следовательно, таких функций будет
восемь. Для определения всех функций,
порождаемых нелинейной функцией
заданного вида, построим таблицу.
)
. Каждому набору значений коэффициентов
соответствует своя собственная функция.
Следовательно, таких функций будет
восемь. Для определения всех функций,
порождаемых нелинейной функцией
заданного вида, построим таблицу.
-
0 1 2
Полином
Функция
000
x1x2
F(x1x2)=x1x2
001
x2x1x2=


010


011


100


101


110


111



Доказано, что из нелинейной функции могут быть получены конъюнкция и дизъюнкция.
Машина Тьюринга как пример алгоритмической системы: алгебраическое описание МТ, понятие программы, слова, конфигурации. Применимость МТ к слову. Привести пример МТ, складывающей два унарных числа.
Машина Тьюринга как пример алгоритмической системы: алгебраическое описание МТ, понятие программы, слова, конфигурации. Применимость МТ к слову. Привести пример МТ, выполняющей перевод числа из унарной системы счисления в двоичную.
Машина Тьюринга как пример алгоритмической системы: алгебраическое описание МТ, понятие программы, слова, конфигурации. Применимость МТ к слову. Привести пример МТ, переводящей числа из унарной системы счисления в троичную.
Машина Тьюринга как пример алгоритмической системы: алгебраическое описание МТ, понятие программы, слова, конфигурации. Применимость МТ к слову. Привести пример МТ, удваивающей унарные числа.
Логика высказываний как формальная модель. Основные теоремы логического вывода. Понятие семантики в логике высказываний. Доказательство выводимости формул методом семантических таблиц Бета. Корректность и полнота метода семантических таблиц.
Формулировка исчисления высказываний. Дать определения секвенции, вывода, теоремы, правила вывода, схемы аксиом. Доказательство выводимости секвенций в исчислении высказываний. Привести пример прямого и обратного доказательства выводимости секвенции |- (UU).Логическим исчислением, или просто исчислением, называется формальная система, в которой определены алфавит, правила построения формул, некоторое множество аксиом и правил вывода.Аксиомы и правила вывода позволяют строить новые формулы, которые являются общезначимыми, т.е. также являются аксиомами или теоремами. Правила вывода применяются непосредственно к формулам, а не к таблицам истинности. Исчисление высказываний может включать много аксиом и мало правил вывода, тогда оно образует формальную аксиоматическую систему или классическое исчисление высказываний. Истинность секвенции: секвенция истинна, если при любых логических значениях всех входящих в нее высказываний из истинности всех формул, входящих в левую часть секвенции, формула в правой части секвенции также становится истинной. Секвенция с пустой левой частью истинна, если правая часть тождественно истинна. Остальные секвенции назовем ложными. Любая секвенция вида Ф├ Ф, где Ф формула, истинна. Эта секвенция является единственной аксиомой исчисления секвенций. Доказательство заканчивается, когда в нижней строке записаны только аксиомы.Система аксиом логики высказываний:

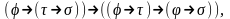









Исчисление секвенций (ИС) – это формальная система, в которой в алфавит языка логики высказываний добавлен символ следования, обозначаемый ├, который читается «выводимо» или «доказуемо».
Если U1, U2, ... , Uk , B, Gформулы , то выражения вида U1, U2, ... , Uk ├ B называются секвенциями.
Правилом вывода
называется выражение вида
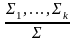 ,
где
,
где

произвольные секвенции;
называется непосредственным
следствием из
множества секвенций
по данному
правилу вывода.
произвольные секвенции;
называется непосредственным
следствием из
множества секвенций
по данному
правилу вывода.
Исчисление секвенций
определяется схемой
аксиом A├
A
и множеством правил вывода.
Аксиомой
называется выражение, получающееся из
схемы аксиом подстановкой вместо атома
A
конкретной формулы. Вывод
в ИС
это конечная последовательность
секвенций
такая, что для каждого i (1£Јi£Јk)
 есть либо аксиома, либо непосредственное
следствие из предыдущих секвенций по
правилам вывода.
есть либо аксиома, либо непосредственное
следствие из предыдущих секвенций по
правилам вывода.
Секвенция
 называется выводимой
в ИС, если
существует вывод в ИС, оканчивающийся
SS.
называется выводимой
в ИС, если
существует вывод в ИС, оканчивающийся
SS.
Правило
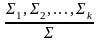 называется допустимым
в ИС, если
из выводимости
следует выводимость секвенции Σ.
называется допустимым
в ИС, если
из выводимости
следует выводимость секвенции Σ.
Введение
&:
 Удаление
&:
Удаление
&:
 Введение
:
Введение
:

Удаление
:
 Введение
:
Введение
:
 Удаление
:
Удаление
:

Введение
:
 Удаление
:
Удаление
:
 Сведение
к противоречию:
Сведение
к противоречию:
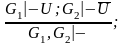
Утончение:
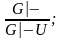 Расширение:
Расширение:

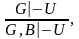 Перестановка:
Перестановка:
 Сокращение:
Сокращение:
 Сечение:
Сечение:

1. Вывести секвенцию ├ (UU).
Для доказательства истинности секвенции необходимо построить вывод, в котором доказываемая секвенция окажется последней. Начнем доказательство с аксиомы:
Σ1: U ├ U; Далее, воспользовавшись правилом (5) (введение), получаем: Σ2: ├ (UU).
