
- •Определение двойного интеграла
- •Свойства двойного интеграла
- •Приведение двойного интеграла к повторным в случае прямоугольной области
- •Приведение двойного интеграла к повторным в случае криволинейной области
- •Замена переменных в двойном интеграле
- •Вычисление двойного интеграла в полярной системе координат
- •Двойной интеграл в полярных координатах
- •Вычисление объема с помощью двойного интеграла
- •Вычисление площади поверхности с помощью двойного интеграла
- •Тройной интеграл и его свойства
- •Вычисление тройного интеграла в декартовой системе координат
- •Замена переменных в тройном интеграле
- •Вычисление тройного интеграла в цилиндрической и сферической системах координат
- •Криволинейные интегралы первого рода. Свойства
- •Вычисление криволинейных интегралов первого рода
- •Криволинейные интегралы второго рода. Свойства. Вычисление
- •Теорема Грина-Римана
- •Условие независимости криволинейного интеграла второго рода от пути интегрирования (случай плоской кривой)
- •Поверхностный интеграл первого рода. Свойства. Вычисление
- •Поверхностный интеграл второго рода. Свойства. Вычисление
- •Теорема Остроградского –Гаусса
- •Теорема Стокса (без доказательства). Условия независимости криволинейного интеграла от пути интегрирования (случай пространственной кривой)
- •Элементы теории поля
- •Множество комплексных чисел. Стереографическая проекция
- •Дифференцируемость функции комплексного переменного
- •Условия Коши-Римана
- •Интеграл от функции комплексного переменного. Свойства. Вычисление
- •Теоремы Коши для аналитической функции в односвязной области
- •Теоремы Коши для аналитической функции в многосвязной области
- •Интегральная формула Коши для аналитической функции
- •Ряд Тейлора аналитической функции
- •Изолированные особые точки аналитической функции
- •Вычет в изолированной особой точке
- •Вычисление вычетов в изолированной особой точке
- •Основная теорема о вычетах
- •Ортогональность тригонометрической системы функций
- •Ряд Фурье по тригонометрической системе функций . Теорема Дирихле
- •Тригонометрический ряд Фурье для четных и нечетных функций
- •Тригонометрический ряд Фурье в комплексной форме
- •Прямое и обратное преобразование Фурье
Определение двойного интеграла
Рассмотрим
в плоскости Оху замкнутую область D,
ограниченную линией Г, являющейся
замкнутой непрерывной кривой. z
= l(P)
= f(x,y),
P=
(x,y)
D
– произвольные ф-ции определенные и
ограниченные на D.
Диаметром области D
наз. наибольшее расстояние между
граничными точками. Область D
разбивается на n
частых областей D1…Dn
конечным числом произв. кривых. Если S
– площадь D,
то Si
– площадь каждой частной области.
Наибольший из диаметров областей обозн
.
В каждой частной области Di
возьмем произв. точку Pi
(i
, Di)
Di,
наз. промежуточной. Если диаметр разбиения
D
0 , то число n
областей Di
.
Вычислим зн-ие ф-ции в промежуточных
точках и составим сумму:I
=
 f(i,
Di)Si
(1), наз. интегральной суммой ф-ции. Ф-ция
f(x,y)
наз. интегрируемой в области D
если существует конечный предел
интегральной суммы.
f(i,
Di)Si
(1), наз. интегральной суммой ф-ции. Ф-ция
f(x,y)
наз. интегрируемой в области D
если существует конечный предел
интегральной суммы.
Двойным интегралом ф-ии f(x,y) по области D наз. предел интегральной суммы при 0. Обозн:
 или
или
Свойства двойного интеграла
1. Двойной интеграл по области D = площади этой области.
2. Если область G содержится в Д, а ф-ция ограничена и интегрируема в Д, то она интегрируема и в G.
3.
Аддитивное св-во. Если область Д при
помощи кривой г разбивают на 2 области
Д1 и Д2, не имеющих общих внутренних
точек, то:

4. константы выносятся за знак интеграла, а сумму в ф-ции можно представить в виде суммы интегралов:

5. Если ф-ции f и g интегрируемы в Д, то их произведение также интегрируемо в Д. Если g(x,y) 0 то и f/g интегрируема в Д.
6. Если f(x,y) и g(x,y) интегрируемы в Д и всюду в этой области f(x,y) <= g(x,y), то:

В частности: g(x,y) >=0 то и

7. Оценка абсолютной величины интеграла: если f(x,y) интегрируема в Д, то и |f(x,y)| интегрир. в Д причем

обратное утверждение неверно, итз интегрируемости |f| не следует интегрируемость f.
8. Теорема о среднем значении.
Если ф-ция f(x,y) интегр. в Д., то в этой области найдется такая точка (, ) Д, что:
 (2),
где S
– площадь фигуры Д. Значение f(,
)
опред по ф-ле (2) наз. средним значением
ф-ции f
по области Д.
(2),
где S
– площадь фигуры Д. Значение f(,
)
опред по ф-ле (2) наз. средним значением
ф-ции f
по области Д.
Приведение двойного интеграла к повторным в случае прямоугольной области
Приведение двойного интеграла к повторным в случае криволинейной области
Замена переменных в двойном интеграле
Для
вычисления двойного интеграла ![]() иногда
удобнее перейти в другую систему
координат.
Это
может быть обусловлено формой области
интегрирования или сложностью
подынтегральной функции.
В
новой системе координат вычисление
двойного интеграла значительно
упрощается.
Замена
переменных в двойном интеграле описывается
формулой
иногда
удобнее перейти в другую систему
координат.
Это
может быть обусловлено формой области
интегрирования или сложностью
подынтегральной функции.
В
новой системе координат вычисление
двойного интеграла значительно
упрощается.
Замена
переменных в двойном интеграле описывается
формулой
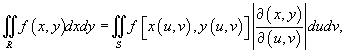
где
выражение  представляет
собой так называемый якобиан преобразования
представляет
собой так называемый якобиан преобразования ![]() ,
а S − образ области
интегрирования R,
который можно найти с помощью
подстановки
,
а S − образ области
интегрирования R,
который можно найти с помощью
подстановки ![]() в
определение области R.
Отметим, что в приведенной выше
формуле
в
определение области R.
Отметим, что в приведенной выше
формуле  означает
абсолютное значение соответствующего
определителя.
Предполагая,
что преобразование координат
является
взаимно-однозначным, обратное соотношение
описывается якобианом
означает
абсолютное значение соответствующего
определителя.
Предполагая,
что преобразование координат
является
взаимно-однозначным, обратное соотношение
описывается якобианом

при условии, что знаменатель нигде не равен 0. Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:
Найти образ S в новой системе координат
 для
исходной области интегрирования R;
для
исходной области интегрирования R;
Вычислить якобиан преобразования и записать дифференциал в новых переменных
 ;
;
Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки
 и
и 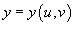 .
.
