Лабораторные работы по колебаниям и волнам

Лабораторная работа №3

ИЗУЧЕНИЕ ТЕОРИИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА

Цель работы

Задачей данной работы является ознакомление с простей-шим случаем затухающих колебаний пружинного маятника

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

• набор пружин и грузов

• измерительная установка для отсчета отклонений грузов

• секундомер

МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

П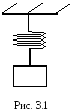 ружинный маятник – это грузик, подвешенный на пру-жине (рис. 3.1). После отклонения от положения равновесия он будет совершать вертикальные гармонические колеба-ния, если упругая пружина такова, что сила деформации пропорциональна величине удлинения пружины (, где – коэффициент упругости).

Колебания грузика описываются уравнением:

. (3.1)

Это – дифференциальное уравнение собственных незату-хающих колебаний с частотой:

.

Е сли в колеблющейся системе действуют диссипативные силы типа сил трения, пропорциональные скорости, то ко-лебания системы будут затухающими (рис. 3.2).

Уравнение колебаний будет иметь вид:

, (3.2)

где – коэффициент затухания колебаний.

Решение дифференциального уравнения (3.2) имеет вид:

. (3.3)

Из выражения (3.3) видно, что амплитуда колебаний уменьшается со временем по закону:

. (3.4)

Период затухающих колебаний больше периода собст-венных незатухающих колебаний:

, (3.5)

. (3.6)

Затухание колебаний принято характеризовать логариф-мическим декрементом затухания:

. (3.7)

Учитывая, что ,

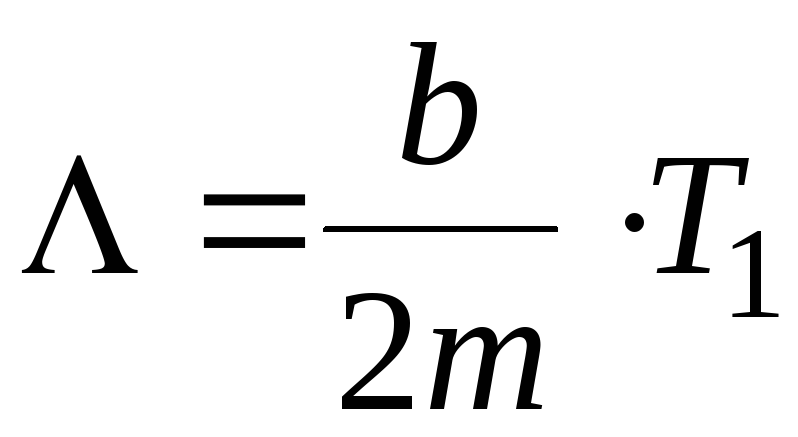. (3.8)

Пусть будет отклонение, которое имеет место через время , т.е. через колебаний после отклонения . Тогда можно записать:

,

откуда

,

(3.9)

Для пружинного маятника, колеблющегося в воздухе, ве-личина логарифмического декремента лежит в пределах от 0,01 до 0,1. Из теории затухающих колебаний следует, что вид имеет вид прямой. Здесь – амплитуда колебания.

Энергия колебательного движения изменяется по закону

, (3.10)

где – постоянная времени затухания (время релаксации), показывающая, что амплитуда колебания уменьшается за время в раз. – величина, обратная коэффициенту затухания .

Из (3.10) видно, что энергия осциллятора расходуется на работу против диссипативных сил и превращается во внут-реннюю энергию.

Мощность потерь, т.е. скорость рассеяния энергии, с од-ной стороны,

,

а с другой, с учетом (3.10),

. (3.11)

Качество колебательной системы, ее способность сохра-нять запасенную энергию характеризуется добротностью Q, которая определяется отношением запасенной энергии к потерям за время

. (3.12)

C учетом (3.11) выражение для добротности принимает вид:

. (3.13)

Из (3.13) следует, что добротность колебательной сис-темы равна числу колебаний за время ; причем за это время амплитуда уменьшается в раза, а энергия в раз.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

Упражнение 1

1.Эксперимент проводят по схеме рис. 3.1.

2. Несколько раз (4-5) измерить время , за которое гру-зик совершит колебаний. Полученные значения занести в таблицу 1. Вычислить средний период затухаю-щих колебания по формуле:

.

Вычислить среднее значение периода , абсолютную и относительную ошибку измерений. Результат занести в таблицу 1.

Таблица 1

Определение среднего значения периода

№ пп	Число колебаний	Время колебаний	Период колебаний
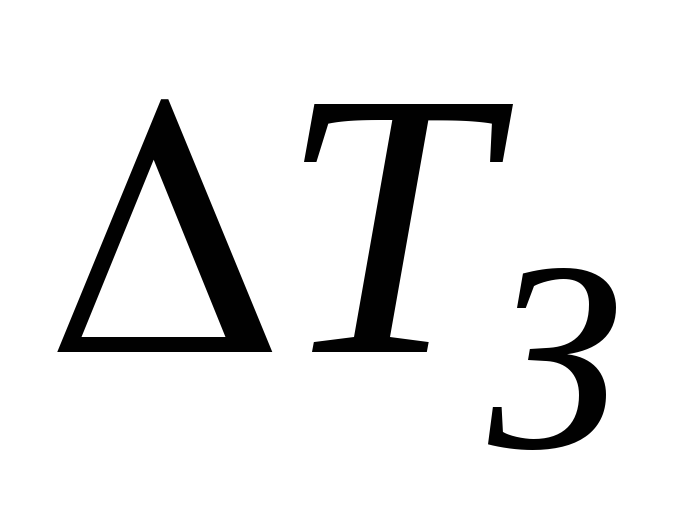
1
2
…
5

Упражнение 2

3. Установить первоначальное значение амплитуды (наибольшее отклонение от положения равновесия) око-ло 5 см. Отпустив грузик, одновременно измерить время и число полных колебаний , за которое амплитуда умень-шится на 50% от первоначальной величины: . Провести данный опыт не менее 5 раз при одном и том же значении . Полученные значения занести в таблицу 2. Вычислить средние значения и , Результат занести в таблицу 2.

Таблица 2

№ пп	Число колебаний	Время колебаний
1
2
…
5

4. Вычислить значение коэффициента затухания:

и его абсолютную ошибку

,

где – относительная ошибка .

5. Вычислить коэффициент сопротивления:

и его абсолютную ошибку

6. Рассчитать время релаксации:

и его абсолютную ошибку

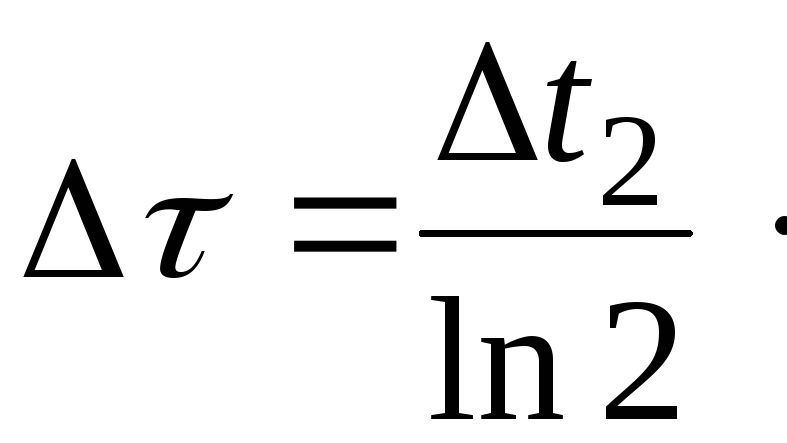
7. Рассчитать значение логарифмического декремента затухания:

и его абсолютную ошибку

где – относительная ошибка .

8. Вычислить теоретическое значение логарифмического декремента затухания

,

взяв значение из п.2, а значение – из п.4.

Найти относительную ошибку

где и – относительные ошибки и .

Рассчитать абсолютную ошибку

Сравнить теоретическое и экспериментальное значение логарифмического декремента из пп.7,8 с учетом ошибок измерений и сделать вывод.

9. Вычислить значение добротности:

используя значение из п.2, а – из п.4.

Рассчитать относительную ошибку добротности, исполь-зуя относительные ошибки и :

и абсолютную ошибку

.

Упражнение 3

10. Одеть на грузик пластину для увеличения сопротив-ления воздуха. Схема эксперимента представлена на рис. 3.3. Повторить пп. 3-9. Результаты занести в таблицу 3, анало-гичную таблице 2. Сравнить полученные значения коэффи-циента затухания и логарифмического декремента , сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Оцените относительную ошибку в определении .

2. Сформулируйте основное предположение метода наи-меньших квадратов (МНК), используйте МНК при постро-ении графиков.

3. Начертите график Т²=f(m) по МНК.

4. Оцените абсолютную и относительную ошибку при из-мерении массы.

5. Оцените абсолютную и относительную ошибку в опре-делении (наклона прямой).

6. Начертите график Т²=f(m) по МНК.

7. Найдите по графику среднее значение К.

8. Оцените, совпадают ли и с какой точностью значения К_i, полученные по графику и рассчитанные в упражнении 1.

9. Объясните, почему не рекомендуется брать большие зна-чения начальной амплитуды А₀?

10. Оцените относительную погрешность измерения А₀ и А(t),

11. Оцените относительную погрешность определения ло-гарифмического декремента затухания

12. Оцените относительную погрешность определения ко-эффициента сопротивления b.

13. Оцените абсолютную и относительную погрешность определения периода (в упражнении 1) .

14. Выведите уравнение для энергии затухающих колеба-ний в зависимости от времени, нарисуйте график.

15. Объясните, что характеризует время релаксации (пос-тоянная времени затухания).

16. Оцените мощность потерь энергии.

17. Укажите, как связаны добротность и время релакса-ции.

18. Выведите уравнение затухающих колебаний?

19. Чем определяется период затухающих колебаний?

20. Как зависит от времени амплитуда затухающих ко-лебаний?

21. Как связан логарифмический декремент затухания и амплитуда колебаний?

22. Как связан логарифмический декремент затухания с коэффициентом сопротивления и периодом?

23. Выведите выражение для энергии затухающих коле-баний.

24. Как связаны потери энергии и добротность?

25. Определите выражение для добротности контура.

26. Как связаны добротность и логарифмический декре-мент затухания?

27. Определите время релаксации. Свяжите его с коэф-фициентом сопротивления и логарифмическим декремен-том.

28. Какими являются колебания в данной работе – зату-хающими или незатухающими?

29. При каком значении коэффициента сопротивления ко-лебания прекращаются?

30. Чем отличаются колебания пружинного маятника в го-ризонтальной и вертикальной плоскости?

9

©МАТИ, 2005