Лабораторные работы по колебаниям и волнам

Лабораторная работа №5

ИССЛЕДОВАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

И ИЗУЧЕНИЕ СЛОЖЕНИЯ КОЛЕБАНИЙ С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

ЦЕЛЬ РАБОТЫ

Изучение гармонических электрических колебаний. Ис-следование сложения колебаний. Приобретение экспери-ментальных навыков исследования электрических процес-сов с помощью электронного осциллографа.

ТеоретическИе ОСНОВЫ РАБОТЫ

Рассмотрим точку, колеблющуюся с одинаковыми час-тотами во взаимно перпендикулярных направлениях. Пусть координаты иколеблющейся частицы изменяются по закону

,

(5.1)

.

Получим уравнение, описывающее поведение колеблю-щейся частицы. С учетом того, что разность фаз склады-ваемых колебаний , выражение (5.1) можно пред-ставить в виде

,

(5.2)

.

Выясним, какой вид имеет зависимость между коорди-натами ипри таких колебаниях. Выразими

через отношение амплитуд и координат.

Из (5.2) получаем:

(5.3)

(5.4)

Представим в эквивалентном виде:

(5.5)

Выражение для получим из (5.3):

. (5.6)

Подставим в (5.5) уравнения (5.3) и (5.6):

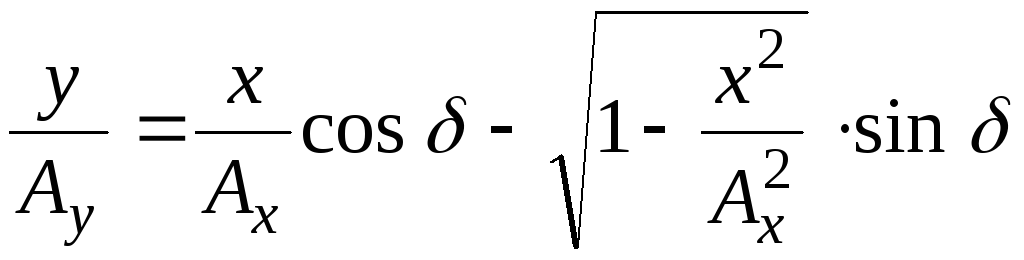. (5.7)

Перенося слагаемые из правой части в левую, получим:

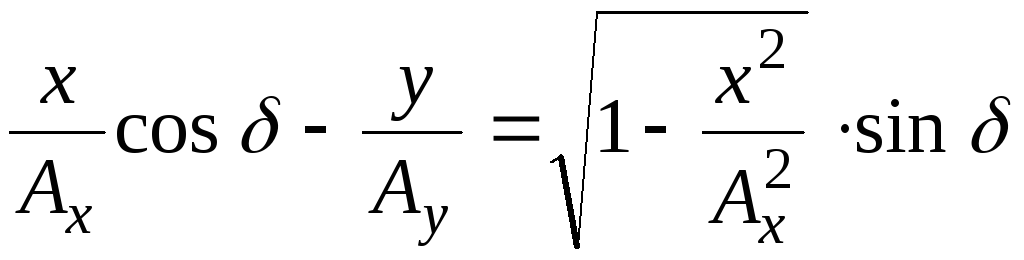. (5.8)

Возведем в квадрат:

Преобразуем полученное выражение:

Окончательно получаем уравнение движения частицы:

(5.9)

Очевидно, что в рассматриваемом случае траекторией частицы будет являться эллипс, вид которого определяется разностью фаз и отношением амплитуди(рис. 5.1).

Рассмотрим некоторые частные случаи.

1. . В этом случае,. Уравнение ко-лебания принимает вид

,

частица движется по прямой в первом и третьем квадрантах (рис. 5.2,а).

2. . При такой разности фаз,. С учетом знака уравнение колебания тоже описывает прямую

,

но частица движется по прямой уже во втором и четвертом квадрантах (рис. 5.2,б).

3. . В этом случае уравнение колебания принимает вид

,

частица движется по эллипсу, полуоси которого исовпадают с осями координат. При=эллипс превра-щается в окружность. Движение частицы по траектории бу-дет происходить в направлении часовой стрелки (рис. 5.2,в).

4. . То же самое, что и, так как изменение фазы нанесущественно. Движение будет происходить по эллипсу, как и в случае 3, с той только разницей, что движение будет осуществляться против часовой стрелки.

Если частоты взаимно перпендикулярных колебаний не одинаковы и соотносятся как целые числа, то траектория результирующего колебания имеет более сложную форму и носит название фигуры Лиссажу.

На рис. 5.3 показана фигура Лиссажу для соотношения частот . Фигуры Лиссажу для других соотношений частот представлены на рис. 5.8.

Фигуры Лиссажу очень удобно наблюдать на экране ос-циллографа, так как в этом случае можно рассматривать траектории, получающиеся при сложении колебаний, час-тоты которых соотносятся не как целые числа. Фигуры Лис-сажу при этом вращаются.

Полная энергия при сложении колебаний складывается из энергий каждого колебания:

,

или

. (5.10)

Описание установки

Лабораторная установка состоит из генератора низкочас-тотных колебаний (ЗГ), фазовращателя и электронного ос-циллографа (ЭО). При определении параметров периоди-ческого сигнала, а также исследовании сдвига фаз между двумя сигналами одной частоты используются соответст-венно одноканальный и двухканальный режимы осцилло-графа. При изучении фигур Лиссажу, которые возникают в результате сложения взаимно перпендикулярных колебаний с разными, но кратными частотами, используются оба ка-нала осциллографа. Для выполнения каждого опыта комму-тируется определенная схема экспериментальной установки.