Методички (для лаб) + некоторые решения / ТЕРМОДИНАМИКА / Молекулярная физика, процессы переноса

Лабораторные работы по молекулярной физике и термодинамике

ПРОЦЕССЫ ПЕРЕНОСА

ОБЩИЕ СВЕДЕНИЯ

Когда макросистема находится в равновесии, все ее тер-модинамические параметры постоянны по всему объему сис-темы. Если систему вывести из равновесия и предоставить самой себе, то она постепенно вернется в равновесное сос-тояние. При этом в системе будут протекать необратимые процессы, называемые процессами переноса. Различают нес-колько процессов переноса в зависимости от того, какие па-раметры системы были выведены из равновесия. Это – процессы переноса энергии, плотности и импульса, и свя-занные с ними явления теплопроводности, диффузии и вяз-кости. Процессы переноса возникают, когда имеется гради-ент какого-либо параметра макросистемы по всему объему макросистемы. При этом возникают потоки параметра в сто-рону уменьшения параметра.

Установление равновесия термодинамических систем происходит при помощи движения молекул. Это позволяет получить общее уравнение для всех явлений переноса.

Пусть имеется термодинамическая система с концен-трацией молекул, равной . Средняя скорость молекул . Движение молекул в такой системе будем считать полнос-тью хаотическим для того, чтобы не было направленных то-ков молекул и процессы переноса обусловливались только движением молекул. Возьмем некую площадку единич-ной площади. Определим плотность потока молекул, пере-секающих площадку в одном направлении. Пусть пло-щадка располагается перпендикулярно оси . Плотность потока молекул, пересекающих площадку в положитель-ном направлении оси будет

. (2.1)

Этот поток и будет переносить физическую величину , выведенную из равновесия, в сторону уменьшения ее значе-ния. Плотность потока величины обозначим как . Предположим, что величина характеризует какое-то мо-лекулярное свойство одной молекулы, причем молекула об-ладала этим свойством на расстоянии свободного пробега от площадки . То есть последнее со-ударение молекула испытывала на расстоянии от площадки .

Пусть величина изменяется вдоль оси , т.е. имеет место градиент . Тогда возникает поток величины в сторону ее уменьшения (рис.2.1).

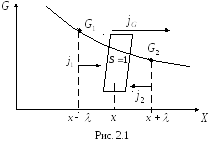
Тогда общее уравнение переноса для любой величины через площадку единичной площади, перпендикулярную на-правлению переноса, будет следующим:

, (2.2)

где – концентрация молекул,

– средняя скорость молекул,

– расстояние свободного пробега.

Значения этих величин берутся в сечении . Теперь на основе общего уравнения переноса получим уравнения для переноса массы, импульса и энергии.

Процесс переноса массы

Процесс переноса массы обусловливает явление диффу-зии. Диффузия – это самопроизвольное выравнивание кон-центраций в смеси нескольких различных веществ. Такое выравнивание концентраций происходит из-за теплового хаотического движения молекул. Рассмотрим смесь двух га-зов при постоянной температуре и давлении во всем объеме сосуда. При этих условиях не будет газодинамических по-токов, взаимопроникновение молекул будет обусловлено только тепловым движением. Суммарная концентрация обеих компонент не изменяется в зависимости от коорди-наты по оси . От координаты зависят концентрации обеих смесей ( и ). 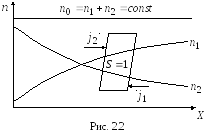То есть возникает градиент концен-трации одной из компонент, что служит причиной возник-новения процесса переноса массы каждой компоненты в на-правлении уменьшения ее концентрации (рис. 2.2).

Переносимой величиной будет являться концентрация молекул одной из компонент:

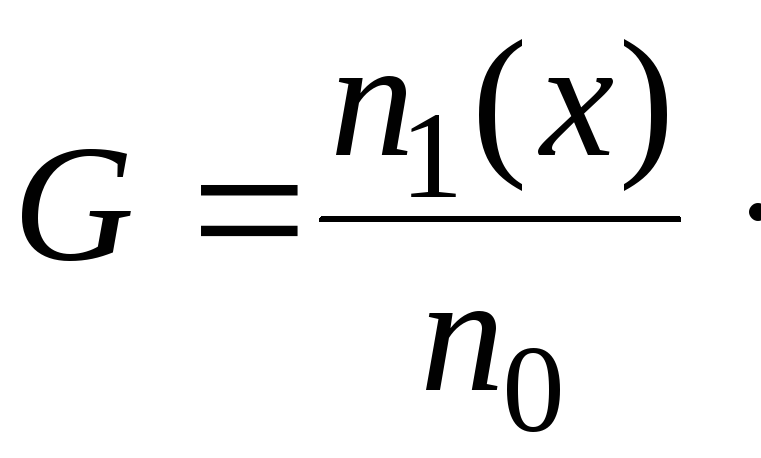(2.3)

Получаем выражения для потока этой величины:

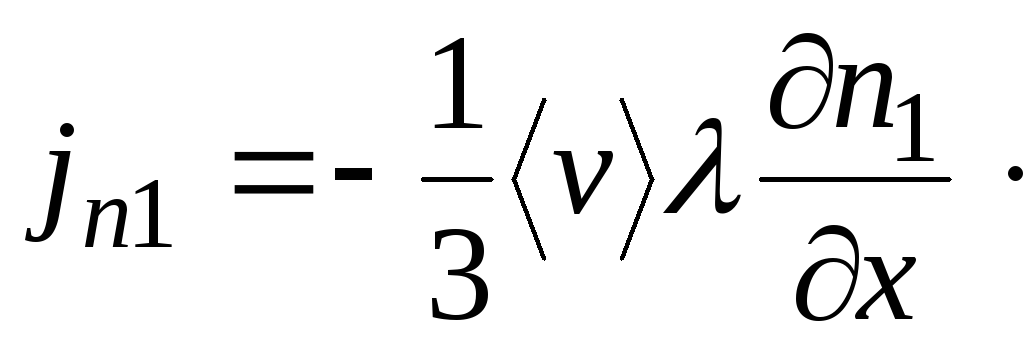(2.4)

В случае, когда смесь состоит из большего количества компонент, поток -й компоненты будет выражаться тем же соотношением:

, (2.5)

где

(2.6)

– коэффициент диффузии.

Мы получили выражение для потока через единичную площадку. При определении потока через площадку , по-лучаем соотношение, описывающее поток молекул -й ком-поненты:

. (2.7)

Из этого соотношения можем получить выражение для потока массы -й компоненты. Для этого умножим обе части уравнения на массу молекулы -й компоненты:

, (2.8)

где – парциальная плотность -й компоненты.

Два последних выражения (2.7) и (2.8) были получены эмпирическим путем и носят название закона Фика.

Размерность коэффициента диффузии – . Коэффициент диффузии определяет массу, переносимую через поверх-ность площадью за 1 секунду при градиенте плот-ности, равном . Коэффициент диффузии приближенно обратно пропорционален давлению, а при постоянном дав-лении пропорционален .

Процесс переноса импульса

Процесс переноса импульса лежит в основе явления вяз-кости или внутреннего трения. Возникает это явление в тех случаях, когда на хаотическое тепловое движение молекул накладывается упорядоченное движение молекул со скоростью . Если газ или жидкость движутся в трубе, то скорости движения различных слоев газа различны. Вследс-твие теплового движения молекулы переходят из слоя в слой, перенося с собой импульс. При этом медленные слои ускоряются, быстрые – тормозятся (рис. 2.3).

В этом случае, когда слои обмениваются импульсом, пе-реносимая величина и будет импульсом: . Плотность потока импульса через единичную площадку:

, (2.9)

где – плотность газа;

– градиент скорости в направлении оси , перпен-дикулярной направлению скорости.

На основе этого соотношения поток импульса через пло-щадку может быть рассчитан как

, (2.10)

где – динамический коэффициент вязкости.

Величина, обратная динамической вязкости, называется текучестью: .

Формула потока импульса позволяет нам получить выра-жение для силы трения между двумя слоями жидкости или газа (формула Ньютона):

. (2.11)

Размерность коэффициента вязкости – . Он численно равен силе вязкости, возникающей между слоями площадью при градиенте скорости, равном единице. Коэффи-циент вязкости определяет быстроту передачи импульса из одного слоя потока в другой. Коэффициент вязкости может быть получен из коэффициента диффузии:

(2.12)

Иногда вместо динамического коэффициента вязкости применяют кинематический коэффициент вязкости , который совпадает с коэффициентом диффузии. Вязкость газов не зависит от давления и пропорциональна . Вязкость жидкостей уменьшается с увеличением темпера-туры. Это связано с тем, что в жидкостях молекулы нахо-дятся на сравнительно небольших расстояниях друг от дру-га. Поэтому их подвижность сильно ограничена межмоле-кулярным взаимодействием. Каждая молекула находится в силовом поле, созданном соседними молекулами. Это поле можно представить в виде большой совокупности потен-циальных ям (минимумов потенциальной энергии). Потен-циальные ямы расположены друг от друга на расстояниях того же порядка, что и размеры молекул. Для того, чтобы молекула перескочила из одной потенциальной ямы в другую, она должна обладать кинетической энергией, боль-шей высоты потенциальной ямы. Поэтому коэффициент вязкости изменяется с температурой, и эта зависимость имеет вид:

, (2.13)

где – константа, слабо зависящая от температуры;

– энергия, необходимая молекуле для скачка из од-ного положения в другое, называемая энергией активации молекулы;

– постоянная Больцмана;

– абсолютная температура.

Процесс переноса энергии

Это процесс лежит в основе явления теплопроводности. Если в некоторой среде возникает градиент температуры, то возникает поток тепла. В этом случае переносимой вели-чиной будет средняя кинетическая энергия теплового дви-жения одной молекулы . Плотность потока тепла составит

. (2.14)

Переносимую величину представим в виде:

(2.15)

где – молярная теплоемкость при постоянном объеме. Отсюда получаем

. (2.16)

Умножив и разделив на массу молекулы, и учтя, что – плотность вещества и – удельная теплоемкость вещества, получаем выражение для теплового потока через единичную площадь:

(2.17)

где

(2.18)

– коэффициент теплопроводности.

Окончательно,

. (2.19)

Полученное соотношение называется законом Фурье. Теплопроводность не зависит от давления и пропорцио-нальна .

Коэффициент теплопроводности может быть получен из коэффициентов диффузии и вязкости:

. (2.20)

Коэффициент теплопроводности имеет размерность и численно равен энергии, переносимой в виде теплоты за 1 секунду через плоскую поверхность площадью при градиенте температуры, равном единице.

Общими свойствами всех трёх коэффициентов является то, что эмпирически определив , и , мы можем вы-числить длину свободного пробега и эффективный диа-метр молекул .

8

©МАТИ, 2004