Лабораторные работы по стастической физике

Лабораторная работа №2 проверка классического распределения максвелла для скоростей частиц газа термоэлектронов Цель работы

На основании опытной зависимости анодного тока электронной лампы от величины задерживающего напряжения между сеткой и катодом необходимо установить вид функции распределения по скоростям термоэлектронов, покидающих катод. Рассчитать пара-метры этого распределения. Сравнить полученную зависимость с функцией распределения Максвелла по скоростям для классичес-кого идеального газа.

Описание установки и метода исследования

Электроны, покидающие поверхность металла при термоэлект-ронной эмиссии, образуют газ электронов, совершающих беспоря-дочное тепловое движение. С известной долей приближения для их изучения можно использовать модель идеального газа. Силы вза-имодействия становятся заметными только при столкновениях, когда расстояния между частицами очень малы. При этом время столкновения гораздо меньше времени– свободного движения частиц между двумя столкновениями:.

Скорости беспорядочного теплового движения частиц газа мо-гут принимать любые значения от нуля до сколь угодно больших. При столкновениях частицы газа обмениваются скоростями, им-пульсами, энергией. Несмотря на полную хаотичность движений частиц и случайный характер столкновений и изменений их ско-ростей, распределение частиц по скоростям оказывается вполне оп-ределенным. На его характер не влияют даже внешние поля. Это распределение в случае классического идеального газа соответ-ствует теоретическому выражению, которое носит название закона Максвелла распределения молекул по скоростям:

(3.2.1)

Функция характеризует распределение по скоростям тепло-

вого движения системы, находящейся в термодинамическом равно-весии. Она определяет долю молекул единицы объема газа, скорос-ти которых заключены в интервале скоростей, равном единице, около скорости . Как следует из выражения (3.2.1), эта доля зависит от величины самой скорости, абсолютной температурыи массычастиц газа (=1.38·10Дж/К – постоянная Больц-мана). Произведениеимеет смысл вероятности обнаружения частицы со скоростью, лежащей в интервале отдо. Вид функции распределения Максвелла показан на рис.3.2.1. Поскольку в газе нет неподвижных частиц и частиц, движущихся с бесконечно большими скоростями,обращается в нуль прии.

Как видно из формы графика, наибольшая доля всех частиц дви-жется со скоростями, близкими к – наивероятнейшей скорости. Продифференцировав по скорости и приравняв полученную производную нулю, получим выражение для :

. (3.2.2)

Это значение отличается от среднего значения скорости частиц газа, которое вычисляется по формуле:

. (3.2.3)

В лабораторной работе исследуется равновесное электронное об-лако, заключенное между катодом и первой сеткой электронной лампы–пентода.

Поскольку расположение электродов в пентоде (анода, катода и трех сеток) – цилиндрическое, образуемое облако электронов, по-кидающих катод, обладает осевой симметрией. Концентрация электронов в облаке значительна, поэто-му длина их свободного пробега гораздо меньше расстояния между катодом и первой сеткой. Вылетевшие из катода электроны, многократно сталкиваясь, об-разуют газ с равномерным распределе-нием частиц по направлениям движения и с функцией распределения, имеющей характер (3.2.1). В отсутствии электри-ческого поля в лампе за пределы первой сетки могут пройти лишь электроны, ко-торые имеют радиальную составляющую, направленную к аноду; это половина всех термоэлектронов ( в пространстве скоростей это – электроны, которым со-ответствуют точки, расположенные по одну сторону от плоскости, проходящей через начало координат). Их функция распределения по скоростям содержит постоянный коэффициент, вдвое меньший, чем для функции распределения всей системы:

, (3.2.4)

здесь: – это радиальная составляющая скорости электронов в направлении от катода к аноду.

Если в пространстве между катодом и первой сеткой создается задерживающее электрическое поле, то за пределы сетки попадают только те электроны, для которых радиальная составляющая ско-рости удовлетворяет условию:

, (3.2.5)

где кг, масса электрона,Кл, величина заряда электрона,- разность потенциала катода и первой сетки.

Если практически все прошедшие первую сетку электроны дос-тигают анода, то сила анодного тока будет пропорциональна доле электронов, обладающей радиальной составляющей скорости, большей значения:

,. (3.2.6)

Определение вида функции распределения термоэлектронов ос-новано на измерении зависимости анодного тока лампы от величин задерживающего напряжения . Доля электронов в лампе, для ко-торых радиальная составляющаяскорости превышает, от чис-ла всех электронов, покидающих катод в единицу времени, опреде-ляется как определенный интеграл от, взятый в пределах отдо, что соответствует половине площади, заштрихованной на рис. 3.2.1.

, (3.2.7)

где - число всех электронов, имеющих значения скоростей, больших, т.е. число электронов, прошедших задерживающую разность потенциалов, а– число всех электронов, покидающих катод в единицу времени.

В пространстве между первой сеткой и анодом лампы создается такое ускоряющее поле, при котором все попадающие сюда элек-троны достигают анода, т.е. величина анодного тока пропорцио-нальна их числу. Если , то анодный ток насыщения. При наложении задерживающего напряжения анодный ток про-порционален :. Таким образом,

, (3.2.8)

где – некоторая сложная функция от,.

Взяв производную от членов равенства (3.2.8) по и восполь-зовавшись правилами дифференцирования интеграла и сложной функции, мы получим соотношения:

. (3.2.9)

Используя правое равенство и учитывая, что

;;,

можно записать выражение:

. (3.2.10)

Г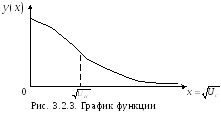рафики зависимостейи модуля производнойпоказаны на рис.3.2.3 и 3.2.4.

Определив абсциссу максимума на графике, можно рассчитать наивероятнейшую реальную скорость, воспользовав-шись соотношением (3.2.6):

. (3.2.11)

Сравнивая (3.2.11) с выражением (3.2.2), получим выражение для температуры электронного газа:

. (3.2.12)

С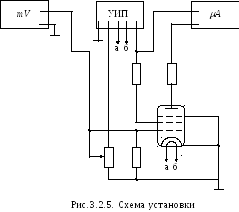хема установки показана на рис.3.2.5.

Лабораторная установка (рис. 3.3.5) функционирует следующим образом. Оператор с помощью потенциометра устанавливает раз-личные величины , фиксируя их с помощью вольтметра, и измеряет микроамперметроманодный ток. Обработка резуль-татов выполняется графическим методом. Экспериментально по-строенную зависимость назовем главной кривой.