
- •1.Кинематическое описание движения. Путь и перемещение. Скорость. Ускорение. Равноускоренное движение.
- •2. Ускорение при плоском криволинейном движении. Нормальное и тангенсальное ускорения.
- •3. Кинематика вращения твёрдого тела вокруг закреплённой оси. Угол поворота. Угловая скорость. Угловое ускорение. Связь между линейной и угловой скоростью. Равноускоренное движение.
- •4. Законы Ньютона. Принцип относительности Галилея.
- •5. Упругие силы. Силы трения.
- •6. Закон всемирного тяготения. Сила тяжести. Вес тела. Состояние невесомости.
- •7. Импульс. Импульс силы. Закон сохранения импульса. Центр масс.
- •8. Механическая работа. Мощность. Энергия. Кинетическая энергия.
- •9. Поле сил. Консервативные силы. Потенциальная энергия. Связь между потенциальной энергией и силой.
- •10. Закон сохранения полной механической энергии частицы.
- •11. Закон сохранения энергии для системы невзаимодействующих частиц.
- •12. Взаимная потенциальная энергия частиц. Закон сохранения энергии системы частиц. Потенциальная энергия тел, взаимодействующих посредством гравитационных сил.
- •13. Энергия упругой деформации. Условия равновесия механической системы.
- •14. Момент импульса. Момент силы. Потенциальная энергия. Связь между потенциальной энергией и силой.
- •15. Вращение твёрдого тела вокруг закреплённой оси. Основное уравнение динамики вращательного движения твёрдого тела.
- •16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.
- •17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
- •18. Кинетическая энергия вращающегося твёрдого тела вокруг закреплённой оси. Кинетическая энергия твёрдого тела при плоском движении.
- •19. Уравнения динамики твёрдого тела. Центр тяжести. Условия равновесия твёрдого тела.
- •20. Колебательное движение. Кинематика и динамика гармонических колебаний.
- •21. Кинетическая и потенциальная энергия гармонического колебания. Полная энергия гармонического колебания. Средние за период значения кинетической и потенциальной энергии.
- •22. Математический и физический маятники. Приведённая длина физического маятника. Центр качаний.
- •23. Сложение гармонических колебаний одного направления. Сложение взаимно перпендикулярных колебаний.
- •24. Затухающие колебания. Логарифмический декремент затухания. Добротность колебательной системы.
- •25. Вынужденные колебания. Явление резонанса. Резонансные кривые.
- •26. Основные понятия и исходные положения положения термодинамики. Обратимые и необратимые процессы. Круговые процессы (циклы).
- •27. Внутренняя энергия. Работа и теплота. Первое начало термодинамики.
- •28. Теплоёмкость. Молярная и удельная теплоёмкости. Связь между ними. Формула Майера.
- •29. Уравнение состояния идеального газа. Изотермический, изохорический и изобарический процессы и их уравнения. Графики этих процессов.
- •30. Адиабатический процесс. Уравнение Пуассона. Показатель адиабаты.
- •31. Политропические процессы. Уравнение политропы идеального газа. Показатель политропы.
- •32. Тепловые двигатели. К.П.Д. Теплового двигателя. Холодильный коэффицент. Различные формулировки второго начала термодинамики.
- •33. Цикл Карно. Первая теорема Карно. Вторая теорема Карно.
- •34. Рабочий цикл четырёхтактного двигателя внутреннего сгорания. К.П.Д. Цикла.
- •35. Рабочий цикл четырёхтактного двигателя внутреннего сгорания Дизеля. К.П.Д. Цикла.
- •36. Неравенство Клаузиуса. Равенство Клаузиуса. Энтропия. Изэнтропический процесс. Теорема Нернста(третье начало термодинамики).
- •37. Закон возрастания энтропии. Основное уравнение термодинамики.
- •38. Число степеней свободы механической системы. Поступательные, вращательные и колебательные степени свободы молекулы. Теорема о равнораспределении энергии по степеням свободы.
- •39. Классическая теория теплоёмкости идеальных газов.
- •40. Классическая теория теплоёмкости твёрдых тел (кристаллов). Закон Дюлонга и Пти.
- •41. Пространство скоростей. Функция распределения молекул по скоростям. Распределение Максвелла.
- •42. Распределение молекул по абсолютным значениям скоростей. Характерные скорости (наиболее вероятная, средняя, среднеквадратичная) в распределении Максвелла.
- •43. Барометрическая формула. Распределение Больцмана. Распределение Максвелла - Больцмана.
- •44. Энтропия и вероятность. Формула Больцмана. Макро- и микросостояния. Термодинамическая вероятность макросостояния (статистический вес).
15. Вращение твёрдого тела вокруг закреплённой оси. Основное уравнение динамики вращательного движения твёрдого тела.
Враще́ние — круговое движение объекта. В плоском пространстве объект вращается вокруг центра (или точки) вращения. В трёхмерном пространстве объект вращается вокруг линии, называемой осью. Если ось вращения расположена внутри тела, то говорят, что тело вращается само по себе или обладает спином, который имеет относительную скорость и может иметь момент импульса. Круговое движение относительно внешней точки, например, вращение Земли вокруг Солнца, называется орбитальным движением или, более точно, орбитальным вращением.
Вращение вокруг осей x, y и z называется основным вращением. Вращение вокруг произвольной оси можно рассматривать последовательно, по составляющим: сначала вращение вокруг оси x, затем как вращение вокруг оси y, и затем вращение вокруг оси z. Иначе говоря, для пространственного вращения можно сделать декомпозицию на основные составляющие.
Скорость вращения задаётся угловой частотой (рад/с), частотой (обороты/с, обороты/мин) или периодом (секунды, дни, и т.д.). Изменение во времени угловой частоты есть угловое ускорение (рад/с²), Это изменение вызывается моментом силы. Отношение двух величин момента инерции (насколько трудно начать, остановить или изменить вращение) называется моментом инерции.
В соответствии с правилом правой руки направление от наблюдателя соответствует вращению по часовой стрелке, а направление к наблюдателю — против часовой стрелки, как у винта.
Основное
уравнение динамики вращательного
движения:
![]()
16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.
Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Для
расчета моментов
инерции
тонкого диска
массы m
и радиуса R
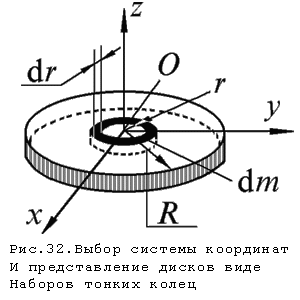
выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси z
, перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо с
внутренним радиусом r
и наружным r+dr.
Площадь такого кольца ds=2r
$\pi$ dr,
 а
его масса
а
его масса
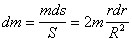 ,
где S=
$\pi$ R2
- площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом
,
где S=
$\pi$ R2
- площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом
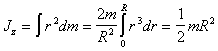
Вычисление момента инерции тонкого стержня:
Пусть
тонкий стержень имеет длину l
и массу m.
Разделим его на малые элементы длины
dx
(рис.27), масса которых
![]() .
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции
.
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции
![]() ,
т.е.
,
т.е.
![]() Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим
Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим
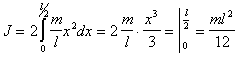
Момент
инеpции обруча
относительно оси, пpоходящей чеpез центp
кольца пеpпендикуляpно к его плоскости.
В этом случае все элементаpные массы
обруча удалены от оси на одинаковое
pасстояние, поэтому в сумме (3.18) r2 можно
вынести за знак суммы, т. е.
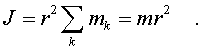
Теорема Штейнера:
В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями: J=J0+ma^2.
Например,
момент инерции диска относительно оси
О' в соответствии с теоремой Штейнера:

