29. Уравнение состояния идеального газа. Изотермический, изохорический и изобарический процессы и их уравнения. Графики этих процессов.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

•  — давление,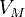

•  — молярный объём,

•  — абсолютная температура,

•  — универсальная газовая постоянная.

• уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона:

1. Изотермический процесс

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Если Т =const, то

Закон Бойля-Мариотта

Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется: p₁V₁=p₂V₂ при Т = const

График процесса, происходящего при постоянной температуре, называется изотермой.

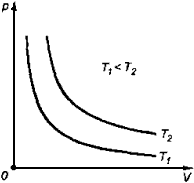
2. Изобарный процесс

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Закон Гей-Люссака

Объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре:

Если газ, имея объем V₀ находится при нормальных условиях: а затем при постоянном давлении переходит в состояние с температурой Т и объемом V, то можно записать

Обозначив

получим V=V₀ T

Коэффициент     называют температурным коэффициентом объемного расширения газов. График процесса, происходящего при постоянном давлении, называется изобарой.

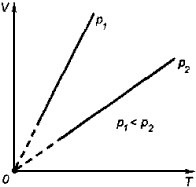
3. Изохорный процесс

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным. Ecли V = const , то

Закон Шарля

Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре:

Если газ, имея объем V₀,находится при нормальных условиях:

а затем, сохраняя объем, переходит в состояние с температурой Т и давлением р, то можно записать

График процесса, происходящего при постоянном объеме, называется изохорой.

30. Адиабатический процесс. Уравнение Пуассона. Показатель адиабаты.

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.

Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим.

Уравнение Пуассона

Для идеальных газов адиабата имеет простейший вид и определяется уравнением:

pV^k = const где:

• p — давление газа,

• V — его объём,

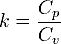• — показатель адиабаты,

• C_p и C_v — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

При адиабатическом процессе показатель адиабаты равен 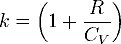где R - универсальная газовая постоянная

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду: T^kp^{1 − k} = const, где T — абсолютная температура газа.

Или к виду: Tv^{k − 1} = const

Поскольку k всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (т.е. при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов.