
Формула для определения критической силы имеет вид:
Условие
применимости формулы
Эйлера выражается
неравенством: ![]() ,
откуда
,
откуда 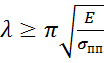 ,
где
,
где ![]() критическое напряжение,
критическое напряжение, ![]() предел пропорциональности при осевом
сжатии,
предел пропорциональности при осевом
сжатии, ![]() гибкость стержня,
гибкость стержня, ![]() коэффициент приведённой длины,
коэффициент приведённой длины, 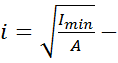 наименьший радиус инерции сечения
стержня.
наименьший радиус инерции сечения
стержня.
Для коротких стержней, до гибкости 30 – 40, критические напряжения равны: для стали – пределу текучести, для чугуна и дерева – пределу прочности.
Устойчивость за пределом упругости. Формула Ясинского:
Для
гибкостей в пределах 30![]() 40
до
40
до  были предложены различные эмпирические
формулы, показывающие, что критические
напряжения при таких гибкостях меняются
по закону, близкому к линейному.
были предложены различные эмпирические
формулы, показывающие, что критические
напряжения при таких гибкостях меняются
по закону, близкому к линейному.
Наибольшим
распространением пользуется формула
Ясинского: ![]() ,
где
,
где ![]() коэффициенты, зависящие от материала.
коэффициенты, зависящие от материала.
Проектный расчёт прочности с учётом устойчивости:
Допускаемое
напряжение на устойчивость ![]() определяется через допускаемое напряжение
на простое сжатие
определяется через допускаемое напряжение
на простое сжатие ![]() и коэффициент понижения напряжения
и коэффициент понижения напряжения
![]() ,
т.е.
,
т.е. ![]() ,
где
,
где  ,
где
,
где ![]() опасное напряжение, равное пределу
текучести
опасное напряжение, равное пределу
текучести ![]() для пластичных материалов или пределу
прочности
для пластичных материалов или пределу
прочности ![]() для хрупких материалов,
для хрупких материалов, ![]() основной коэффициент запаса прочности.
Так как
основной коэффициент запаса прочности.
Так как ![]() и
и ![]() ,
то
всегда меньше единицы.
,
то
всегда меньше единицы.
Условие устойчивости сжатого стержня:

Подбор
сечений сжатых стержней производится
путём последовательных попыток. Обычно
задаются величиной
и из выражения ![]() определяют размеры поперечного сечения.
Затем находят гибкость стержня и
соответствующую ей величину
.
Повторяют попытки до тех пор, пока
напряжение в стержне не окажется близким
к допускаемому.
определяют размеры поперечного сечения.
Затем находят гибкость стержня и
соответствующую ей величину
.
Повторяют попытки до тех пор, пока
напряжение в стержне не окажется близким
к допускаемому.
Проектный
расчёт должен быть осуществлён следующим
образом: ![]()


Расчёт прочности при изгибе с растяжением
Напряжения
в любой точке поперечного сечения при
изгибе с растяжением определяются по
формуле:  .
Отрезки, отсекаемые нейтральной осью
на главных центральных осях, равны
.
Отрезки, отсекаемые нейтральной осью
на главных центральных осях, равны 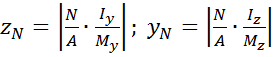 .
.
Опасными точками являются точки, наиболее удалённые от нейтральной оси.
Определение напряжений в трубопроводе при внутреннем давлении
Для
определения региональных напряжений
необходимо провести сечение перпендикулярное
оси: ![]() .
Данное выражение приближённо, т.к.
рассматривается внешний диаметр трубы.
Приближение возможно благодаря небольшой
толщине стенки
.
Данное выражение приближённо, т.к.
рассматривается внешний диаметр трубы.
Приближение возможно благодаря небольшой
толщине стенки ![]() .
.
![]()


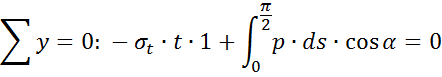
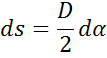

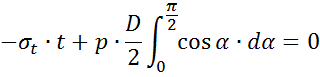


Сравнивая
выражения ![]() видим, что
видим, что ![]() .Условие
прочности:
.Условие
прочности:
![]() ,
,
![]() .
Толщина стенки:
.
Толщина стенки: .
.
