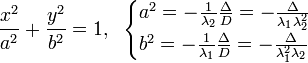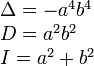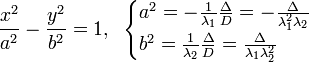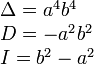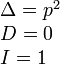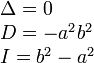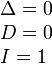Парабола

Определение. Параболой называется ГМТ плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка так, чтобы ее направление совпадало с направлением вектора . Ось Oy проведем перпендикулярно оси

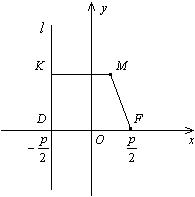
Пусть расстояние между фокусом и директрисой параболы равно p. Тогда в выбранной системе координат парабола имеет уравнение (*)

Доказательство.     В выбранной системе координат фокусом параболы служит точка , а директриса имеет уравнение

Пусть - текущая точка параболы. Тогда по формуле для плоского случая находим

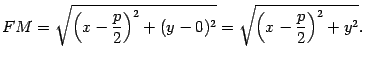
Расстоянием от точки до директрисы служит длина перпендикуляра , опущенного на директрису из точки . Из рисунка очевидно, что . Тогда по определению параболы , то есть

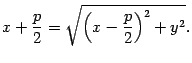
Возведем обе части последнего уравнения в квадрат:

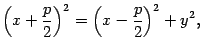
откуда

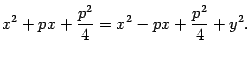
После приведения подобных членов получим уравнение (*).     

Уравнение (*) называется каноническим уравнением параболы.

Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью .

Доказательство.     Проводится так же, как и предыдущее доказательство  

Точка пересечения оси симметрии с параболой называется вершиной параболы.

Если переобозначить переменные , , то уравнение (*) можно записать в виде

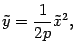
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований

Уравнение директрисы : , фокус — , таким образом начало координат  — середина отрезка . По определению параболы для любой точки , лежащей на ней выполняется равенство . и , тогда равенство приобретает вид:

.

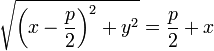После возведения в квадрат и некоторых преобразований получается равносильное уравнение .

Парабола — кривая второго порядка.

Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.

Пучок лучей параллельных оси, отражаясь в параболе собирается в её фокусе. Для параболы фокус находится в точке (0,25; 0).

Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Вид кривой	Каноническое уравнение	Инварианты
Невырожденные кривые ( )
Эллипс
Гипербола
Парабола
Вырожденные кривые (Δ = 0)
Точка
Две пересекающиеся прямые
Две параллельные прямые
Одна прямая	x2 = 0

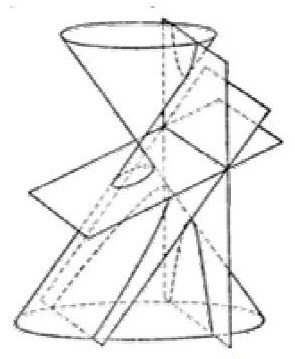
Конические сечения

Функции двух переменных

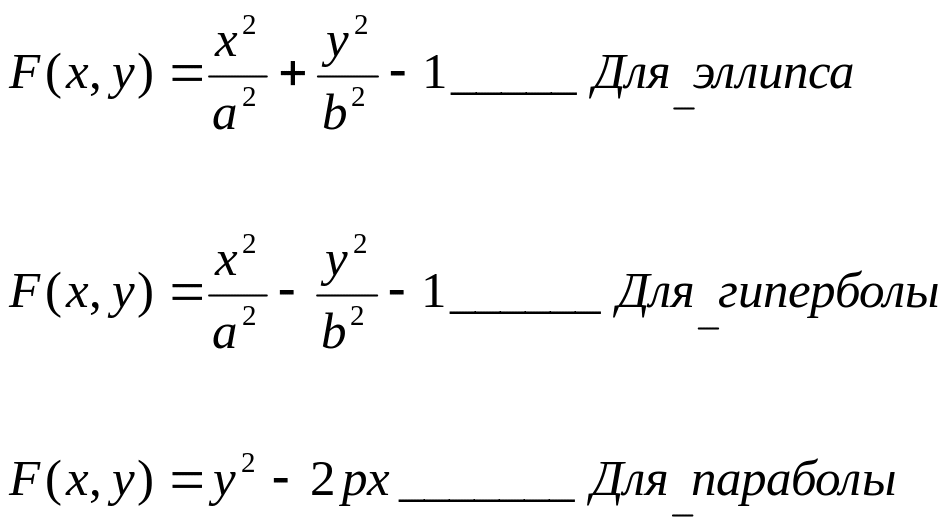
Преобразование координат

Параллельный перенос:

Пусть на плоскости заданы две декартовы прямоугольные системы координат: ("старая") и ("новая"), причем как оси абсцисс, так и оси ординат обеих систем параллельны и одинаково направлены

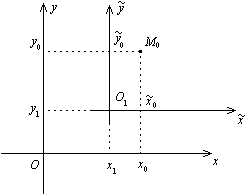<=Параллельный перенос системы координат

В этом случае говорят, что одна система координат получается из другой "параллельным переносом".

Пусть начало "новой" системы координат имеет в "старой" системе координат координаты , и пусть  - некоторая точка плоскости. Обозначим координаты точки в "старой" системе координат , а в "новой" - . Из рисунка ясно, что , .

Откуда , . Так как точка взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:

(1)

Выясним теперь, как связаны друг с другом уравнения одной и той же кривой в "старых" и "новых" координатах.

Пусть некоторая кривая задана уравнением . Тогда в системе координат , полученной параллельным переносом, с началом в точке уравнение кривой будет иметь вид .     

Однако, для практического использования это предложение удобнее сформулировать немного по-другому.

Пусть некоторая кривая задана уравнением . Тогда в системе координат , полученной параллельным переносом, с началом в точке уравнение кривой будет иметь вид .     

Доказательство обоих предложений очевидным образом следует из формул (1) связи между старыми и новыми координатами.