Взаимное расположение точки и плоскости

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.

Если точка принадлежит плоскости, то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.

Рассмотрим пример (рис.62). Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).

Задача. Дано: плоскость a(а,b) и фронтальная проекция точки А.

Требуется построить горизонтальную проекцию точки А, если известно, что она лежит в плоскости a(а,b).

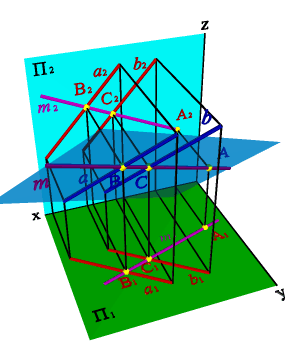
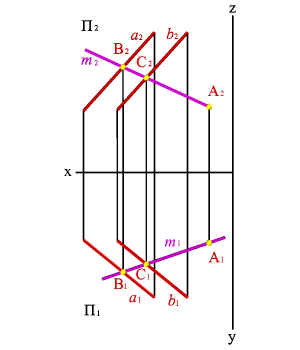
а) модель б) эпюр

Рисунок 62. Точка, принадлежащая плоскости

Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2 и b2 в точках С2 и В2 (СÎa,BÎaÞ mÎa). Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А (А1Î m1, m ÎaÞ АÎa).

Точка, лежащая в данной плоскости

Если необходимо построить некоторую точку в данной плоскости Р, то нужно предварительно провести в этой плоскости одну из прямых и на ней взять искомую точку.

Если задача обратная, т. е. необходимо узнать, лежит ли данная точка в плоскости Р, то нужно провести через эту точку какую-нибудь прямую, лежащую в этой плоскости. Если такую прямую провести нельзя, то исследуемая точка М не лежит в плоскости Р.

Часто в качестве вспомогательной прямой применяют горизонталь или фронталь, хотя можно применять и прямые общего положения.

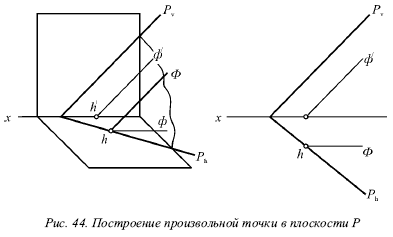
Покажем построение в плоскости Р произвольной точки (рис. 44).

Для выполнения задания необходимо провести любую горизонталь Г этой плоскости и на ней выбрать некоторую точку М. Данная точка принадлежит плоскости, следовательно, задача выполнена.