23. Угол между плоскостями. Условия параллельности и перпендикулярности Угол между плоскостями.

Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:

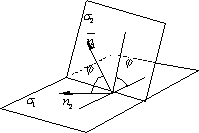
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α1 и α2 равен одному из указанных смежных двугранных углов или . Поэтому Т.к. и ,

то

Пример: Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны: или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или

Таким образом,

Примеры решений: http://examen.nx0.ru/index.php?option=com_content&view=article&id=526:2011-03-01-19-51-03&catid=13:math&Itemid=23

24. Уравнение плоскости, проходящей через 3 заданные точки

Уравнение плоскости, проходящей через три различные точки

| x - x1 y - y1 z - z1 |

| x2 - x1 y2 - y1 z2 - z1 | = 0

| x3 - x1 y3 - y1 z3 - z1 |

Если использовать векторные обозначения P1(x1,y1,z1), P2(x2,y2,z2), P3(x3,y3,z3), X(x,y,z), операцию векторного умножения двух векторов а и b как а х b = {Y1Z2 - Y2Z1, Z1X2 - Z2X1 , X1Y2-X2Y1}.Для запоминания удобно использовать запись этой формулы через определитель | i j k |

a x b = | X1 Y1 Z1 |

| X2 Y2 Z2 |

тогда уравнение плоскости можно переписать в следующем виде

((P1-P2) x (P2-P1)) . (X-P1) = 0

здесь первое умножение (х) - векторное, второе - скалярное.

Пример: Найти уравнение плоскости, проходящей через три точки P1=(0,1,1), P2=(1,2,3), P3=(-2,3,-1) векторным и обычным способом

[(0,1,1) - (1,2,3)] х [(-2,3,-1 ) - (0,1,1)] . ((x,y.z) - (0,1,2))

(-1.-1,-2) x (-2,2,-2) . (x,y-1,z-2)

(6,2,4) . (x,y-1,z-l) = 6x + 2у - 4z +2 = 0 Скалярное произведение

25. Уравнение плоскости в отрезках на осях

Уравнение 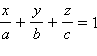называется уравнением плоскости в отрезках на осях.

Пусть плоскость пересекает координатные оси в точках (a, 0, 0) (0, b, 0) (0,0, c).

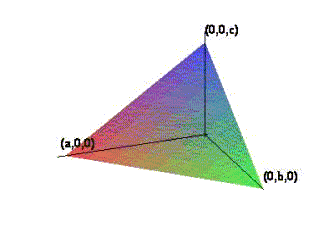
Для вывода уравнения воспользуемся уравнением плоскости, проходящей через три заданные точки:

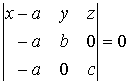
Раскрыв определитель, получим (x - a)·b·c − y·(− a·c) + z·(a·b) = 0 или x·b·c + y·a·c + z·a·b = a·b·c.

Окончательно получим уравнение плоскости в виде

Пример: Привести общее уравнение плоскости 3·x − 2·y + 5·z − 15 = 0 к виду в отрезках на осях.

Р е ш е н и е. Перенесём - 15 в правую часть и почленно разделим на это число правую и левую части данного уравнения плоскости 3·x − 2·y + 5·z = 15, ↔ ↔