16. Уравнение прямой с угловым коэффициентом

Угол α , определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k: k = tanα

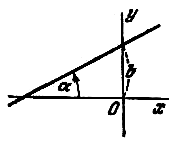
Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением: Ax + By + C = 0 , то ее угловой коэффициент определяется по формуле:

17=27.Каноническое и параметрическое уравнение прямой

Параметрические уравнения прямой

Параметрические уравнения прямой могут быть записаны в виде:

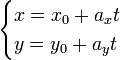
где t — производный параметр, ax, ay — координаты x и y направляющего вектора прямой, при этом

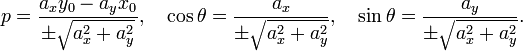
Параметр t пробегает все действительные значения.

Каноническое уравнение прямой

Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:

Вывод

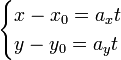
где — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.

18. Уравнение прямой, проходящей через 2 заданные точки

Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

На плоскости записанное выше уравнение прямой упрощается:

если х1 ≠ х2 и х = х1, еслих1 = х2

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Применяя записанную выше формулу, получаем:

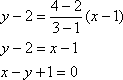
19 Копия 29(смотреть теорию в нём)

20. Уравнение прямой в отрезках на осях

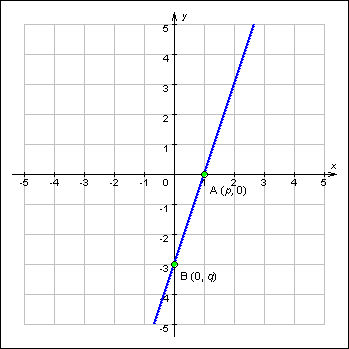
Общее уравнение прямой a x + b y = c, где a · b · c ≠ 0. Его можно преобразовать к виду 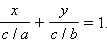Это уравнение пересекает координатные оси в точках (p; 0) и (0; q). в чем легко убедиться, подставив координаты этих точек в уравнение прямой. Полученное уравнение называется уравнением прямой в отрезках:

21. Расстояние от точки до прямой

Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от дочки до прямой.

Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:

Координаты x1 и у1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим:

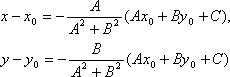
Подставляя эти выражения в уравнение (1), находим:

22. Общее уравнение плоскости

декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение

определяет плоскость, проходящую через точку и имеющей нормальный вектор

Раскрывая в уравнении (1) скобки и обозначая число буквой D, представим его в виде

Это уравнение называется общим уравнением плоскости.